B-trees, Shadowing, Clones
Ohad Rodeh
IBM Haifa Research Labs
Сам документ можно скачать тут
Бинарные деревья используются многими файловыми системами для представления файлов и каталогов.
Время поиска, вставка, удаление в таких файловых системах имеет логарифмическую зависимость.
Такие файловые системы, как WAFL или ZFS, имеют встроенный механизм shadowind, или
copy-on-write, на основе которого реализуются снэпшоты, восстановление после аварий, RAID.
Этот документ описывает набор алгоритмов, реализующих этот самый shadowing (я не знаю,
как лучше перевести это слово :) , который позволяет сделать достаточное количество снэпшотов
в фоновом режиме и при этом достигается хороший параллелизм работы самой файловой системы.
Бинарные деревья - это альтернативный алгоритм реализации файловых систем по сравнению
с традиционным юниксовым подходом (ext), использующим косвенную индексацию блоков.
Файловая система представляет из себя дерево, состоящее из страниц фиксированного размера.
Shadowing буквально означает следующее: если нам нужно модифицировать какую-то страницу из такого
дерева, мы читаем эту страницу в память, модифицируем эту копию и потом сбрасываем эту копию обратно на диск.
После этого необходимо будет тут же изменить родительскую ссылку, которая будет вести на обновленную копию.
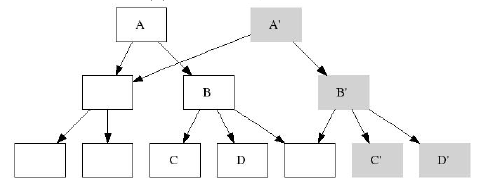
Это т.н. строгий (strict) shadowing-алгоритм: на рисунке показано, что была промодифицирована целая ветка
вплоть до корня
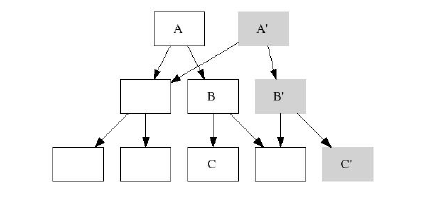
Т.е. данный алгоритм позволяет иметь для файловой системы более одного (!) рута в зависимости от количества
снэпшотов. И каждый рут будет указывать на свой собственный мгновенный снимок файловой системы.
Удалить такой рут можно только вместе со снэпшотом.
Обычно файловые системы (XFS,JFS) используют вариант бинарных деревьев, который называется b+tree.
В них ноды делятся на корневые и на листья. Корневые ноды содержат только индексные ключи,
в листьях находятся сами данные.
Основное требование, предьявляемое к бинарным деревьям - это устойчивость и восстанавливаемость.
Обновление дерева происходит снизу-вверх. Модифицируются листья. Иногда листья могут клонироваться
или наоборот обьединяться, что может вызвать рекурсивное изменение вверх.
Листья обьединяются в цепочку для балансировки самого дерева.
Основные проблемы, которые возникают при попытке сделать shadowing для классического типа деревьев:
На следующем рисунке представлена дерево с цепочкой связи между листьями.
Если мы будем стандартный copy-on-write для ноды C, у нас порвется связь в созданном снэпшоте
для ноды C.
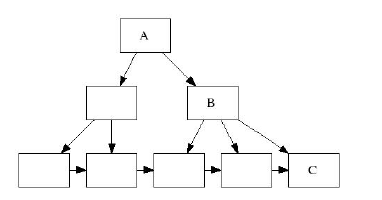
Параллелизм: в момент copy-on-write изменения листьев, происходит модификация всей ветки, вплоть до корня,
что вызывает блокировку всего дерева на момент апдэйта.
Модификация ключей: на следующем рисунке нода A имеет 2 соседних ноды - L и R.
Из ноды A удаляется ключ, при этом происходит модификация дерева(серый цвет). Если удаляемый ключ относится
к ноде L, то возникают дополнительные проблемы с модификацией дерева.
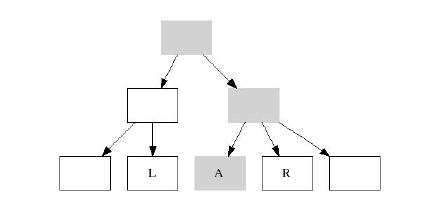
Мы изменим подход и вместо алгоритма "снизу-вверх" выберем алгоритм прохода дерева "сверху-вниз".
Также вместо цепочки связей между листьями мы будем использовать механизм обратных ссылок.
Checkpoint - моментальный снимок файловой системы на диске. Если в файловой системе происходит сбой.
то будет откат к предыдущему чек-пойнту.
Рассмотрим дерево:
На следующем рисунке серым цветом показана его модификация
На следующем рисунке картина после закомиченного чек-пойнта
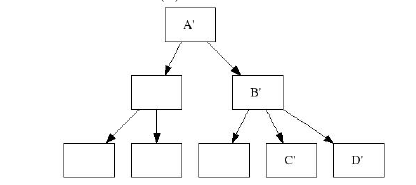
Чек-пойнты эффективны, потому что их запись происходит в пакетном режиме, и всегда можно откатиться в случае чего.
Логирование представляет дополнительные возможности в том плане, что все модификации файловой системы
логируются в одном журнале. Комбинация чек-пойнтов и логов дает эффективный механизм плюс дополнительное
кеширование дерева в памяти, при котором все модификации происходят на лету и в нужный момент сбрасываются на диск.
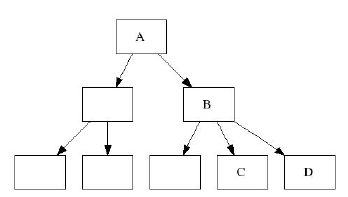
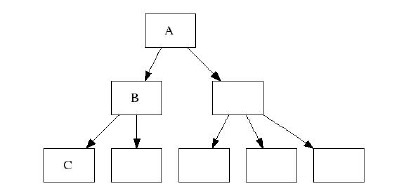
Как я уже отметил, в этой статье используются b+tree. В таких деревьях листья включают пары "ключ-данные",
а индексные ноды содержат связи между ключами и дочерними нодами. На следующем рисунке нода A - рутовая нда,
B - индексная нода, C - нода-лист. При этом между листьями нет никакой связи. Каждая нода занимает 4 килобайта
дискового пространства. Наше дерево также сбалансировано - это означает что расстояние от любого листа до рута одинаково.
Ключи работают по принципу минимума: они указывают на лист, который всегда не-меньше самого ключа:
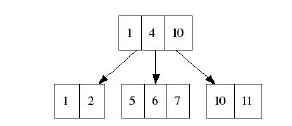
Нода может включать листья в диапазоне b и (2b + 1) для b>=2.
Если нода имеет (2b + 1) листьев, то при добавлении очередного листа она разбивается.
Если нода содержит b листьев, то при удалении листа из такой ноды она обьединяется с соседом.
Мы берем для всех примеров b=2 и диапазон [2...5].
При проходе дерева сверху вниз мы блокируем целые ветки. При добавлении-удалении ключа происходит
дублирование целых веток, это сопровождается соответствующей блокировкой, подготовительными операциями
и собственно дублированием (или shadowing), и все это происходит за один проход.
При удалении дерева используется post-order проход.
Для дерева
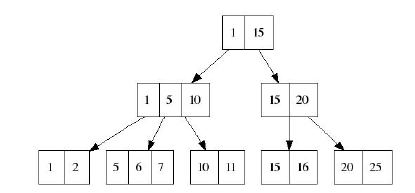
удаление будет выполнено по правилу:
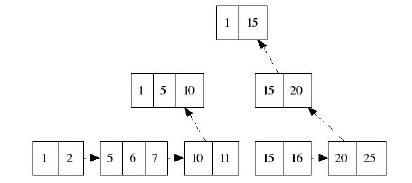
Вставка одного ключа может сопровождаться спонтанным разбиением/добавлением нод сразу на нескольких уровнях.
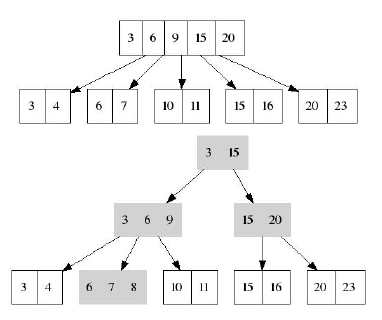
Сказанное иллюстрирует следующий рисунок: вставляется ключ 8, при этом происходит: 1) разбиение рутовой ноды
2) добавление промежуточных нод
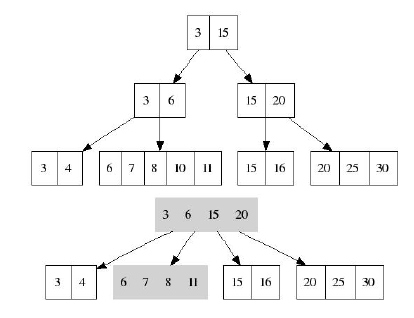
Удаление одного ключа может привести к обратным массовым модификациям всего дерева: например, удаление
ключа 3 из второго уровня:
На практике, ограничение для числа листьев находится в пределе [b,3b].
При вставке/удалении число модифицируемых дисковых страниц может быть равно (2 * глубину дерева).
Поскольку дерево сбалансировано, глубина дерева может быть, в худшем случае, логарифм от N по основанию b,
где N - число ключей в дереве.
На следующем рисунке показано клонирование дерева. Справа ноды B и C увеличивают свои ссылочные счетчики
на 1. Нет нужды в создании полной копии дерева слева - это неэффективно, просто создается еще одна корневая нода Q:
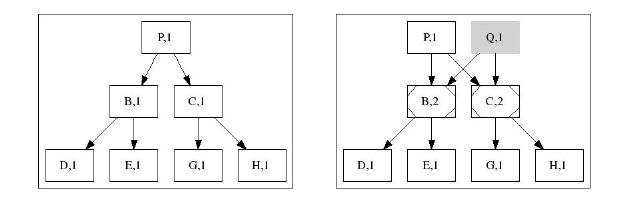
На следующем рисунке показано, как после удаления дерева Tq уменьшаются счетчики ссылок в нодах C, Y:
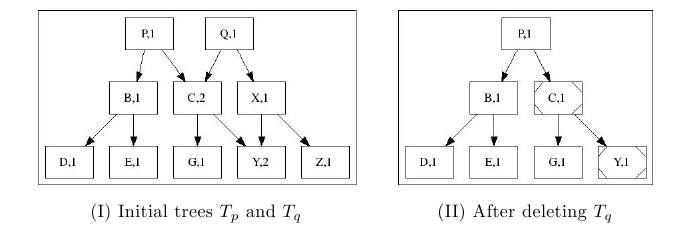
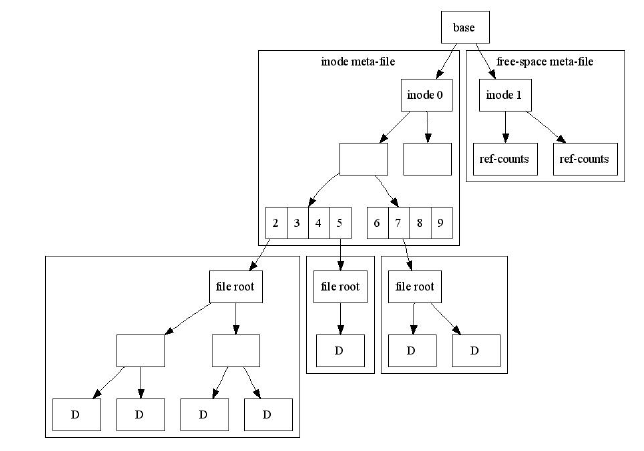
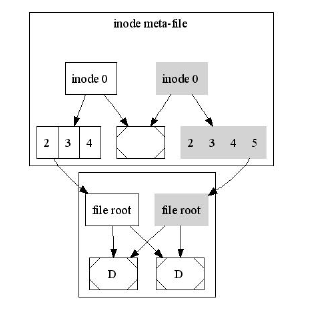
Рассмотрим пример файловой системы. Рутовая нода указывает на meta-file, хранящий дисковые ноды,
при этом каждая нода укзывает на дерево, хранящее файловые данные - в данном случае ноды 2,5, 7 имеют
такие данные. Еще один meta-file хранит свободные счетчики:
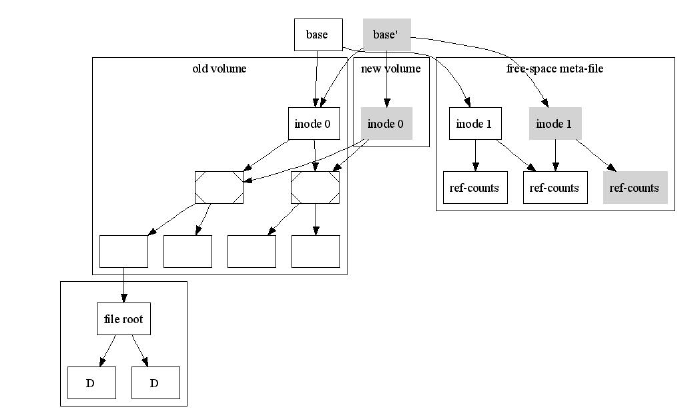
При клонировании тома происходит следующее:
При клонировании файла происходит следующее:
| 