Search     or:     and:
 LINUX 
 Language 
 Kernel 
 Package 
 Book 
 Test 
 OS 
 Forum 
iakovlev.org

Chapter 7: An Introduction to Writing Parallel Programs for Clusters

Overview

Ewing Lusk, William Gropp, and Ralph Butler

There are two common kinds of parallelism. The first, the master-worker approach, is the simplest and easiest to implement. It relies on being able to break the computation into independent tasks. A master then coordinates the solution of these independent tasks by worker processes. This kind of parallelism is discussed in detail in this Chapter, starting with Section 7.1. This part of the chapter has three goals:

  • To present some of the ways parallelism can be introduced into an application.

  • To describe how to express parallelism using functions built into the operating system. Depending on your target application, this information may be all you need, and we will show how to access these functions from several different application-development languages.

  • To provide some realistic examples of applications illustrating this approach. We include string matching with applications to computational biology.

The first task in creating a parallel program is to express concurrent work. Section 7.1 then focuses on task parallelism. Section 7.2 describes the use of Linux system calls for task parallelism. Section 7.4 then outlines an example from computational biology to illustrate the use of task parallelism to carry out a large computation.

The second kind of parallelism is for computations that cannot (or cannot easily) be broken into independent tasks. In this kind of parallelism, the computation is broken down into communicating, interdependent tasks. One example of this kind of parallelism was introduced in Section 1.3.6. These parallel programs are more difficult to write, and a number of programming models have been developed to support this kind of parallel program. The most common, and the one most appropriate for Beowulf clusters, is message passing. The two most common message-passing systems are MPI (Message Passing Interface) and PVM (Parallel Virtual Machine), covered in Chapters 8–11. In this chapter, Section 7.5 introduces some of the techniques used in dividing programs into communicating, interdependent parts. Expressing these ideas as programs is left for the following chapters.

7.1 Creating Task Parallelism

The essence of task parallelism is that the task to be accomplished can be executed in parallel. Since we assume that the tasks are not completely independent (otherwise they are just a collection of ordinary sequential jobs), some sort of coordinating mechanism must exist. We will call this process the manager, and the processes that carry out the subtasks the workers. (The manager could even be the human user, who manages the worker processes "by hand," but we will assume that the manager is a single program that the user causes to be started.) Manager/worker algorithms and execution mechanisms have many variations, which we survey in the next section; but as we use the term, "task parallelism" always involves the following steps.

  1. Divide the task into independent or nearly independent subtasks. By "independent" we mean that while communication of some sort occurs between the manager and the workers, there is no direct communication between any two workers.

  2. Start the workers. We assume that each worker is represented by an operating system process. In Section 7.2 we will describe Unix processes and how to start them. (Use of threads for workers is atypical for a Beowulf cluster and will not be described.)

  3. Communicate subtask specifications from the manager to the workers.

  4. Communicate results from the workers to the manager.

  5. Ensure that all results have been collected and that the workers have been shut down.

7.1.1 Variations on Task Parallelism

The scheme just described had many variations; we will discuss a few of them here, and then in the following section we will illustrate some of these with concrete examples. The variations involve the scheduling algorithm by which the manager assigns subtasks to the workers, the ways in which the worker processes are started and managed, and the communication mechanism between manager and workers.

Variations in How Work Is Assigned

For an efficient manager/worker parallel program, the workers should be kept working as much of the total time as possible. If the total work to be done can be easily divided into arbitrarily sized subtasks, then the scheduling job is easy: if there are n workers, then divide the work up into n pieces, each of which will take the same amount of time, and give one piece to each worker. This is called static scheduling.

Although sometimes such scheduling can be done, breaking up the total amount of work into subtasks typically results in subtasks of widely differing sizes, more subtasks than there are workers, or both. In all of these cases, the manager must organize the assignment of work to workers more carefully in order to keep the workers working. If some workers are idle when there is still more work to do, a load balancing problem occurs. Fortunately the general manager/worker algorithms can be used to overcome this problem when there are substantially more subtasks than there are workers. The idea is for the manager to make an initial assignment of subtasks to workers and then wait for subtask completion by any worker. At that point the worker can be assigned another subtask. In this way the master does not need to know ahead of time how much time each subtask will take; it just keeps all the workers as busy as possible.

Figure 7.1 shows a high-level framework for the manager and worker in a manager/worker system. In this example, n processes (workers) are started and then each process is sent the data for each task to perform. New processes are started once rather than for each task, because starting a new process is often a time-consuming operation.

Start Figure 
     manager:                             worker:
     for (i=0; i<n; i++) {                receive msg from manager
         start new process                while (not exit msg) {
         send work                            do work
     }                                        send results
     while (not done) {                       receive next message
         wait for msg from any worker     }
         receive results                  exit
         if (work left) {
             send new work to worker
         }
         else {
             send exit msg to worker
         }
     }
End Figure

Figure 7.1: Schematic of a general manager-worker system

We note a few points about this algorithm.

  • A load balancing problem will inevitably occur near the end of the job, as some workers become idle but there is no more work to be assigned, because all the work that is not done is being worked on by other workers.

  • To make this period of load imbalance as small as possible, it is a good idea to make the subtasks small. If the manager can estimate the sizes of the subtasks, then it should assign the larger tasks first and the smaller ones near the end.

  • If the subtasks are too small, then the overhead of communication between manager and worker will take up too much of the total time.

Therefore one needs to give some thought to just exactly how to divide up the work. A technique that is sometimes used is to further subdivide the work units during the computation. In some algorithms, the workers subdivide their own tasks and return the new subsubtasks to the manager for redistribution to the other workers. An example is the Mandelbrot program described in Chapter 5 of [48].

Variations in Implementation Mechanisms

Processes can be started in a variety of ways, including shell commands, Unix system calls, remote shell commands of different kinds, parallel process management systems, and the use of daemons of various kinds. Even Web browsers can be used to launch remote tasks. We will discuss process startup in Section 7.2, after we have established a deeper understanding of operating system processes.

Similarly, the communication between manager and worker can be carried out in many ways. One way is to use the file system as a communication device. This is particularly convenient if all of the workers have access to the same file system. (See Chapter 19 for a discussion of shared file systems.) This mechanism is often used when the manager is programmed as a shell script.

A more flexible and powerful approach to communication among processes uses sockets. Sockets and how to use them in several programming languages are covered in Section 7.2.5. The use of higher-level communication libraries (MPI and PVM) is covered in later chapters.

7.2 Operating System Support for Parallelism

Although parallel programs can be quite complex, many applications can be made parallel in a simple way to take advantage of the power of Beowulf clusters. In this section we describe how to write simple programs using features of the Linux operating system that you are probably already familiar with. We begin with a discussion of processes themselves (the primary unit of parallelism) and the ways they can be created in Unix environments such as Linux. A good reference on this material is [111].

7.2.1 Programs and Processes

First we review terminology. A program is a set of computer instructions. A computer fetches from its memory the instruction at the address contained in its program counter and executing that instruction. Execution of the instruction sets the program counter for the next instruction. This is the basic von Neumann model of computation. A process consists of a program, an area of computer memory called an address space, and a program counter. (If there are multiple program counters for a single address space, the process is called a multithreaded process.) Processes are isolated from one another in the sense that no single instruction from the program associated with one process can access the address space of another process. Data can be moved from the address space of one process to that of another process by methods that we will describe in this and succeeding chapters. For the sake of simplicity, we will discuss single-threaded processes here, so we may think of a process as an (address space, program, program counter) triple.

7.2.2 Local Processes

Where do processes come from? In Unix-based operating systems such as Linux, new processes are created by the fork system call. This is an efficient and lightweight mechanism that duplicates the process by copying the address space and creating a new process with the same program. The only difference between the process that executed the fork (called the parent process) and the new process (called the child process) is that the fork call returns 0 in the child and the process id in the parent. Based on this different return code from fork, the parent and child processes, now executing independently, can do different things.

One thing the child process often does is an exec system call. This call changes the program for the process, sets the program counter to the beginning of the program, and reinitializes the address space. The fork-exec combination, therefore, is the mechanism by a process create a new, completely different one. The new process is executing on the same machine and competing for CPU cycles with the original process through the process scheduler in the machine's operating system.

You have experienced this mechanism many times. When you are logged into a Unix system, you are interacting with a shell, which is just a normal Unix process that prompts you, reads your input commands, and processes them. The default program for this process is /bin/bash; but depending on the shell specified for your user name in '/etc/passwd', you may be using another shell. Whenever you run a Unix command, such as grep, the shell forks and execs the program associated with the command. The command ps shows you all the processes you are running under the current shell, including the ps process itself (strictly speaking, the process executing the ps program).

Normally, when you execute a command from the shell, the shell process waits for the child process to complete before prompting you for another command, so that only one process of yours at a time is actually executing. By "executing" we mean that it is in the list of processes that the operating system will schedule for execution according to its time-slicing algorithm. If your machine has ony one CPU, of course only one instruction from one process can be executing at a time. By time-slicing the CPU among processes, however, the illusion of simultaneously executing process on a single machine, even a single CPU, is presented.

The easiest way to cause multiple processes to be scheduled for execution at the same time is to append the '&' character to a command that you execute in the shell. When you do this, the shell starts the new process (using the fork-exec mechanism) but then immediately prompts for another command without waiting for the new one to complete. This is called "running a process in the background." Multiple background processes can be executing at the same time. This situation provides us with our first example of parallel processes.

To determine whether a file contains a specific string, you can use the Unix command grep. To look in a directory containing mail files in order to find a message about the Boyer-Moore string-matching algorithm, you can cd to that directory and do

     grep Boyer *

If your mail is divided into directories by year, you can consider search all those directories in parallel. You can use background processes to do this search in a shell script:

     !# /bin/bash
     echo searching for $1
     for i in 20* ;
         do ( cd $i; grep $1 * > $1.out & ) ;
     done
     wait
     cat 20*/$1.out > $1.all

and invoke this with Boyer as an argument.

This simple parallel program matches our definition of a manager/worker algorithm, in which the master process executes this script and the worker processes execute grep. We can compare its properties with the list in Section 7.1:

  1. The subtasks, each of which is to run grep over all the files in one directory, are independent.

  2. The workers are started by this shell script, which acts as the master.

  3. The subtask specifications (arguments to grep) are communicated to the workers on their respective command lines.

  4. The results are written to the file system, one result file in each directory.

  5. The wait causes the shell script to wait for all background processes to finish, so that the results can be collected by the manager (using cat) into one place.

One can make a few further observations about this example:

  • The first line of the script tells the system which program to use to interpret the script. Here we have used the default shell for Linux systems, called bash. Other shells may be installed on your system, such as csh, tcsh, or zsh. Each of these has a slightly different syntax and different advanced features, but for the most part they provide the same basic functionality.

  • We could have made the size of the subtask smaller by running each invocation of grep on a single file. This would have led to more parallelism, but it is of dubious value on a single machine, and we would have been creating potentially thousands of processes at once.

  • We could time this script by putting date commands at the beginning and end, or by running it under the shell's time command:

            time grepmail boyer

    where grepmail is the name of this script and boyer is the argument.

7.2.3 Remote Processes

Recall that the way a process is created on a Unix system is with the fork mechanism. Only one process is not forked by another process, namely the single init process that is the root of the tree of all processes running at any one time.

Thus, if we want to create a new process on another machine, we must contact some existing process and cause it to fork our new process for us. There are many ways to do this, but all of them use this same basic mechanism. They differ only in which program they contact to make a fork request to. The contact is usually made over a TCP socket. We describe sockets in detail in Section 7.2.5.

rsh

The rsh command contacts the rshd process if it is running on the remote machine and asks it to execute a program or script. To see the contents of the '/tmp' directory on the machine foo.bar.edu, you would do

     rsh foo.bar.edu ls /tmp

The standard input and output of the remote command are routed through the standard input and output of the rsh command, so that the output of the ls comes back to the user on the local machine. Chapter 5 describes how to set up rsh on your cluster.

ssh

The ssh (secure shell) program behaves much like rsh but has a more secure authentication mechanism based on public key encryption and encrypts all traffic between the local and remote host. It is now the most commonly used mechanism for starting remote processes. Nevertheless, rsh is substantially faster than ssh, and is used when security is not a critical issue. A common example of this situation occurs when the cluster is behind a firewall and rsh is enabled just within the cluster. Setting up ssh is described in Chapter 5, and a book on ssh has recently appeared [11].

Here is a simple example. Suppose that we have a file called 'hosts' with the names of all the hosts in our cluster. We want to run a command (in parallel) on all those hosts. We can do so with a simple shell script as follows:

     #! /bin/bash
     for i in 'cat hosts' ;
         do (ssh -x $i hostname & ) ;
     done

If everything is working correctly and ssh has been configured so that it does not require a password on every invocation, then we should get back the names of the hosts in our cluster, although not necessarily in the same order as they appear in the file.

(What is that -x doing there? In this example, since the remotely executed program (hostname) does not use any X windowing facilities, we turn off X forwarding by using the -x option. To run a program that does use X, the X option must be turned on by the sshd server at each remote machine and the user should set the DISPLAY environment variable. Then, the connection to the X display is automatically forwarded in such a way that any X programs started from the shell will go through the encrypted channel, and the connection to the real X server will be made from the local machine. We note that if you run several X programs at several different hosts, they will each create a file named '.Xauthority' in your home directory on each of the machines. If the machines all have the same home directory, for example mounted via NFS, the '.Xauthority' files will conflict with each other.)

Other Process Managers

Programs such as the ones rsh and ssh contact to fork processes on their behalf are often called daemons. These processes are started when the system is booted and run forever, waiting for connections. You can see whether the ssh daemon is installed and running on a particular host by logging into that host and doing ps auxw | grep sshd. Other daemons, either run as root by the system or run by a particular user, can be used to start processes. Two examples are the daemons used to start processes in resource managers and the mpd's that can be used to start MPI jobs quickly (see Chapter 8).

7.2.4 Files

Having discussed how processes are started, we next tunr to the topic of remote files, files that are local to a remote machine. Often we need to move files from one host to another, to prepare for remote execution, to communicate results, or even to notify remote processes of events.

Moving files is not always necessary, of course. On some clusters, certain file systems are accessible on all the hosts through a system like NFS (Network File System) or PVFS (Parallel Virtual File System). ( Chapter 19 describes PVFS in detail.) However, direct remote access can sometimes be slower than local access. In this section we discuss some mechanisms for moving files from one host to another, on the assumption that the programs and at least some of the files they use are desired to be staged to a local file system on each host, such as '/tmp'.

rcp

The simplest mechanism is the remote copy command rcp. It has the same syntax as the standard local file copy command cp but can accept user name and host information from the file name arguments. For example,

     rcp thisfile jeeves.uw.edu:/home/jones/thatfile

copies a local file to a specific location on the host specified by the prefix before the ':'. A remote user can also be added:

     rcp smith@jeeves.uw.edu:/home/jones/thatfile .

The rcp command uses the same authentication mechanism as rsh does, so it will either ask for a password or not depending on how rsh has been set up. Indeed, rcp can be thought of as a companion program to rsh. The rcp command can handle "third party" transfers, in which neither the source nor destination file is on the local machine.

scp

Just as ssh is replacing rsh for security reasons, scp is replacing rcp. The scp command is the ssh version of rcp and has a number of other convenient features, such as a progress indicator, which is handy when large files are being transferred.

The syntax of scp is similar to that for rcp. For example,

     scp jones@fronk.cs.jx.edu:bazz .

will log in to machine fronk.cs.jx.edu as user jones (prompting for a password for jones if necessary) and then copy the file 'bazz' in user jones's home directory to the file 'bazz' in the current directory on the local machine.

ftp and sftp

Both ftp and sftp are interactive programs, usually used to browse directories and transfer files from "very" remote hosts rather than within a cluster. If you are not already familiar with ftp, the man page will teach you how to work this basic program. The sftp program is the more secure, ssh-based version of ftp.

rdist

One can use rdist to maintain identical copies of a set of files across a set of hosts. A flexible 'distfile' controls exactly what files are updated. This is a useful utility when one wants to update a master copy and then have the changes reflected in local copies on other hosts in a cluster. Either rsh-style (the default) or ssh-style security can be specified.

rsync

An efficient replacement for rcp is rsync, particularly when an earlier version of a file or directory to be copied already exists on the remote machine. The idea is to detect the differences between the files and then just transfer the differences over the network. This is especially effective for backing up large directory trees; the whole directory is specified in the command, but only (portions of) the changed files are actually copied.

7.2.5 Interprocess Communication with Sockets

The most common and flexible way for two processes on different hosts in a cluster to communicate is through sockets. A socket between two processes is a bidirectional channel that is accessed by the processes using the same read and write functions that processes use for file I/O. In this section we show how a process connects to another process, establishing a socket, and then uses it for communication. An excellent reference for the deep topic of sockets and TCP/IP in general is [111]. Here we just scratch the surface, but the examples we present here should enable you to write some useful programs using sockets. Since sockets are typically accessed from programming and scripting languages, we give examples in C, Perl, and Python, all of which are common languages for programming clusters.

Although once a socket is established, it is symmetric in the sense that communication is bidirectional, the initial setup process is asymmetric: one process connects; the other one "listens" for a connection and then accepts it. Because this situation occurs in many client/server applications, we call the process that waits for a connection the server and the process that connects to it the client, even though they may play different roles after the socket has been established.

We present essentially the same example in three languages. In the example, the server runs forever in the background, waiting for a socket connection. It advertises its location by announcing its host and "port" (more on ports below), on which it can be contacted. Then any client program that knows the host and port can set up a connection with the server. In our simple example, when the server gets the connection request, it accepts the request, reads and processes the message that the client sends it, and then sends a reply.

Client and Server in C

The server is shown in Figure 7.2. Let us walk through this example, which may appear more complex than it really is. Most of the complexity surrounds the sockaddr_in data structure, which is used for two-way communication with the kernel.

Start Figure 
 #include <stdio.h>
 #include <sys/types.h>
 #include <sys/socket.h>
 #include <netinet/in.h>
 
 main(int argc,char *argv[])
 {
     int rc, n, len, listen_socket, talk_socket;
     char buf[1024];
     struct sockaddr_in sin, from;
 
     listen_socket = socket(AF_INET, SOCK_STREAM, 0);
 
     bzero(&sin, sizeof(sin));
     sin.sin_family = AF_INET;
     sin.sin_addr.s_addr = INADDR_ANY;
     sin.sin_port = htons(0);
 
     bind(listen_socket, (struct sockaddr *) &sin ,sizeof(sin));
     listen(listen_socket, 5);
 
     getsockname(listen_socket, (struct sockaddr *) &sin, &len);
     printf("listening on port = %d\n", ntohs(sin.sin_port));
 
     while (1) {
         talk_socket = accept(listen_socket,
                              (struct sockaddr *) &from, &len);
         n = read(talk_socket, buf, 1024);
         write(talk_socket, buf, n);    /* echo */
         close(talk_socket);
     }
 }
End Figure

Figure 7.2: A simple server in C

First, we acquire a socket with the socket system call. Note that we use the word "socket" both for the connection between the two processes, as we have used it up to now, and for a single "end" of the socket as it appears inside a program, as here. Here a socket is a small integer, a file descriptor just like the ones used to represent open files. Our call creates an Internet (AF_INET) stream (SOCK_STREAM) socket, which is how one specifies a TCP socket. (The third argument is relevant only to "raw" sockets, which we are not interested in here. It is usually set to zero.) This is our "listening socket," on which we will receive connection requests. We then initialize the sockaddr_in data structure, setting its field sin_port to 0 to indicate that we want the system to select a port for us. A port is an operating system resource that can be made visible to other hosts on the network. We bind our listening socket to this port with the bind system call and notify the kernel that we wish it to accept incoming connections from clients on this port with the listen call. (The second argument to listen is the number of queued connection requests we want the kernel to maintain for us. In most Unix systems this will be 5.) At this point clients can connect to this port but not yet to our actual server process. Also, at this point no one knows what port we have been assigned.

We now publish the address of the port on which we can be contacted. Many standard daemons listen on "well known" ports, but we have not asked for a specific port, so our listening socket has been assigned a port number that no one yet knows. We ourselves find out what it is with the getsockname system call and, in this case, just print it on stdout.

At this point we enter an infinite loop, waiting for connections. The accept system call blocks until there is a connection request from a client. Then it returns a new socket on which we are connected to the client, so that it can continue listening on the original socket. Our server simply reads some data from the client on the new socket (talk_socket), echoes it back to the client, closes the new socket, and goes back to listening for another connection.

This example is extremely simple. We have not checked for failures of any kind (by checking the return codes from our system calls), and of course our server does not provide much service. However, this example does illustrate how to code a common sequence of system calls (the socket-bind-listen sequence) that is used in nearly all socket setup code.

The corresponding client is shown in Figure 7.3. In order to connect to the server, it must know the name of the host where the server is running and the number of the port on which it is listening. We supply these here as command-line arguments.

Start Figure 
 #include <stdio.h>
 #include <sys/types.h>
 #include <sys/socket.h>
 #include <netdb.h>
 #include <netinet/in.h>
 
 main(int argc,char *argv[])
 {
     int rc, n, talk_socket;
     char buf[1024] = "test msg";
     struct sockaddr_in sin;
     struct hostent *hp;
 
     talk_socket = socket(AF_INET, SOCK_STREAM, 0);
 
     hp = gethostbyname(argv[1]);
     bzero((void *)&sin, sizeof(sin));
     bcopy((void *) hp->h_addr, (void *) &sin.sin_addr, hp->h_length);
     sin.sin_family = hp->h_addrtype;
     sin.sin_port = htons(atoi(argv[2]));
 
     connect(talk_socket,(struct sockaddr *) &sin, sizeof(sin));
 
     n = write(talk_socket, buf, strlen(buf)+1);
     buf[0] = '\0';    /* empty the buffer */
     n = read(talk_socket, buf, 1024);
     printf("received from server: %s \n",buf);
 }
End Figure

Figure 7.3: A simple client in C

Again we acquire a socket with the socket system call. We then fill in the sockaddr_in structure with the host and port (first calling gethostbyname to fill in the hostent structure needed to be placed in sin). Next we call connect to create the socket. When connect returns, the accept has taken place in the server, and we can write to and read from the socket as a way of communicating with the server. Here we send a message and read a response, which we print.

Client and Server in Python

Python is an object-oriented scripting language. Implementations exist for Unix and Windows; see www.python.org for details. It provides an extensive set of modules for interfacing with the operating system. One interesting feature of Python is that the block structure of the code is given by the indentation of the code, rather than explicit "begin"/ "end" or enclosing braces.

Much of the complexity of dealing with sockets has to do with properly managing the sockaddr data structure. Higher-level languages like Python and Perl make socket programming more convenient by hiding this data structure. A number of good books on Python exist that include details of the socket module; see, for example, [14] and [70]. Python uses an exception handling model (not illustrated here) for error conditions, leading to very clean code that does not ignore errors. The Python version of the server code is shown in Figure 7.4. Here we use the "well-known port" approach: rather than ask for a port, we specify the one we want to use. One can see the same socket-bind-listen sequence as in the C example, where now a socket object (s) is returned by the socket call and bind, listen, and accept are methods belonging to the socket object. The accept method returns two objects, a socket (conn) and information (addr) on the host and port on the other (connecting) end of the socket. The methods send and recv are methods on the socket object conn, and so this server accomplishes the same thing as the one in Figure 7.2.

Start Figure 
 #! /usr/bin/env python
 #echo server program
 from socket import *
 HOST = ''                    # symbolic name for local host
 PORT = 50007                 # arbibrary port
 s = socket(AF_INET, SOCK_STREAM)
 s.bind((HOST, PORT))
 s.listen(1)
 conn, addr = s.accept()
 print 'connected to by', addr
 while 1:
   data = conn.recv(1024)
   if not data:
     break
   conn.send(data)
 conn.close()
End Figure

Figure 7.4: A simple server in Python

The Python code for the corresponding client is shown in Figure 7.5. It has simply hard-coded the well-known location of the server.

Start Figure 
 #!/usr/bin/env python
 # Echo client program
 from socket import *
 HOST = 'donner.mcs.anl.gov'     # the remote host
 PORT = 50007
 s = socket(AF_INET, SOCK_STREAM)
 s.connect((HOST, PORT))
 s.send('Hello, world')
 data = s.recv(1024)
 s.close()
 print 'Received', 'data'
End Figure

Figure 7.5: A simple client in Python

Client and Server in Perl

Perl [124] is a powerful and popular scripting language. Versions exist for Unix and for Windows; see www.perl.com for more information. Perl provides a powerful set of string matching and manipulation operations, combined with access to many of the fundamental system calls. The man page perlipc has samples of clients and servers that use sockets for communication.

The code for a "time server" in Perl is shown in Figure 7.6. It follows the same pattern as our other servers. The code for the corresponding client is shown in Figure 7.7.

Start Figure 
 #!/usr/bin/perl
 
 use strict;
 use Socket;
 use FileHandle;
 
 my $port  = shift || 12345;
 my $proto = getprotobyname('tcp');
 socket(SOCK, PF_INET, SOCK_STREAM, $proto)
     || die "socket: $!";
 SOCK->autoflush();
 setsockopt(SOCK, SOL_SOCKET, SO_REUSEADDR, pack("1", 1))
     || die "setsockopt: $! ";
 bind(SOCK, sockaddr_in($port, INADDR_ANY))
     || die "bind: $!";
 listen(SOCK,SOMAXCONN)
     || die "listen: $!";
 
 print "server started on port $port\n";
 
 while (1)
 {
     my $paddr = accept(CLIENT,SOCK);
     CLIENT->autoflush();
     my $msg = <CLIENT>;
     print "server: recvd from client: $msg \n";
     print CLIENT "Hello there, it's now ", scalar localtime, "\n";
     close(CLIENT);
 }
End Figure

Figure 7.6: A simple server in Perl
Start Figure 
 #!/usr/bin/perl -w
 
 use strict;
 use Socket;
 use FileHandle;
 
 my ($host,$port, $iaddr, $paddr, $proto, $line);
 
 $host = shift || 'localhost';
 $port = shift || 12345;
 
 $iaddr = inet_aton($host)
     || die "no valid host specified: $host";
 $paddr = sockaddr_in($port, $iaddr);  # packed addr
 
 $proto = getprotobyname('tcp');
 socket(SOCK, PF_INET, SOCK_STREAM, $proto)
     || die "socket failed: $!";
 SOCK->autoflush();  # from FileHandle
 connect(SOCK, $paddr)
     || die "connect failed: $!";
 print SOCK "hello from client\n";
 $line = <SOCK>;
 print "client: recvd from server: $line \n";
End Figure

Figure 7.7: A simple client in Perl

7.2.6 Managing Multiple Sockets with Select

So far our example socket code has involved only one socket open by the server at a time (not counting the listening socket). Further, the connections have been short lived: after accepting a connection request, the server handled that request and then terminated the connection. This is a typical pattern for a classical server but may not be efficient for manager/worker algorithms in which we might want to keep the connections to the workers open rather than reestablish them each time. Unlike the clients in the examples above, the workers are persistent, so it makes sense to make their connections persistent as well.

What is needed by the manager in this case is a mechanism to wait for communication from any of a set of workers simultaneously. Unix provides this capability with the select system call. The use of select allows a process to block, waiting for a change of state on any of a set of sockets. It then "wakes up" the process and presents it with a list of sockets on which there is activity, such as a connection request or a message to be read. We will not cover all of the many aspects of select here, but the code in Figure 7.8 illustrates the features most needed for manager/worker algorithms. For compactness, we show this in Python. A C version would have the same logic. See the select man page or [111] for the details of how to use select in C. It is also available, of course, in Perl.

Start Figure 
 #!/usr/bin/env python
 
 from socket import socket, AF_INET, SOCK_STREAM
 from select import select
 
 lsock = socket(AF_INET,SOCK_STREAM)
 lsock.bind(('',0)) # this host, anonymous port
 lsock.listen(5)
 lport = lsock.getsockname()[1]
 print 'listening on port =', lport
 
 sockets = [lsock]
 while 1:
     (inReadySockets, None, None) = select(sockets, [], [])
     for sock in inReadySockets:
         if sock == lsock:
             (tsock,taddr) = lsock.accept()
             sockets.append(tsock)
         else:
             msg = sock.recv(1024)
             if msg:
                 print 'recvd msg=', msg
             else:
                 sockets.remove(sock)
                 sock.close()
End Figure

Figure 7.8: A Python server that uses select

The first part of the code in Figure 7.8 is familiar. We acquire a socket, bind it to a port, and listen on it. Then, instead of doing an accept on this socket directly, we put it into a list (sockets). Initially it is the only member of this list, but eventually the list will grow. Then we call select. The arguments to select are three lists of sockets we are interested in for reading, writing, or other events. The select call blocks until activity occurs on one of the sockets we have given to it. When select returns, it returns three lists, each a sublist of the corresponding input lists. Each of the returned sockets has changed state, and one can take some action on it with the knowledge that the action will not block.

In our case, we loop through the returned sockets, which are now active. We process activity on the listening socket by accepting the connection request and then adding the new connection to the list of sockets we are interested in. Otherwise we read and print the message that the client has sent us. If our read attempt yields an empty message, we interpret this as meaning that the worker has closed its end of the socket (or exited, which will close the socket), and we remove this socket from the list.

We can test this server with the client in Figure 7.9.

Start Figure 
 #!/usr/bin/env python
 
 from sys    import argv, stdin
 from socket import socket, AF_INET, SOCK_STREAM
 
 sock = socket(AF_INET,SOCK_STREAM)
 sock.connect((argv[1],int(argv[2])))
 
 print 'sock=', sock
 while 1:
    print 'enter something:'
    msg = stdin.readline()
    if msg:
        sock.sendall(msg.strip())  # strip nl
    else:
        break

7.3 Parameter Studies

One straightforward application of task parallelism is the "parameter study", in which the same sequential program is run multiple times with different sets of input parameters. Since the program to be run is sequential, there is no communication among the workers, and the manager can be a simple script that communicates with the workers by means of the arguments to the sequential program and its standard output. We can start the workers with ssh and collect the output by using the popen system call, which returns a file descriptor we can select on and read the remote process's stdout from.

Although both the algorithm we use and its implementation are general, we present here a concrete example. We explore the parameter space of compiler options for the default Linux C compiler gcc. The man page for gcc conveniently lists in one place all the options that can be passed to gcc to cause it to produce faster machine code. Here is an excerpt from the man page:

     Optimization Options
         -fcaller-saves -fcse-follow-jumps -fcse-skip-blocks
         -fdelayed-branch -felide-constructors
         -fexpensive-optimizations -ffast-math -ffloat-store
         -fforce-addr -fforce-mem -finline-functions
         -fkeep-inline-functions -fmemoize-lookups
         -fno-default-inline -fno-defer-pop
         -fno-function-cse -fno-inline -fno-peephole
         -fomit-frame-pointer -frerun-cse-after-loop
         -fschedule-insns -fschedule-insns2
         -fstrength-reduce -fthread-jumps -funroll-all-loops
         -funroll-loops -0 -02 -03

For the matrix-matrix multiply program we are going to test with, which has no function calls, only some of these look useful. Here is a subset of the above list containing optimization flags that might have an effect on the speed of the program:

     -fexpensive-optimizations
     -ffast-math
     -ffloat-store
     -fno-peephole
     -fschedule-insns
     -fschedule-insns2
     -fstrength-reduce
     -funroll-all-loops
     -funroll-loops
     -0
     -02
     -03

Since there are twelve switches that can be either present or absent, there are 212 possible combinations. These are not completely independent, since some switch settings imply others, especially the three -0 flags, but we will ignore thus fact for the sake of simplifying our example, and just try all 4096 combinations, Indeed, which switch settings are redundant in the presence of others should be deducible from our results!

Our plan will be to take a simple test program and compile it with all possible switch combinations and run it, reporting back the times. Since we have 4096 jobs to run, the use of a cluster will make a big difference, even if the individual tasks are short.

For our test program, we will use a straightforward matrix-matrix multiply program, shown in Figure 7.10. It multiples two 300 ?300 matrices, timing the calculation, this may not be the highest performing way to do this, but it will do for our purposes. The program echoes its command line arguments, which it does not otherwise use; we will use them to help us record the arguments used to compile the program.

Start Figure 
 #include <stdio.h>
 #include <sys/time.h>
 #include <unistd.h>
 #define SIZE 300
 
 main(int argc, char *argv[])
 {
     double a[SIZE][SIZE], b[SIZE][SIZE], c[SIZE][SIZE];
     int i, j, k;
     struct timeval tv;
     double starttime, endtime;
 
     for (i = 0; i < SIZE; i++)
         for (j = 0; j < SIZE; j++)
             a[i][j] = (double) (i + j);
     for (i = 0; i < SIZE; i++)
         for (j = 0; j < SIZE; j++)
             b[i][j] = (double) (i + j);
     for (i = 0; i < SIZE; i++)
         for (j = 0; j < SIZE; j++)
             c[i][j] = 0.0;
 
     gettimeofday( &tv, ( struct timezone * ) 0 );
     starttime = tv.tv_sec + (tv.tv_usec / 1000000.0);
     for (i = 0; i < SIZE; i++) {
         for (j = 0; j < SIZE; j++) {
             for (k = 0; k < SIZE; k++) {
                 c[i][j] = c[i][j] + a[i][k] * b [k][j];
             }
         }
     }
     gettimeofday( &tv, ( struct timezone * ) 0 );
     endtime = tv.tv_sec + (tv.tv_usec / 1000000.0);
     printf("%f seconds for", endtime - starttime);
     for (i = 1; i < argc; i++)
         printf(" %s", argv[i]);
     printf("\n");
 }
End Figure

Figure 7.10: Matrix-matrix multiply program

Our worker programs will just be the sequence

     gcc <flags> -o matmult matmult.c
     matmult

and the manager will start them with ssh, on hosts whose names are in a file. The other argument to our manager is a file of possible arguments. It contains exactly the twelve lines listed above. The manager just steps through the numbers from 0 up to the total number of runs (in our case 4096) treating each number as a binary number where a 1 bit represent the presence of the compiler switch corresponding to that position in the binary number. Thus we will run through all possible combinations.

The overall plan is to loop through the parameter space represented by the binary numbers represented by the binary numbers from 0 to 212. If there is a free host (no worker is working there) we assign it the next task; if not we select on the sockets that are open to currently working workers. When one of them reports back, we add it back to the list of free hosts. At the end, after all the work has been assigned, we still have to wait for the last tasks to complete.

Let us step through the code in Figure 7.11 in detail. First we read in the list of hosts (initial value of the list freeHosts) and the list of possible arguments (parmList). We initialize the set of sockets to select on to empty since there are no workers yet, and create an empty Python dictionary (fd2host) where we will keep track of busy hosts and the connections to them. We set numParmSets to the number of subtasks, which we can calculate from the number of possible compiler flags in the input file. Then we enter the main loop, which runs until we have assigned all the work and there are no outstanding workers working. If there is a subtask still to do and a free host to do it on, we construct the parameter list corresponding to the next task (in ParmSet), and pick the first host from the list of free hosts, temporarily removing it from the list. We then build a string containing the specification of the subtask. The Popen3 command forks a process that runs the ssh program locally, which runs the gcc-matmult sequence remotely. The ssh's, and therefore the remote processes, run in parallel.

Start Figure 
 #!/usr/bin/python
 
 from sys    import argv
 from popen2 import Popen3
 from select import select, error
 
 hostFile = open(argv[1])
 parmsFile = open(argv[2])
 freeHosts = [ line.strip() for line in hostFile.readlines() ]
 parmList = [ line.strip() for line in parmsFile.readlines() ]
 lenParmList = len(parmList)
 socketsToSelect = []
 fd2host = {}
 numParmSets = 2 ** lenParmList
 pcnt = 0
 while pcnt < numParmSets  or  socketsToSelect:
     if pcnt < numParmSets  and  freeHosts:
         parmSet = []
         for i in range(0,lenParmList):
             bit = 1 << i
             if bit & pcnt:
                 parmSet.append(parmList[lenParmList-i-1])
         host = freeHosts[0]
         freeHosts.remove(host)
         cmd = ("ssh -l lusk -x -n %s 'gcc %s -o matmult matmult.c; " +
                "matmult %s'") % (host,' '.join(parmSet),' '.join(parmSet))
         runner = Popen3(cmd)
         runfd = runner.fromchild
         socketsToSelect.append(runfd)
         fd2host[runfd] = host
         pcnt += 1
     else:
         readyFDs = 0
         (readyFDs,None,None) = select(socketsToSelect,[],[],30)
         for fd in readyFDs:
             line = fd.readline()
             if line:
                 print '%s on %s' % (line.strip(),fd2host[fd])
             else:
                 freeHosts.append(fd2host[fd])
                 socketsToSelect.remove(fd)
                 fd.close()
End Figure

Figure 7.11: Manager for parameter study

We set runfd to the stdout of the ssh, which collects the stdout from the matmult. Each line of stdout will contain the time followed by the compiler flags used. Then we add this fd to the list of sockets available for selecting on and enter into the list fd2host the host attached to that fd.

If there are no free hosts or we have already assigned all the subtasks, then we select on the sockets connected to busy workers. When one those sockets becomes active, it means that the associated worker has set us a line of output. We read it and print it, or if the read fails (the worker exited, which sends an EOF on the socket), we close that socket, take it out of the list of sockets to select on, and add the corresponding host to the list of free hosts, since it can mow be assigned another subtask.

The manager exits once all the subtasks have been done and all the workers have completed. If we run this with

     parmstudy.py hostfile parmfile | sort -n

then we will get the best combinations at the top of the list. Try it!

7.5 Decomposing Programs Into Communicating Processes

Not all problems can be divided into independent tasks. As we saw in Section 1.3.6, some applications are too large, in terms of their memory or compute needs, for a single processor or even a single SMP node. Solving these problems requires breaking the task into communicating (rather than independent) processes. In this section we will introduce two examples of decomposing a single task into multiple communicating processes. Because these programs are usually written using a message-passing programming model such as MPI or PVM, the details of implementing these examples are left to the chapters on these programming models.

7.5.1 Domain Decomposition

Many problems, such as the 3-dimensional partial differential equation (PDE) introduced in Section 1.3.6, are described by an approximation on a mesh of values. This mesh can be structured (also called regular) or unstructured. These meshes can be very large (as in the example in Chapter 1) and require more memory and computer power than a single processor or node can supply. Fortunately, the

For simplicity, we consider a two-dimensional example. A simple PDE is the Poisson equation,

∇2u

=

f in the interior,

u

=

0 on the boundary

where f is a given function and the problem is to find u. To further simplify the problem, we have chosen Dirichlet boundary conditions, which just means that the value of u along the boundary is zero. Finally, the domain is the unit square [0, 1] ?[0, 1]. A very simple discretization of this problem uses a finite difference approximation to the derivatives, yielding the approximation

Click To expand

Defining a mesh of points (xi, yj) = (i ?h, j ?h) with h = 1/n, and using the ui,j to represent the approximation of u(xi, yj), we get

(7.1)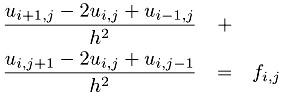

We can now represent this using two dimensional arrays. We'll use Fortran because Fortran has some features that will make these examples easier to write. We will use U(i, j) as our computed value for ui,j.

To solve this approximation for the Poisson problem, we need to find the the values of U. This is harder than it may seem at first, because Equation 7.1 must be satisified at all points on the mesh (i.e., all values of i and j) simultaneously. In fact, this equation leads to a system of simultaneous linear equations. Excellent software exists to solve this problem (see Chapter 12), but we will use a very simple approach to illustrate how this problem can be parallelized. The first step is to write this problem as an iterative process

Click To expand

This is the Jacobi iteration, and can be written in Fortran as

    real UNEW(0:n,0:n), U(0:n,0:n), F(1:n-1,1:n-1)
    ... code to initialize U and F
    do iter=1,itermax
        do j=1,n-1
            do i=1,n-1
                UNEW(i,j) = 0.25 * (U(i+1,j)+U(i-1,j) +     &
                                    U(i,j+1)+U(i,j-1) - F(i,j))
            enddo
        enddo
        ... code to determine if the iteration has converged
    enddo

At this point, we can see how to divide this problem across multiple processors. The simplest approach is to divide the mesh into small pieces, giving each piece to a separate processor. For example, we could divide the original mesh (U(0:n,0:n) in the code) into two parts: U(0:n,0:n/2) and (U(0:n,n/2+1:n). This approach is called domain decomposition, and is based on using the decompositions of the physical domain (the unit square in this case) to create parallelism.

Applying this approach for two processors, we have the two code fragments shown in Figure 7.12. Note that each process now has only half of the data because each array is declared with only the data "owned" by that processor. This also shows why we used Fortran; the ability to specify the range of the indices for the arrays in Fortran makes these codes very easy to write.

Start Figure

Code for process zero

    real UNEW(0:n,0:n/2), U(0:n,0:n/2), F(1:n-1,1:n/2)
    ... code to initialize u and f
    do iter=1,itermax
        do j=1,n/2
            do i=1,n-1
                UNEW(i,j) = 0.25 * (U(i+1,j)+U(i-1,j) +     &
                                    U(i,j+1)+U(i,j-1) - F(i,j))
            enddo
        enddo
        ... code to determine if the iteration has converged
    enddo

Code for process one

    real UNEW(0:n,n/2+1:n), U(0:n,n/2+1:n), F(1:n-1,n/2+1:n-1)
    ... code to initialize u and f
    do iter=1,itermax
        do j=n/2+1,n-1
            do i=1,n-1
                UNEW(i,j) = 0.25 * (U(i+1,j)+U(i-1,j) +     &
                                    U(i,j+1)+U(i,j-1) - F(i,j))
            enddo
        enddo
        ... code to determine if the iteration has converged
    enddo
End Figure

Figure 7.12: Two code fragments for parallelizing the Poisson problem with the Jacobi iteration

However, unlike the decompositions into independent tasks in the first part of this chapter, this decomposition does not produce indepentent tasks. Consider the case of j=n/2 in the original code. Process zero in Figure 7.12 computes the values of UNEW(i,n/2). However, to do this, it needs the values of U(i,n/2+1). This data is owned by processor one. In order to make this code work, we must communicate the data owned by processor one (the values of U(i,n/2+1) for i=1,...,n-1) to processor zero. We must also allocate another row of storage to hold these values; this extra row is often called a ghost points or a halo. The resulting code is shown in Figure 7.13.

Start Figure

Code for process zero

    real UNEW(0:n,0:n/2+1), U(0:n,0:n/2+1), F(1:n-1,1:n/2)
    ... code to initialize u and f
    do iter=1,itermax
        ... code to Get u(i,n/2+1) from process one
        do j=1,n/2
            do i=1,n-1
                UNEW(i,j) = 0.25 * (U(i+1,j)+U(i-1,j) +     &
                                    U(i,j+1)+U(i,j-1) - F(i,j))
            enddo
        enddo
        ... code to determine if the iteration has converged
    enddo

Code for process one

    real UNEW(0:n,n/2:n), U(0:n,n/2:n), F(1:n-1,n/2+1:n-1)
    ... code to initialize u and f
    do iter=1,itermax
        ... code to Get u(i,n/2) from process zero
        do j=n/2+1,n-1
            do i=1,n-1
                UNEW(i,j) = 0.25 * (U(i+1,j)+U(i-1,j) +     &
                                    U(i,j+1)+U(i,j-1) - F(i,j))
            enddo
        enddo
        ... code to determine if the iteration has converged
    enddo
End Figure

Figure 7.13: Two code fragments for parallelizing the Poisson problem with the Jacobi iteration, including the communication of ghost points. Note the changes in the declarations for U and UNEW.

Note also that although both processes have variables named UNEW and i, these are different variables. This kind of parallel programming model is sometimes called a shared-nothing model because no data (variables or instructions) are shared between the processes. Instead, explicit communication is required to move data from one process to another. Section 8.3 discusses this example in detail, using the Message Passing Interface (MPI) to implement the communication of data between the processors, using code written in C.

There are more complex and powerful domain decomposition techniques, but they all start from dividing the domain (usually the physical domain of the problem) into a number of separate pieces. These pieces must communicate along their edges at each step of the computation. As described in Section 1.3.6, a decomposition into squares (in two-dimensions) or cubes (in three dimensions) reduces the amount of data that must be communicated because those shapes maximize the volume to surface area ratio for rectangular solids.

7.5.2 Data Structure Decomposition

Not all problems have an obvious decomposition in terms of a physical domain. For these problems, a related approach that decomposes the data-structures in the application can be applied. An example of this kind of application is the solution of a system of linear equations Ax = b, where the equations are said to be dense. This simply means that most of the elements of the matrix describing the problem are non-zero. A good algorihm for solving this problem is called LU factorization, because it involves first computing a lower trianular matrix L and an upper triangular matrix U such that the original matrix A is given by the product LU. Because an lower (resp. upper) triangular matrix has only zero elements below (resp. above) the diagonal, it is easy to find the solution x once L and U are known. This is the algorithm used in the LINPACK [34] benchmark. A parallel verison of this is used in the High-Performance Linpack benchmark, and this section will sketch out some of the steps used in parallelizing this kind of problem.

The LU factorization algorithm looks something like the code shown in Figure 7.14, an n ?n matrix A represented by the Fortran array a(n,n).

Start Figure 
 real a(n,n)
 do i=i, n
    do k=1,i-1
        sum = 0
        do j=1,k-1
            sum = sum + a(i,j)*a(j,k)
        enddo
        a(i,k) = (a(i,k) - sum) / a(k,k)
    enddo
    do k=1,i
        sum = 0
        do j=1,k-1
            sum = sum + a(k,j)*a(j,i)
        enddo
        a(k,i) = a(k,i) - sum
    enddo
 enddo
End Figure

Figure 7.14: LU Factorization code. The factors L and U are computed in-place; that is, they are stored over the input matrix a.

An obvious way to decompose this problem, following the domain decomposition discussion, is to divide the matrix into groups of rows (or groups of columns):

However, this will yield an inefficient program. Because of the outer-loop over the rows of the matrix (the loop over i), once i reaches n/4 in the case of four processors, processor zero has no work left to do. As the computation proceeds, fewer and fewer processors can help with the computation. For this reason, more complex decompositions are used. For example, the ScaLAPACK library uses the two-dimensional block-cyclic distribution shown here:

This decomposition ensures that most processors are in use until the very end of the algorithm.

Just as in the domain decomposition example, communication is required to move data from one processor to another. In this example, data from the ith row must be communicated from the processors that hold that data to the processors holding the data needed for the computations (the loops over j). We do not show the communication here; see the literature on solving dense linear systems in parallel for details on these algorithms.

The technique of dividing the data structure among processors is a general one. Chosing the decomposition to use requires balancing the issues of load balance, communication, and algorithm complexity. Addressing these may suggest algorithmic modifications to provide better parallel performance. For example, certain variations of the LU factorization method described above may perform the floating-point operations in a different order. Because floating-point arithmetic is not associative, small differences in the results may occur. Other variations may produce answers that are equally valid as approximations but give results that are slightly different. Care must be exercised here, however, because some approximations are better behaved than others. Before changing the algorithm, make sure that you understand the consequences of any change. Consult with a numerical analysist or read about stability and well-posedness in any textbook on numerical computing.

7.5.3 Other Approaches

There are many techniques for creating parallel algorithms. Most involve dividing the problem into separate tasks that may need to communicate. For an effective decomposition for a Beowulf cluster, the amount of computation must be large relative to the amount of communication. Examples of these kinds of problems include sophisticated search and planning algorithms, where the results of some tests are used to speed up other tests (for example, a computation may discover that a subproblem has already been solved.).

Some computations are implemented as master/worker applications, where each worker is itself a parallel program (e.g., because of the memory needs or the requirement that the computation finish within a certain amount of time, such as overnight). Master/worker algorithms can also be made more sophisticated, guiding the choice and order of worker tasks by previous results returned by the workers.

Chapter 8: Parallel Programming with MPI

Overview

William Gropp and Ewing Lusk

Chapter 7 described how parallel computation on a Beowulf is accomplished by dividing a computation into parts, making use of multiple processes and executing each on a separate processor. Sometimes an ordinary program can be used by all the processes, but with distinct input files or parameters. In such a situation, no communication occurs among the separate tasks. When the power of a parallel computer is needed to attack a large problem with a more complex structure, however, such communication is necessary.

One of the most straightforward approaches to communication is to have the processes coordinate their activities by sending and receiving messages, much as a group of people might cooperate to perform a complex task. This approach to achieving parallelism is called message passing.

In this chapter and the next, we show how to write parallel programs using MPI, the Message Passing Interface. MPI is a message-passing library specification. All three parts of the following description are significant.

  • MPI addresses the message-passing model of parallel computation, in which processes with separate address spaces synchronize with one another and move data from the address space of one process to that of another by sending and receiving messages. [ 1]

  • MPI specifies a library interface, that is, a collection of subroutines and their arguments. It is not a language; rather, MPI routines are called from programs written in conventional languages such as Fortran, C, and C++.

  • MPI is a specification, not a particular implementation. The specification was created by the MPI Forum, a group of parallel computer vendors, computer scientists, and users who came together to cooperatively work out a community standard. The first phase of meetings resulted in a release of the standard in 1994 that is sometimes referred to as MPI-1. Once the standard was implemented and in wide use a second series of meetings resulted in a set of extensions, referred to as MPI-2. MPI refers to both MPI-1 and MPI-2.

As a specification, MPI is defined by a standards document, the way C, Fortran, or POSIX are defined. The MPI standards documents are available at www.mpi-forum.org and may be freely downloaded. The MPI-1 and MPI-2 standards are available as journal issues [ 72, 73] and in annotated form as books in this series [ 105, 46]. Implementations of MPI are available for almost all parallel computers, from clusters to the largest and most powerful parallel computers in the world. In Section 8.9 we summarizes the most popular cluster implementations.

A goal of the MPI Forum was to create a powerful, flexible library that could be implemented efficiently on the largest computers and provide a tool to attack the most difficult problems in parallel computing. It does not always do the simplest tasks in the simplest way but comes into its own as more complex functionality is needed. As a result, many tools and libraries have been built on top of MPI (see Table 9.1 and Chapter 12). To get the flavor of MPI programming, in this chapter and the next we work through a set of examples, starting with the simplest.

[1]Processes may be single threaded, with one program counter, or multithreaded, with multiple program counters. MPI is for communication among processes rather than threads. Signal handlers can be thought of as executing in a separate thread.

8.1 Hello World in MPI

To see what an MPI program looks like, we start with the classic "hello world" program. MPI specifies only the library calls to be used in a C, Fortran, or C++ program; consequently, all of the capabilities of the language are available. The simplest "Hello World" program is shown in Figure 8.1.

Start Figure 
 #include "mpi.h"
 #include <stdio.h>
 
 int main( int argc, char *argv[] )
 {
     MPI_Init( &argc, &argv );
     printf( "Hello World\n" );
     MPI_Finalize();
     return 0;
 }
End Figure

Figure 8.1: Simple "Hello World" program in MPI.

All MPI programs must contain one call to MPI_Init (or MPI_Init_thread, described in Section 9.9) and one to MPI_Finalize. All other[ 2] MPI routines must be called after MPI_Init and before MPI_Finalize. All C and C++ programs must also include the file 'mpi.h'; Fortran programs must either use the MPI module or include mpif.h.

The simple program in Figure 8.1 is not very interesting. In particular, all processes print the same text. A more interesting version has each process identify itself. This version, shown in Figure 8.2, illustrates several important points. Of particular note are the variables rank and size. Because MPI programs are made up of communicating processes, each process has its own set of variables. In this case, each process has its own address space containing its own variables rank and size (and argc, argv, etc.). The routine MPI_Comm_size returns the number of processes in the MPI job in the second argument. Each of the MPI processes is identified by a number, called the rank, ranging from zero to the value of size minus one. The routine MPI_Comm_rank returns in the second argument the rank of the process. The output of this program might look something like the following:

     Hello World from process 0 of 4
     Hello World from process 2 of 4
     Hello World from process 3 of 4
     Hello World from process 1 of 4
Start Figure 
 #include "mpi.h"
 #include <stdio.h>
 
 int main( int argc, char *argv[] )
 {
     int rank, size;
 
     MPI_Init( &argc, &argv );
     MPI_Comm_rank( MPI_COMM_WORLD, &rank );
     MPI_Comm_size( MPI_COMM_WORLD, &size );
     printf( "Hello World from process %d of %d\n", rank, size );
     MPI_Finalize();
     return 0;
 }
End Figure

Figure 8.2: A more interesting version of "Hello World".

Note that the output is not ordered from processes 0 to 3. MPI does not specify the behavior of other routines or language statements such as printf; in particular, it does not specify the order of output from print statements. However, there are tools, built using MPI, that can provide ordered output of messages.

8.1.1 Compiling and Running MPI Programs

The MPI standard does not specify how to compile and link programs (neither do C or Fortran). However, most MPI implementations provide tools to compile and link programs.

For example, one popular implementation, MPICH, provides scripts to ensure that the correct include directories are specified and that the correct libraries are linked. The script mpicc can be used just like cc to compile and link C programs. Similarly, the scripts mpif77, mpif 90, and mpicxx may be used to compile and link Fortran 77, Fortran, and C++ programs.

If you prefer not to use these scripts, you need only ensure that the correct paths and libraries are provided. The MPICH implementation provides the switch -show for mpicc that shows the command lines used with the C compiler and is an easy way to find the paths. Note that the name of the MPI library may be 'libmpich.a', 'libmpi.a', or something similar and that additional libraries, such as 'libsocket.a' or 'libgm.a', may be required. The include path may refer to a specific installation of MPI, such as '/usr/include/local/mpich2-1.0/include'.

Running an MPI program (in most implementations) also requires a special program, particularly when parallel programs are started by a batch system as described in Chapter 14. Many implementations provide a program mpirun that can be used to start MPI programs. For example, the command

     mpirun -np 4 helloworld

runs the program helloworld using four processes.

The name and command-line arguments of the program that starts MPI programs were not specified by the original MPI standard, just as the C standard does not specify how to start C programs. However, the MPI Forum did recommend, as part of the MPI-2 standard, an mpiexec command and standard command-line arguments to be used in starting MPI programs. A number of MPI implementations including the all-new version of MPICH, called MPICH2, now provide mpiexec. The name mpiexec was selected because no MPI implementation was using it (many are using mpirun, but with incompatible arguments). The syntax is almost the same as for the MPICH version of mpirun; instead of using -np to specify the number of processes, the switch -n is used:

     mpiexec -n 4 helloworld

The MPI standard defines additional switches for mpiexec; for more details, see Section 4.1, "Portable MPI Process Startup," in the MPI-2 standard. For greatest portability, we recommend that the mpiexec form be used; if your preferred implementation does not support mpiexec, point the maintainers to the MPI-2 standard.

Most MPI implementations will attempt to run each process on a different processor; most MPI implementations provide a way to select particular processors for each MPI process.

8.1.2 Adding Communication to Hello World

The code in Figure 8.2 does not guarantee that the output will be printed in any particular order. To force a particular order for the output, and to illustrate how data is communicated between processes, we add communication to the "Hello World" program. The revised program implements the following algorithm:

     Find the name of the processor that is running the process
     If the process has rank > 0, then
         send the name of the processor to the process with rank 0
     Else
         print the name of this processor
         for each rank,
             receive the name of the processor and print it
     Endif

This program is shown in Figure 8.3. The new MPI calls are to MPI_Send and MPI_Recv and to MPI_Get_processor_name. The latter is a convenient way to get the name of the processor on which a process is running. MPI_Send and MPI_Recv can be understood by stepping back and considering the two requirements that must be satisfied to communicate data between two processes:

  1. Describe the data to be sent or the location in which to receive the data

  2. Describe the destination (for a send) or the source (for a receive) of the data.

Start Figure 
 #include "mpi.h"
 #include <stdio.h>
 
 int main( int argc, char *argv[] )
 {
     int  numprocs, myrank, namelen, i;
     char processor_name[MPI_MAX_PROCESSOR_NAME];
     char greeting[MPI_MAX_PROCESSOR_NAME + 80];
     MPI_Status status;
 
     MPI_Init( &argc, &argv );
     MPI_Comm_size( MPI_COMM_WORLD, &numprocs );
     MPI_Comm_rank( MPI_COMM_WORLD, &myrank );
     MPI_Get_processor_name( processor_name, &namelen );
 
     sprintf( greeting, "Hello, world, from process %d of %d on %s",
              myrank, numprocs, processor_name );
 
     if ( myrank == 0 ) {
         printf( "%s\n", greeting );
         for ( i = 1; i < numprocs; i++ ) {
             MPI_Recv( greeting, sizeof( greeting ), MPI_CHAR,
                       i, 1, MPI_COMM_WORLD, &status );
             printf( "%s\n", greeting );
         }
     }
     else {
         MPI_Send( greeting, strlen( greeting ) + 1, MPI_CHAR,
                   0, 1, MPI_COMM_WORLD );
     }
 
     MPI_Finalize( );
     return 0;
 }
End Figure

Figure 8.3: A more complex "Hello World" program in MPI. Only process 0 writes to stdout; each process sends a message to process 0.

In addition, MPI provides a way to tag messages and to discover information about the size and source of the message. We will discuss each of these in turn.

Describing the Data Buffer

A data buffer typically is described by an address and a length, such as "a,100," where a is a pointer to 100 bytes of data. For example, the Unix write call describes the data to be written with an address and length (along with a file descriptor). MPI generalizes this to provide two additional capabilities: describing noncontiguous regions of data and describing data so that it can be communicated between processors with different data representations. To do this, MPI uses three values to describe a data buffer: the address, the (MPI) datatype, and the number or count of the items of that datatype. For example, a buffer a containing four C ints is described by the triple "a, 4, MPI_INT." There are predefined MPI datatypes for all of the basic datatypes defined in C, Fortran, and C++. The most common datatypes are shown in Table 8.1.

Table 8.1: The most common MPI datatypes. C and Fortran types on the same row are often but not always the same type. The type MPI_BYTE is used for raw data bytes and does not correspond to any particular datatype. The type MPI_PACKED is used for data that was incrementally packed with the routine MPI_Pack. The C++ MPI datatypes have the same name as the C datatypes but without the MPI_prefix, for example, MPI::INT.

C

Fortran

MPI type

MPI type

int

MPI_INT

INTEGER

MPI_INTEGER

double

MPI_DOUBLE

DOUBLE PRECISION

MPI_DOUBLE_PRECISION

float

MPI_FLOAT

REAL

MPI_REAL

long

MPI_LONG

char

MPI_CHAR

CHARACTER

MPI_CHARACTER

LOGICAL

MPI_LOGICAL

—

MPI_BYTE

—

MPI_BYTE

—

MPI_PACKED

—

MPI_PACKED

Describing the Destination or Source

The destination or source is specified by using the rank of the process. MPI generalizes the notion of destination and source rank by making the rank relative to a group of processes. This group may be a subset of the original group of processes. Allowing subsets of processes and using relative ranks make it easier to use MPI to write component-oriented software (more on this in Section 9.4). The MPI object that defines a group of processes (and a special communication context that will be discussed in Section 9.4) is called a communicator. Thus, sources and destinations are given by two parameters: a rank and a communicator. The communicator MPI_COMM_WORLD is predefined and contains all of the processes started by mpirun or mpiexec. As a source, the special value MPI_ANY_SOURCE may be used to indicate that the message may be received from any rank of the MPI processes in this MPI program.

Selecting among Messages

The "extra" argument for MPI_Send is a nonnegative integer tag value. This tag allows a program to send one extra number with the data. MPI_Recv can use this value either to select which message to receive (by specifying a specific tag value) or to use the tag to convey extra data (by specifying the wild card value MPI_ANY_TAG). In the latter case, the tag value of the received message is stored in the status argument (this is the last parameter to MPI_Recv in the C binding). This is a structure in C, an integer array in Fortran, and a class in C++. The tag and rank of the sending process can be accessed by referring to the appropriate element of status as shown in Table 8.2.

Table 8.2: Accessing the source and tag after an MPI_Recv.

C

Fortran

C++

status.MPI_SOURCE

status(MPI_SOURCE)

status.Get_source()

status.MPI_TAG

status(MPI_TAG)

status.Get_tag()

Determining the Amount of Data Received

The amount of data received can be found by using the routine MPI_Get_count. For example,

     MPI_Get_count( &status, MPI_CHAR, &num_chars );

returns in num_chars the number of characters sent. The second argument should be the same MPI datatype that was used to receive the message. (Since many applications do not need this information, the use of a routine allows the implementation to avoid computing num_chars unless the user needs the value.)

Our example provides a maximum-sized buffer in the receive. It is also possible to find the amount of memory needed to receive a message by using MPI_Probe, as shown in Figure 8.4.

Start Figure 
     char *greeting;
     int num_chars, src;
     MPI_Status status;
     ...
     MPI_Probe( MPI_ANY_SOURCE, 1, MPI_COMM_WORLD, &status );
     MPI_Get_count( &status, MPI_CHAR, &num_chars );
     greeting = (char *)malloc( num_chars );
     src      = status.MPI_SOURCE;
     MPI_Recv( greeting, num_chars, MPI_CHAR,
               src, 1, MPI_COMM_WORLD, &status );
End Figure

Figure 8.4: Using MPI_Probe to find the size of a message before receiving it.

MPI guarantees that messages are ordered, that is, that messages sent from one process to another arrive in the same order in which they were sent and that an MPI_Recv after an MPI_Probe will receive the message that the probe returned information on as long as the same message selection criteria (source rank, communicator, and message tag) are used. Note that in this example, the source for the MPI_Recv is specified as status.MPI_SOURCE, not MPI_ANY_SOURCE, to ensure that the message received is the same as the one about which MPI_Probe returned information.

[2]There are a few exceptions, including MPI_Initialized.

8.2 Manager/Worker Example

We now begin a series of examples illustrating approaches to parallel computations that accomplish useful work. While each parallel application is unique, a number of paradigms have emerged as widely applicable, and many parallel algorithms are variations on these patterns.

One of the most universal is the "manager/worker" or "task parallelism" approach. The idea is that the work that needs to be done can be divided by a "manager" into separate pieces and the pieces can be assigned to individual "worker" processes. Thus the manager executes a different algorithm from that of the workers, but all of the workers execute the same algorithm. Most implementations of MPI (including MPICH2) allow MPI processes to be running different programs (executable files), but it is often convenient (and in some cases required) to combine the manager and worker code into a single program with the structure shown in Figure 8.5.

Start Figure 
 #include "mpi.h"
 
 int main( int argc, char *argv[] )
 {
     int numprocs, myrank;
 
     MPI_Init( &argc, &argv );
     MPI_Comm_size( MPI_COMM_WORLD, &numprocs );
     MPI_Comm_rank( MPI_COMM_WORLD, &myrank );
 
     if ( myrank == 0 )          /* manager process */
         manager_code ( numprocs );
     else                        /* worker process */
         worker_code ( );
     MPI_Finalize( );
     return 0;
 }
End Figure

Figure 8.5: Framework of the matrix-vector multiply program.

Sometimes the work can be evenly divided into exactly as many pieces as there are workers, but a more flexible approach is to have the manager keep a pool of units of work larger than the number of workers and assign new work dynamically to workers as they complete their tasks and send their results back to the manager. This approach, called self-scheduling, works well in the presence of tasks of varying sizes or workers of varying speeds.

We illustrate this technique with a parallel program to multiply a matrix by a vector. (A Fortran version of this same program can be found in [48].) This program is not a particularly good way to carry out this operation, but it illustrates the approach and is simple enough to be shown in its entirety. The program multiplies a square matrix a by a vector b and stores the result in c. The units of work are the individual dot products of the rows of a with the vector b. Thus the manager, code for which is shown in Figure 8.6, starts by initializing a. The manager then sends out initial units of work, one row to each worker. We use the MPI tag on each such message to encode the row number we are sending. Since row numbers start at 0 but we wish to reserve 0 as a tag with the special meaning of "no more work to do," we set the tag to one greater than the row number. When a worker sends back a dot product, we store it in the appropriate place in c and send that worker another row to work on. Once all the rows have been assigned, workers completing a task are sent a "no more work" message, indicated by a message with tag 0.

Start Figure 
 #define SIZE 1000
 #define MIN( x, y ) ((x) < (y) ? x : y)
 
 void manager_code( int numprocs )
 {
     double a[SIZE][SIZE], c[SIZE];
 
     int i, j, sender, row, numsent = 0;
     double dotp;
     MPI_Status status;
 
     /* (arbitrary) initialization of a */
     for (i = 0; i < SIZE; i++ )
         for ( j = 0; j < SIZE; j++ )
             a[i][j] = ( double ) j;
 
     for ( i = 1; i < MIN( numprocs, SIZE ); i++ ) {
         MPI_Send( a[i-1], SIZE, MPI_DOUBLE, i, i, MPI_COMM_WORLD );
         numsent++;
     }
     /* receive dot products back from workers */
     for ( i = 0; i < SIZE; i++ ) {
         MPI_Recv( &dotp, 1, MPI_DOUBLE, MPI_ANY_SOURCE, MPI_ANY_TAG,
                   MPI_COMM_WORLD, &status );
         sender = status.MPI_SOURCE;
         row    = status.MPI_TAG - 1;
         c[row] = dotp;
         /* send another row back to this worker if there is one */
         if ( numsent < SIZE ) {
             MPI_Send( a[numsent], SIZE, MPI_DOUBLE, sender,
                       numsent + 1, MPI_COMM_WORLD );
             numsent++;
         }
         else                    /* no more work */
             MPI_Send( MPI_BOTTOM, 0, MPI_DOUBLE, sender, 0,
                        MPI_COMM_WORLD );
     }
 }
End Figure

Figure 8.6: The matrix-vector multiply program, manager code.

The code for the worker part of the program is shown in Figure 8.7. A worker initializes b, receives a row of a in a message, computes the dot product of that row and the vector b, and then returns the answer to the manager, again using the tag to identify the row. A worker repeats this until it receives the "no more work" message, identified by its tag of 0.

Start Figure 
 void worker_code( void )
 {
     double b[SIZE], c[SIZE];
     int i, row, myrank;
     double dotp;
     MPI_Status status;
 
     for ( i = 0; i < SIZE; i++ ) /* (arbitrary) b initialization */
         b[i] = 1.0;
 
     MPI_Comm_rank( MPI_COMM_WORLD, &myrank );
     if ( myrank <= SIZE ) {
         MPI_Recv( c, SIZE, MPI_DOUBLE, 0, MPI_ANY_TAG,
                   MPI_COMM_WORLD, &status );
         while ( status.MPI_TAG > 0 ) {
             row = status.MPI_TAG - 1;
             dotp = 0.0;
             for ( i = 0; i < SIZE; i++ )
                 dotp += c[i] * b[i];
             MPI_Send( &dotp, 1, MPI_DOUBLE, 0, row + 1,
                       MPI_COMM_WORLD );
             MPI_Recv( c, SIZE, MPI_DOUBLE, 0, MPI_ANY_TAG,
                       MPI_COMM_WORLD, &status );
         }
     }
 }
End Figure

Figure 8.7: The matrix-vector multiply program, worker code.

This program requires at least two processes to run: one manager and one worker. Unfortunately, adding more workers is unlikely to make the job go faster. We can analyze the cost of computation and communication mathematically and see what happens as we increase the number of workers. Increasing the number of workers will decrease the amount of computation done by each worker, and since they work in parallel, this should decrease total elapsed time. On the other hand, more workers mean more communication, and the cost of communicating a number is usually much greater than the cost of an arithmetical operation on it. The study of how the total time for a parallel algorithm is affected by changes in the number of processes, the problem size, and the speed of the processor and communication network is called scalability analysis. We analyze the matrix-vector program as a simple example.

First, let us compute the number of floating-point operations. For a matrix of size n, we have to compute n dot products, each of which requires n multiplications and n - 1 additions. Thus the number of floating-point operations is n ?(n + (n - 1)) = n?/i>(2n-1) = 2n2-n. If Tcalc is the time it takes a processor to do one floating-point operation,[ 3] then the total computation time is (2n2 - n) ?Tcalc. Next, we compute the number of communications, defined as sending one floating-point number. (We ignore for this simple analysis the effect of message lengths; following Section 1.3, we could model these as s + rn, where Tcomm ≈ r.) Leaving aside the cost of communicating b (perhaps it is computed locally in a preceding step), we have to send each row of a and receive back one dot product answer. So the number of floating-point numbers communicated is (n ?n) + n = n2 + n. If Tcomm is the time to communicate one number, we get (n2 + n) ?Tcomm for the total communication time. Thus the ratio of communication time to computation time is

In many computations the ratio of communication to computation can be reduced almost to 0 by making the problem size larger. Our analysis shows that this is not the case here. As n gets larger, the term on the left approaches 1/2. Thus we can expect communication costs to prevent this algorithm from showing good speedups, even on large problem sizes.

The situation is better in the case of matrix-matrix multiplication, which could be carried out by a similar algorithm. We would replace the vectors b and c by matrices, send the entire matrix b to the workers at the beginning of the computation, and then hand out the rows of a as work units, just as before. The workers would compute an entire row of the product, consisting of the dot products of the row of a with all of the column of b, and then return a row of c to the manager.

Let us now do the scalability analysis for the matrix-matrix multiplication. Again we ignore the initial communication of b. The number of operations for one dot product is n + (n + 1) as before, and the total number of dot products calculated is n2. Thus the total number of operations is n2 ?(2n - 1) = 2n3 - n2. The number of numbers communicated has gone up to (n ?n) + (n ?n) = 2n2. So the ratio of communication time to computation time has become

which does tend to 0 as n gets larger. Thus, for large matrices the communication costs play less of a role.

Two other difficulties with this algorithm might occur as we increase the size of the problem and the number of workers. The first is that as messages get longer, the workers waste more time waiting for the next row to arrive. A solution to this problem is to "double buffer" the distribution of work, having the manager send two rows to each worker to begin with, so that a worker always has some work to do while waiting for the next row to arrive.

Another difficulty for larger numbers of processes can be that the manager can become overloaded so that it cannot assign work in a timely manner. This problem can most easily be addressed by increasing the size of the work unit, but in some cases it is necessary to parallelize the manager task itself, with multiple managers handling subpools of work units.

A more subtle problem has to do with fairness: ensuring that all worker processes are fairly serviced by the manager. MPI provides several ways to ensure fairness; see [ 48, Section 7.1.4].

[ 3]The symbol f was used in Section 1.3; we use Tcalc here because of the more prominent role of floating point in this analysis.

8.3 Two-Dimensional Jacobi Example with One-Dimensional Decomposition

A common use of parallel computers in scientific computation is to approximate the solution of a partial differential equation (PDE). One of the most common PDEs, at least in textbooks, is the Poisson equation (here shown in two dimensions):

(8.1)
(8.2)

This equation is used to describe many physical phenomena, including fluid flow and electrostatics. The equation has two parts: a differential equation applied everywhere within a domain F (8.1) and a specification of the value of the unknown u along the boundary of Γ (the notation ∂Γ means "the boundary of Γ"). For example, if this equation is used to model the equilibrium distribution of temperature inside a region, the boundary condition g(x, y) specifies the applied temperature along the boundary, f(x, y) is zero, and u(x, y) is the temperature within the region. To simplify the rest of this example, we will consider only a simple domain Γ consisting of a square (see Figure 8.8).

Click To expand
Figure 8.8: Domain and 9 ?9 computational mesh for approximating the solution to the Poisson problem.

To compute an approximation to u(x, y), we must first reduce the problem to finite size. We cannot determine the value of u everywhere; instead, we will approximate u at a finite number of points (xi,yj) in the domain, where xi = i ?h and yj = j ?h. (Of course, we can define a value for u at other points in the domain by interpolating from these values that we determine, but the approximation is defined by the value of u at the points (xi,yj).) These points are shown as black disks in Figure 8.8. Because of this regular spacing, the points are said to make up a regular mesh. At each of these points, we approximate the partial derivatives with finite differences. For example,

Click To expand

If we now let ui,j stand for our approximation to solution of Equation 8.1 at the

point (xi, yj), we have the following set of simultaneous linear equations for the values of u:

(8.3)

For values of u along the boundary (e.g., at x = 0 or y = 1), the value of the boundary condition g is used. If h = l/(n + 1) (so there are n ?n points in the interior of the mesh), this gives us n2 simultaneous linear equations to solve.

Many methods can be used to solve these equations. In fact, if you have this particular problem, you should use one of the numerical libraries described in Section 12.2. In this section, we describe a very simple (and inefficient) algorithm because, from a parallel computing perspective, it illustrates how to program more effective and general methods. The method that we use is called the Jacobi method for solving systems of linear equations. The Jacobi method computes successive approximations to the solution of Equation 8.3 by rewriting the equation as follows:

(8.4) Click To expand

Each step in the Jacobi iteration computes a new approximation to in terms of the surrounding values of uN:

(8.5) Click To expand

This is our algorithm for computing the approximation to the solution of the Poisson problem. We emphasize that the Jacobi method is a poor numerical method but that the same communication patterns apply to many finite difference, volume, or element discretizations solved by iterative techniques.

In the uniprocessor version of this algorithm, the solution u is represented by a two-dimensional array u[max_n] [max_n], and the iteration is written as follows:

    double u[NX+2][NY+2], u_new[NX+2][NY+2], f[NX+2][NY+2];
    int    i, j;
    ...
    for (i=1;i<=NX;i++)
       for (j=1;j<=NY;j++)
          u_new[i][j] = 0.25 * (u[i+1][j] + u[i-1][j] +
                                u[i][j+1] + u[i][j-l] - h*h*f[i][j]);

Here, we let u[0][j], u[n+1][j], u[i][0], and u[i][n+1] hold the values of the boundary conditions g (these correspond to u(0,y), u(1, y), u(x, 0), and u(x, 1) in Equation 8.1). To parallelize this method, we must first decide how to decompose the data structure u and u_new across the processes. Many possible decompositions exist. One of the simplest is to divide the domain into strips as shown in Figure 8.8.

Let the local representation of the array u be ulocal; that is, each process declares an array ulocal that contains the part of u held by that process. No process has all of u; the data structure representing u is decomposed among all of the processes. The code that is used on each process to implement the Jacobi method is

    double ulocal_new[NLOCAL][NY+2];
    ...
    for (i=i_start;i<=i_end;i++)
      for (j=1;j<=NY;j++)
        ulocal_new[i-i_start][j] =
           0.25 * (ulocal[i-i_start+1][j] + ulocal[i-i_start-1][j] +
                   ulocal[i-i_start][j+1] + ulocal[i-i_start][j-1] -
                   h*h*flocal[i-i_start][j]);

where i_start and i_end describe the strip on this process (in practice, the loop would be from zero to i_end-i_start; we use this formulation to maintain the correspondence with the uniprocessor code). We have defined ulocal so that ulocal[0][j] corresponds to u[i_start][j] in the uniprocessor version of this code. Using variable names such as ulocal that make it obvious which variables are part of a distributed data structure is often a good idea.

From this code, we can see what data we need to communicate. For i=i_start we need the values of u[i_start-1][j] for j between 1 and NY, and for i=i_end we need u[i_end+1][j] for the same range of j. These values belong to the adjacent processes and must be communicated. In addition, we need a location in which to store these values. We could use a separate array, but for regular meshes the most common approach is to use ghost or halo cells, where extra space is set aside in the ulocal array to hold the values from neighboring processes. In this case, we need only a single column of neighboring data, so we will let u_local[1][j] correspond to u[i_start][j]. This changes the code for a single iteration of the loop to

    exchange_nbrs( ulocal, i_start, i_end, left, right );
    for (i_local=1; i_local<=i_end-i_start+1; i_local++)
      for (j=1; j<=NY; j++)
 
 
       ulocal_new[i_local][j] =
          0.25 * (ulocal[i_local+1][j] + ulocal[i_local-1][j] +
                  ulocal[i_local][j+1] + ulocal[i_local][j-1] -
                  h*h*flocal[i_local][j]);

where we have converted the i index to be relative to the start of ulocal rather than u. All that is left is to describe the routine exchange_nbrs that exchanges data between the neighboring processes. A very simple routine is shown in Figure 8.9.

Start Figure 
 void exchange_nbrs( double ulocal[][NY+2], int i_start, int i_end,
                     int left, int right )
 {
     MPI_Status status;
     int c;
 
     /* Send and receive from the left neighbor */
     MPI_Send( &ulocal[1][1], NY, MPI_DOUBLE, left, 0,
               MPI_COMM_WORLD );
     MPI_Recv( &ulocal[0][1], NY, MPI_DOUBLE, left, 0,
               MPI_COMM_WORLD, &status );
 
     /* Send and receive from the right neighbor */
     c = i_end - i_start + 1;
     MPI_Send( &ulocal[c][1], NY, MPI_DOUBLE, right, 0,
               MPI_COMM_WORLD );
     MPI_Recv( &ulocal[c+1][1], NY, MPI_DOUBLE, right, 0,
               MPI_COMM_WORLD, &status );
 }
End Figure

Figure 8.9: A simple version of the neighbor exchange code. See the text for a discussion of the limitations of this routine.

We note that ISO/ANSI C (unlike Fortran) does not allow runtime dimensioning of multidimensional arrays. To keep these examples simple in C, we use compile-time dimensioning of the arrays. An alternative in C is to pass the arrays as one-dimensional arrays and compute the appropriate offsets.

The values left and right are used for the ranks of the left and right neighbors, respectively. These can be computed simply by using the following:

     int rank, size, left, right;
     ...
 
 
     MPI_Comm_rank( MPI_COMM_WORLD, &rank );
     MPI_Comm_size( MPI_COMM_WORLD, &size  );
     left = rank - 1;
     right = rank + 1;
     if (left < 0)      left  = MPI_PROC_NULL;
     if (right >= size) right = MPI_PROC_NULL;

The special rank MPI_PROC_NULL indicates the edges of the mesh. If MPI_PROC_NULL is used as the source or destination rank in an MPI communication call, the operation is ignored. MPI also provides routines to compute the neighbors in a regular mesh of arbitrary dimension and to help an application choose a decomposition that is efficient for the parallel computer.

The code in exchange_nbrs will work with most MPI implementations for small values of n but, as described in Section 9.3, is not good practice (and will fail for values of NY greater than an implementation-defined threshold). A better approach in MPI is to use the MPI_Sendrecv routine when exchanging data between two processes, as shown in Figure 8.10.

Start Figure 
 /* Better exchange code.  */
 void exchange_nbrs( double ulocal[][NY+2], int i_start, int i_end,
                     int left, int right )
 {
     MPI_Status status;
     int c;
 
     /* Send and receive from the left neighbor */
     MPI_Sendrecv( &ulocal[1][1], NY, MPI_DOUBLE, left, 0,
                   &ulocal[0][1], NY, MPI_DOUBLE, left, 0,
                   MPI_COMM_WORLD, &status );
 
     /* Send and receive from the right neighbor */
     c = i_end - i_start + 1;
     MPI_Sendrecv( &ulocal[c][1], NY, MPI_DOUBLE, right, 0,
                   &ulocal[c+1][1], NY, MPI_DOUBLE, right, 0,
                   MPI_COMM_WORLD, &status );
 }
End Figure

Figure 8.10: A better version of the neighbor exchange code.

In Sections 9.3 and 9.7, we discuss other implementations of the exchange routine that can provide higher performance. MPI support for more scalable decompositions of the data is described in Section 9.3.2.

8.4 Collective Operations

A collective operation is an MPI function that is called by all processes belonging to a communicator. (If the communicator is MPI_COMM_WORLD, this means all processes, but MPI allows collective operations on other sets of processes as well.) Collective operations involve communication and also sometimes computation, but since they describe particular patterns of communication and computation, the MPI implementation may be able to optimize them beyond what is possible by expressing them in terms of MPI point-to-point operations such as MPI_Send and MPI_Recv. The patterns are also easier to express with collective operations.

Here we introduce two of the most commonly used collective operations and show how the communication in a parallel program can be expressed entirely in terms of collective operations with no individual MPI_Sends or MPI_Recvs at all. The program shown in Figure 8.11 computes the value of π by numerical integration. Since

Start Figure 
 #include "mpi.h"
 #include <stdio.h>
 #include <math.h>
 double f(double a) { return (4.0 / (1.0 + a*a)); }
 
 int main(int argc,char *argv[])
 {
   int n, myid, numprocs, i;
   double PI25DT = 3.141592653589793238462643;
   double mypi, pi, h, sum, x;
   double startwtime = 0.0, endwtime;
 
   MPI_Init(&argc,&argv);
   MPI_Comm_size(MPI_COMM_WORLD,&numprocs);
   MPI_Comm_rank(MPI_COMM_WORLD,&myid);
   if (myid == 0) {
       startwtime = MPI_Wtime();
       n = atoi(argv[1]);
   }
   MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
   h   = 1.0 / (double) n;
   sum = 0.0;
   for (i = myid + 1; i <= n; i += numprocs) {
       x = h * ((double)i - 0.5);
       sum += f(x);
   }
   mypi = h * sum;
   MPI_Reduce(&mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
   if (myid == 0) {
       endwtime = MPI_Wtime();
       printf("pi is approximately %.16f, Error is %.16f\n",
              pi, fabs(pi - PI25DT));
       printf("wall clock time = %f\n", endwtime-startwtime);
   }
   MPI_Finalize();
   return 0;
 }
End Figure

Figure 8.11: Computing π using collective operations.
Click To expand

we can compute π by integrating the function f(x) = 4/(l + x2) from 0 to 1. We compute an approximation by dividing the interval [0,1] into some number of subintervals and then computing the total area of these rectangles by having each process compute the areas of some subset. We could do this with a manager/worker algorithm, but here we preassign the work. In fact, each worker can compute its set of tasks, and so the "manager" can be a worker, too, instead of just managing the pool of work. The more rectangles there are, the more work there is to do and the more accurate the resulting approximation of π is. To experiment, let us make the number of subintervals a command-line argument. (Although the MPI standard does not guarantee that any process receive command-line arguments, in most implementations, especially for Beowulf clusters, one can assume that at least the process with rank 0 can use argc and argv, although they may not be meaningful until after MPI_Init is called.) In our example, process 0 sets n, the number of subintervals, to argv[1]. Once a process knows n, it can claim approximately of the work by claiming every nth rectangle, starting with the one numbered by its own rank. Thus, process j computes the areas of rectangles j , j + n , j + 2n, and so on.

Not all MPI implementations make the command-line arguments available to all processes, however, so we start by having process 0 send n to each of the other processes. We could have a simple loop, sending n to each of the other processes one at a time, but this is inefficient. If we know that the same message is to be delivered to all the other processes, we can ask the MPI implementation to do this in a more efficient way than with a series of MPI_Sends and MPI_Recvs.

Broadcast (MPI_Bcast) is an example of an MPI collective operation. A collective operation must be called by all processes in a communicator. This allows an implementation to arrange the communication and computation specified by a collective operation in a special way. In the case of MPI_Bcast, an implementation is likely to use a tree of communication, sometimes called a spanning tree, in which process 0 sends its message to a second process, then both processes send to two more, and so forth. In this way most communication takes place in parallel, and all the messages have been delivered in log2 n steps.

The precise semantics of MPI_Bcast is sometimes confusing. The first three arguments specify a message with (address, count, datatype) as usual. The fourth argument (called the root of the broadcast) specifies which of the processes owns the data that is being sent to the other processes. In our case it is process 0. MPI_Bcast acts like an MPI_Send on the root process and like an MPI_Recv on all the other processes, but the call itself looks the same on each process. The last argument is the communicator that the collective call is over. All processes in the communicator must make this same call. Before the call, n is valid only at the root; after MPI_Bcast has returned, all processes have a copy of the value of n.

Next, each process, including process 0, adds up the areas of its rectangles into the local variable mypi. Instead of sending these values to one process and having that process add them up, however, we use another collective operation, MPI_Reduce. MPI_Reduce performs not only collective communication but also collective computation. In the call

     MPI_Reduce( &mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0,
                 MPI_COMM_WORLD);

the sixth argument is again the root. All processes call MPI_Reduce, and the root process gets back a result in the second argument. The result comes from performing an arithmetic operation, in this case summation (specified by the fifth argument), on the data items on all processes specified by the first, third, and fourth arguments.

Process 0 concludes by printing out the answer, the difference between this approximation and a previously computed accurate value of π, and the time it took to compute it. This illustrates the use of MPI_Wtime.

MPI_Wtime returns a double-precision floating-point number of seconds. This value has no meaning in itself, but the difference between two such values is the wall-clock time between the two calls. Note that calls on two different processes are not guaranteed to have any relationship to one another, unless the MPI implementation promises that the clocks on different processes are synchronized (see MPI_WTIME_IS_GLOBAL in any of the MPI books).

The routine MPI_Allreduce computes the same result as MPI_Reduce but returns the result to all processes, not just the root process. For example, in the Jacobi iteration, it is common to use the two-norm of the difference between two successive iterations as a measure of the convergence of the solution.

     ...
     norm2local = 0.0;
     for (ii=1; ii<i_end-i_start+1; ii++)
         for (jj=1; jj<NY; jj++)
             norm2local += ulocal[ii][jj] * ulocal[ii][jj];
     MPI_Allreduce( &norm2local, &norm2, 1, MPI_DOUBLE,
                    MPI_COMM_WORLD, MPI_SUM );
     norm2 = sqrt( norm2 );

Note that MPI_Allreduce is not a routine for computing the norm of a vector. It merely combines values contributed from each process in the communicator.

8.5 Parallel Monte Carlo Computation

One of the types of computation that is easiest to parallelize is the Monte Carlo family of algorithms. In such computations, a random number generator is used to create a number of independent trials. Statistics done with the outcomes of the trials provide a solution to the problem.

We illustrate this technique with another computation of the value of π. If we select points at random in the unit square [0, 1] ?[0, 1] and compute the percentage of them that lies inside the quarter circle of radius 1, then we will be approximating . (See [48] for a more detailed discussion together with an approach that does not use a parallel random number generator.) We use the SPRNG parallel random number generator (sprng.cs.fsu.edu). The code is shown in Figure 8.12.

Start Figure 
 #include "mpi.h"
 #include <stdio.h>
 #define SIMPLE_SPRNG        /* simple interface  */
 #define USE_MPI             /* use MPI           */
 #include "sprng.h"          /* SPRNG header file */
 #define BATCHSIZE 1000000
 
 int main( int argc, char *argv[] )
 {
     int i, j, numin = 0, totalin, total, numbatches, rank, numprocs;
     double x, y, approx, pi = 3.141592653589793238462643;
 
     MPI_Init( &argc, &argv );
     MPI_Comm_size( MPI_COMM_WORLD, &numprocs );
     MPI_Comm_rank( MPI_COMM_WORLD, &rank );
     if ( rank == 0 ) {
         numbatches = atoi( argv[1] );
     }
     MPI_Bcast( &numbatches, 1, MPI_INT, 0, MPI_COMM_WORLD );
     for ( i = 0; i < numbatches; i++ ) {
         for ( j = 0; j < BATCHSIZE; j++) {
             x = sprng( ); y = sprng( );
             if ( x * x + y * y < 1.0 )
                 numin++;
         }
         MPI_Reduce( &numin, &totalin, 1, MPI_INT, MPI_SUM, 0,
                     MPI_COMM_WORLD );
         if ( rank == 0 ) {
             total = BATCHSIZE * ( i + 1 ) * numprocs;
             approx = 4.0 * ( (double) totalin / total );
             printf( "pi = %.16f; error = %.16f, points = %d\n",
                     approx, pi - approx, total );
         }
     }
     MPI_Finalize( );
     return 0;
 }
End Figure

Figure 8.12: — Computing π using the Monte Carlo method.

The defaults in SPRNG make it extremely easy to use. Calls to the sprng function return a random number between 0.0 and 1.0, and the stream of random numbers on the different processes is independent. We control the grain size of the parallelism by the constant BATCHSIZE, which determines how much computation is done before the processes communicate. Here a million points are generated, tested, and counted before we collect the results to print them. We use MPI_Bcast to distribute the command-line argument specifying the number of batches, and we use MPI_Reduce to collect at the end of each batch the number of points that fell inside the quarter circle, so that we can print the increasingly accurate approximations to π.

8.6 MPI Programming without MPI

One of the major strengths of MPI is the support that MPI provides for building libraries of useful software. These libraries often eliminate the need for explicit programming in MPI; in cases where no suitable library exists, MPI's design encourages the use of modern software engineering techniques in creating application-specific support libraries. Some of the available libraries are shown in Table 9.1; Chapter 12 discusses some of the more important libraries in more detail. To illustrate the power of libraries in MPI, this section shows several programs that solve partial differential equations without the explicit use of MPI. These are still MPI programs, however, and must be run using mpiexec just like other MPI programs.

8.6.1 A Poisson Solver

Section 8.3 presented an MPI code that implemented the Jacobi method for solving a simple partial differential equation. This example provided a good introduction to MPI but is not meant as an example of how to solve differential equations in parallel with MPI. For that task, one or more parallel libraries should be used. Figure 8.13 shows a short code for solving two-dimentional Poisson problems on a regular mesh. This code makes very heavy use of two libraries:

  • PETSc [ 9, 10, 8] is a library designed to solve in parallel linear and nonlinear equations that arise from PDEs. PETSc uses MPI.

  • "regmesh" is an application-specific library written to simplify the use of PETSc for regular mesh discritizations of elliptic partial differential equations. This library makes no explicit MPI calls; instead, all parallelism is handled through PETSc.

Start Figure 
 #include <math.h>
 #include "petsc.h"
 #include "regmesh.h"
 
 /* This function is used to define the right-hand side of the
    Poisson equation to be solved */
 double func( double x, double y )
 {
     return sin(x)*sin(y);
 }
 
 int main( int argc, char *argv[] )
 {
     SLES    sles;
     RegMesh g;
     Mat     m;
     Vec     b, x;
     Viewer  viewer;
     int     its;
 
     PetscInitialize( &argc, &argv, 0, 0 );
 
     g = Create2dDistributedArray( n, n, 0.0, 1.0, 0.0, 1.0 );
     m = ApplyStencilTo2dDistributedArray( g, REGMESH_LAPLACIAN );
     b = SetVectorFromFunction( g, (RegMeshFunc)func );
     VecDuplicate( b, &x );
     SLESCreate( PETSC_COMM_WORLD, &sles );
     SLESSetOperators( sles, m, m, DIFFERENT_NONZERO_PATTERN);
     SLESSetFromOptions( sles );
     SLESSolve( sles, b, x, &its );
     PetscViewerNetcdfOpen( PETSC_COMM_WORLD, "solution.nc",
                            PETSC_NETCDF_CREATE, &viewer );
     MeshDAView( g, viewer );
     RegMeshDestroy( g ); MatDestroy( m ); VecDestroy( b ); VecDestroy( x );
     SLESDestroy( sles );
     PetscFinalize( );
     return 0;
 }
End Figure

Figure 8.13: A parallel Poisson solver that exploits two libraries written with MPI.

The routines in this example perform the following operations:

  • PetscInitialize — Initialize the PETSc library

  • Create2dDistributedArray — Create a handle (g) to a structure that defines a two-dimensional mesh of size n? on the unit square. This mesh is distributed across all processes. This routine is from regmesh.

  • ApplyStencilTo2dDistributedArray — Create the sparse matrix (returned as the value m) by applying a disretization stencil to the mesh g. The discretization is predefined and is the same one described in Section 8.3. This routine is from regmesh but returns a handle to a PETSc matrix.

  • SetVectorFromFunction — Return the vector representing the right-hand side of the problem by applying a function func to the mesh g. This routine is from regmesh but returns a handle to a PETSc vector.

  • SLESCreate — Create a PETSc context for solving a linear system of equations. This is a handle for the internal structure that PETSc uses to hold all of the information, such as the choice of algorithm, used to solve a linear system of equations.

  • SLESSetOperators — Define the linear system to solve by specifying the matrices. This routine allows several variations of specification; this example uses the most common.

  • SLESSetFromOptions — Set the various parameter choices from the command line and a defaults file. This lets the user choose the iterative method and pre-conditioner at run time by using command-line arguments.

  • SLESSolve — Solve the linear system Ax = b, returning the solution in the PETSc vector x. This is a PETSc routine.

  • PetscViewerNetcdfOpen — Create a "viewer" by which a PETSc vector can be written to a file (here 'solution.nc') using the community-standard NetCDF format [95]. This is a PETSc routine.

  • MeshDAView — Output the solution using the viewer. This makes use of the PETSc "distributed array" structure as well as other data from the regmesh g.

  • xxxDestroy — Free the space used by the mesh, vector, and matrix structures, as well as the linear equation solver.

An advantage of this approach to writing parallel programs is that it allows the application programmer to take advantage of the best numerical algorithms and parallel tools. For example, the command-line

     mpiexec -n 64 poisson -pc_type=ilu -ksp_type=gmres

runs this example on 64 processors, using the GMRES iterative method with a block incomplete factorization preconditioner. Changing the choice of iterative method or preconditioner is accomplished by simply changing the command-line arguments.

In addition, this example includes output of the solution, using parallel I/O into a file (when supported by a parallel file system such as PVFS, described in Chapter 19). Further, this file is written in a standard format called NetCDF; a wide variety of tools exist for postprocessing this file, including programs to display the contents graphically.

Regmesh is a specialized library designed to simplify the creation of parallel programs that work with regular meshes. More importantly, Regmesh is an example of structuring an application so that the important operations are organized into logical units.

8.6.2 Solving a Nonlinear Partial Differential Equation

To further illustrate the power of MPI libraries, Figure 8.14 shows the main program for solving the problem

Start Figure 
 #include "petsc.h"
 /* User-defined data describing the problem */
 typedef struct {
    DA            da;             /* distributed array data structure */
    double        param;          /* test problem parameter */
 } AppCtx;
 extern int FormFunctionLocal(DALocalInfo*,double**,double**,AppCtx*);
 extern int FormJacobianLocal(DALocalInfo*,double**,Mat,AppCtx*);
 int main(int argc,char *argv[])
 {
   SNES     snes;     /* nonlinear solver */
   Vec      x,r;      /* solution, residual vectors */
   Mat      A,J;      /* Jacobian matrix */
   AppCtx   user;     /* user-defined work context */
   int      its;      /* iterations for convergence */
 
   PetscInitialize(&argc,&argv,(char *)0,help);
   user.param = 6.0;
   SNESCreate(PETSC_COMM_WORLD,&snes);
   DACreate2d(PETSC_COMM_WORLD,DA_NONPERIODIC,DA_STENCIL_STAR,
                     -4,-4,PETSC_DECIDE,PETSC_DECIDE,
                     1,1,PETSC_NULL,PETSC_NULL,&user.da);
   DACreateGlobalVector(user.da,&x);
   VecDuplicate(x,&r);
   DASetLocalFunction(user.da,(DALocalFunction1)FormFunctionLocal);
   DASetLocalJacobian(user.da,(DALocalFunction1)FormJacobianLocal);
   SNESSetFunction(snes,r,SNESDAFormFunction,&user);
   DAGetMatrix(user.da,MATMPIAIJ,&J);
   A    = J;
   SNESSetJacobian(snes,A,J,SNESDAComputeJacobian,&user);
   SNESSetFromOptions(snes);
   FormInitialGuess(&user,x);
   SNESSolve(snes,x,&its);
   PetscPrintf(PETSC_COMM_WORLD,"Number of Newton iterations = %d\n",its);
 
   MatDestroy(J); VecDestroy(x); VecDestroy(r); SNESDestroy(snes);
   DADestroy(user.da);
   PetscFinalize();
   return 0;
 }
End Figure

Figure 8.14: The main program in a high-level program to solve a nonlinear partial differential equation using PETSc.

∇2u

=

-λeu on Ω = [0, 1] ?[0, 1]

u

=

0 on the boundary of Ω.

This problem is the Bratu problem. This code uses only PETSc and, as a result, is somewhat longer. Not included in this figure are some of the routines for computing the Jacobian elements, evaluating the function, setting the initial guess, or checking for errors. A complete version of this example is included as 'src/snes/examples/tutorials/ex5.c' in the PETSc distribution. Even this program is only a few hundred lines, including extensive comments.

These two examples show that tools are available that make writing parallel programs using MPI relatively easy, as long as high-quality libraries are available for the operations needed by an application. Fortunately, in many areas of science and engineering, such libraries are available, and more are added all the time.

8.7 Installing MPICH2 under Linux

The MPICH implementation of MPI [47] is one of the most popular versions of MPI. Recently, MPICH was completely rewritten; the new version is called MPICH2 and includes all of MPI, both MPI-1 and MPI-2. In this section we describe how to obtain, build, and install MPICH2 on a Beowulf cluster. We then describe how to set up an MPICH2 environment in which MPI programs can be compiled, executed, and debugged. We recommend MPICH2 for all Beowulf clusters. Original MPICH is still available but is no longer being developed.

8.7.1 Obtaining and Installing MPICH2

The current version of MPICH2 is available at www.mcs.anl.gov/mpi/mpich.[ 4] From there one can download a gzipped tar file containing the complete MPICH2 distribution, which contains

  • all source code for MPICH2;

  • configure scripts for building MPICH2 on a wide variety of environments, including Linux clusters;

  • simple example programs like the ones in this chapter;

  • MPI compliance test programs; and

  • the MPD parallel process management system.

MPICH2 is architected so that a number of communication infrastructures can be used. These are called "devices." The device that is most relevant for the Beowulf environment is the channel device (also called "ch3" because it is the third version of the channel approach for implementing MPICH); this supports a variety of communication methods and can be built to support the use of both TCP over sockets and shared memory. In addition, MPICH2 uses a portable interface to process management systems, providing access both to external process managers (allowing the process managers direct control over starting and running the MPI processes) and to the MPD scalable process manager that is included with MPICH2. To run your first MPI program, carry out the following steps (assuming a C-shell):

  1. Download mpich2.tar.gz from www.mcs.anl.gov/mpi/mpich or from ftp://ftp.mcs.anl.gov/pub/mpi/mpich2.tar.gz

  2. tar xvfz mpich2.tar.gz ; cd mpich2-1.0

  3. configure <configure options> >& configure.log. Most users should specify a prefix for the installation path when configuring:

         configure --prefix=/usr/local/mpich2-1.0 >& configure.log

    By default, this creates the channel device for communication with TCP over sockets.

  4. make >& make.log

  5. make install >& install.log

  6. Add the '<prefix>/bin' directory to your path; for example, for tcsh, do

         setenv PATH <prefix>/bin:$PATH
     rehash

  7. cd examples

  8. make cpi

  9. Before running your first program, you must start the mpd process manager. To run on a single node, you need only do mpd -d &. See Section 8.7.3 for details on starting mpd on multiple nodes.

  10. mpiexec -n 4 cpi (if '.' is not in your path, you will need to use mpiexec -n 4 ./cpi).

8.7.2 Building MPICH2 for SMP Clusters

To build MPICH2 to support SMP clusters and to use shared-memory to communicate data between processes on the same node, configure MPICH2 with the additional option --with-device=ch3:ssm, as in

    configure --with-device=ch3:ssm --prefix=/usr/local/mpich2-1.0

In a system that contains both SMP nodes and uniprocessor nodes, or if you want an executable that can run on both kinds of nodes, use this version of the ch3 device.

8.7.3 Starting and Managing MPD

Running MPI programs with the MPD process manager assumes that the mpd daemon is running on each machine in your cluster. In this section we describe how to start and manage these daemons. The mpd and related executables are built when you build and install MPICH2 with the default process manager. The code for the MPD demons are found in '<prefix-directory>/bin', which you should ensure is in your path. A set of MPD daemons can be started with the command

     mpichboot <file> <num>

where file is the name of a file containing the host names of your cluster and num is the number of daemons you want to start. The startup script uses ssh to start the daemons, but if it is more convenient, they can be started in other ways. The first one can be started with mpd -t. The first daemon, started in this way, will print out the port it is listening on for new mpds to connect to it. Each subsequent mpd is given a host and port to connect to. The mpichboot script automates this process. At any time you can see what mpds are running by using mpdtrace.

An mpd is identified by its host and a port. A number of commands are used to manage the ring of mpds:

  • mpdhelp prints a short description of the available mpd commands.

  • mpdcleanup cleans up mpd if a problem occurred. For example, it can repair the local Unix socket that is used to communicate with the MPD system if the MPD ring crashed.

  • mpdtrace causes each mpd in the ring to respond with a message identifying itself and its neighbors.

  • mpdallexit causes all mpds to exit gracefully.

  • mpdlistjobs lists active jobs for the user managed by mpds in ring. With the command-line option -a or --all, lists the jobs for all user4s.

  • mpdkilljob job_id kills all of the processes of the specified job.

  • mpdsigjob sigtype job_id delivers the specified signal to the specified job. Signals are specified using the name of the signal, e.g., SIGSTOP.

Several options control the behavior of the daemons, allowing them to be run either by individual users or by root without conflicts. The most important is

  • -d background or "daemonize"; this is used to start an mpd daemon that will run without being connected to a terminal session.

8.7.4 Running MPICH2 Jobs under MPD

MPICH2 jobs are run under the MPD process manager by using the mpiexec command. MPD's mpiexec is consistent with the specification in the MPI standard and also offers a few extensions, such as passing of environment variables to individual MPI processes. An example of the simplest way to run an MPI program is

     mpiexec -n 32 cpi

which runs the MPI program cpi with 32 processes and lets the MPD process manager choose which hosts to run the processes on. Specific hosts and separate executables can be specified:

     mpiexec -n 1 -host node0 manager : -n 1 -host nodel worker

A configuration file can be used when a command line in the above format would be too long:

     mpiexec -configfile multiblast.cfg

where the file 'multiblast.cfg' contains

     -n 1 -host node0 blastmanager
     -n 1 -host nodel blastworker
     ...
     -n 1 -host node31 blastworker

One can use

     mpiexec -help

to discover all the possible command-line arguments for mpiexec.

The program mpiexec runs in a separate (non-MPI) process that starts the MPI processes running the specified executable. It serves as a single-process representative of the parallel MPI processes in that signals sent to it, such as ^Z and ^C are conveyed by the MPD system to all the processes. The output streams stdout and stderr from the MPI processes are routed back to the stdout and stderr of mpiexec. As in most MPI implementations, mpirun's stdin is routed to the stdin of the MPI process with rank 0.

8.7.5 Debugging MPI Programs

Debugging parallel programs is notoriously difficult. Parallel programs are subject not only to the usual kinds of bugs but also to new kinds having to do with timing and synchronization errors. Often, the program "hangs," for example when a process is waiting for a message to arrive that is never sent or is sent with the wrong tag. Parallel bugs often disappear precisely when you add code to try to identify the bug, a particularly frustrating situation. In this section we discuss three approaches to parallel debugging.

The printf Approach

Just as in sequential debugging, you often wish to trace interesting events in the program by printing trace messages. Usually you wish to identify a message by the rank of the process emitting it. This can be done explicitly by putting the rank in the trace message. As noted above, using the "line labels" option (-l) with mpirun in the ch_p4mpd device in MPICH adds the rank automatically.

Using a Commercial Debugger

The TotalView debugger from Etnus, Ltd. [119] runs on a variety of platforms and interacts with many vendor implementations of MPI, including MPICH on Linux clusters. For the ch_p4 device you invoke TotalView with

     mpirun -tv <other arguments>

and with the ch_p4mpd device you use

     totalview mpirun <other arguments>

That is, again mpirun represents the parallel job as a whole. TotalView has special commands to display the message queues of an MPI process. It is possible to attach TotalView to a collection of processes that are already running in parallel; it is also possible to attach to just one of those processes.

Check the documentation on how to use Totalview with mpiexec in MPICH2, or with other implementations of MPI.

8.7.6 Other Compilers

MPI implementations are usually configured and built by using a particular set of compilers. For example, the configure script in the MPICH implementation determines many of the characteristics of the compiler and the associated runtime libraries. As a result, it can be difficult to use a different C or Fortran compiler with a particular MPI implementation. This can be a problem for Beowulf clusters because several different compilers are commonly used.

The compilation scripts (e.g., mpicc) accept an argument to select a different compiler. For example, if MPICH is configured with gcc but you want to use pgcc to compile and build an MPI program, you can use

     mpicc -cc=pgcc -o hellow hellow.c
     mpif77 -fc=pgf77 -o hellowf hellowf.f

This works as long as both compilers have similar capabilities and properties. For example, they must use the same lengths for the basic datatypes, and their runtime libraries must provide the functions that the MPI implementation requires. If the compilers are similar in nature but require slightly different libraries or compiler options, then a configuration file can be provided with the -config=name option:

     mpicc -config=pgcc -o hellow hellow.c

Details on the format of the configuration files can be found in the MPICH installation manual.

The same approach can be used with Fortran as for C. If, however, the Fortran compilers are not compatible (for example, they use different values for Fortran .true. and .false.), then you must build new libraries. MPICH2 provides a way to build just the necessary Fortran support. See the MPICH2 installation manual for details.

[4]As this chapter is being written, the current version of MPICH2 is 0.93, and the current verison of MPICH is 1.2.5.

8.9 MPI Implementations for Clusters

Many implementations of MPI are available for clusters; Table 8.3 lists some of the available implementations. These range from commercially supported software to supported, freely available software to distributed research project software.

Table 8.3: Some MPI implementations for Linux.

Name

URL

BeoMPI

www.scyld.com

LAM/MPI

www.lam-mpi.org

MPICH

www.mcs.anl.gov/mpi/mpich

MPICH-GM

www.myricom.com

MPICH-G2

www.niu.edu/mpi

MPICH-Madeleine

dept-info.labri.u-bordeaux.fr/~mercier/mpi.html

MPICH-V

www.lri.fr/~gk/MPICH-V/

MPI/GAMMA

www.disi.unige.it/project/gamma/mpigamma/

MPI/Pro

www.mpi-softtech.com

MP-MPICH

www.lfbs.rwth-aachen.de/mp-mpich/

MVABICH

nowlab.cis.ohio-state.edu/projects/mpi-iba/

MVICH

www.nersc.gov/research/ftg/mvich/

ScaMPI

www.scali.com

Chapter 10: Parallel Virtual Machine

Overview

Al Geist

PVM (Parallel Virtual Machine) was first released in the early 1990s as an outgrowth of an ongoing computing research project involving Oak Ridge National Laboratory, the University of Tennessee, and Emory University. The general goals of this project are to investigate issues in, and develop solutions for, heterogeneous distributed computing. PVM was one of the solutions. PVM was designed to be able to combine computers having different operating systems, different data representations (both number of bits and byte order), different architectures (multiprocessor, single processor, and even supercomputers), different languages, and different networks and have them all work together on a single computational problem.

PVM existed before Beowulf clusters were invented and in fact was the software used to run applications on the first Beowulf clusters. Today, both PVM and MPICH are often included in software distributions for Beowulf clusters.

The basic idea behind PVM was to create a simple software package that could be loaded onto any collection of computers that would make the collection appear to be a single, large, distributed-memory parallel computer. PVM provides a way for aggregating the power and memory of distributed compute resources. Today this is called Grid computing. In the early 1990s PVM was used to do a number of early Grid experiments, including creating the first international Grid by combining supercomputers in the United Kingdom with supercomputers in the United States, creating a Grid that combined 53 Cray supercomputers across the United States into a single super-supercomputer, and connecting the two largest parallel computers in the world into a 4,000-processor system to solve a nanotechnology problem that eventually led to the high-capacity hard drives used in today's PCs. In 1990 PVM was used for an application in high-temperature superconductivity; the application won a Gordon Bell Prize in supercomputing—the first of many Gordon Bell prizes won by researchers using PVM.

But PVM's real contribution to science and computing is not in supercomputing. PVM's reliability and ease of use made this software package very popular for hooking together a network of workstations or a pile of PCs into a virtual parallel computer that gave PVM users several times more power than they would have otherwise. With tens of thousands of users, PVM was so popular that it became a de facto standard for heterogeneous distributed computing worldwide.

PVM still remains popular, particularly for applications that require fault tolerance. For example, PVM is used to provide fault tolerance to the Globus Toolkit Grid Information Services for the DOE Science Grid. PVM is also used on clusters running the Genomics Integrated Supercomputer Toolkit to provide 24/7 availability despite faults in the clusters.

The tiny 1.5 Mbyte PVM software package is an integrated set of software tools and libraries that emulates a general-purpose, dynamic, heterogeneous parallel computing environment on a set of computers that are connected by a network. The network can be the Internet (Grid computing) or a dedicated local network (cluster). One use of PVM today is to combine multiple Beowulf clusters at a site into a Grid of clusters as shown in Figure 10.1.

Click To expand
Figure 10.1: PVM used to create a Grid of clusters.

The PVM library includes functions to add computers to the parallel virtual machine, spawn tasks on these computers, and exchange data between tasks through message passing. This chapter provides detailed descriptions and examples of the basic concepts and methodologies involved in using PVM on clusters as well as its use as a means to combine multiple clusters into a Grid of clusters. The next chapter details the special functions in PVM for use in fault tolerant and dynamic environments.

10.1 The PVM System

The PVM system is composed of two parts. The first part is a daemon, called pvmd3 and sometimes abbreviated pvmd, that must be installed on all the computers making up the virtual machine. (An example of a daemon program is the mail program that runs in the background and handles all the incoming and outgoing electronic mail on a computer.) The daemon pvmd3 is designed so any user with a valid login can install this daemon on a machine. To run a PVM application, you first create a virtual machine by starting up PVM ( Section 10.3.2 details how this is done). Multiple users can configure virtual machines that overlap the same cluster nodes, and each user can execute several applications simultaneously on his own virtual machine.

The second part of the system is a library of PVM interface routines. It contains a functionally complete repertoire of primitives that are needed for cooperation between tasks of an application. This library contains user-callable routines for fault detection, message passing, spawning processes, coordinating tasks, and modifying the virtual machine.

The Parallel Virtual Machine computing environment is based on the following concepts:

  • User-configured host pool: The application's parallel tasks execute on a set of machines that are selected by the user for a given run of the PVM program. The host pool may be altered by adding and deleting machines at any time (an important feature for fault tolerance). When PVM is used on Beowulf clusters, the nodes within a cluster and/or nodes spanning multiple clusters make up the host pool. There is no restriction on the number of parallel tasks that can exist in a given virtual machine. If the number of tasks exceeds the number of processors in the cluster, then PVM will run multiple tasks per processor.

  • Translucent access to hardware: Application programs may view the hardware environment as a transparent computing resource or may exploit the capabilities of specific machines in the host pool by positioning certain tasks on the most appropriate computers. On large clusters, for example, I/O nodes may run the monitoring tasks and compute nodes may get the bulk of the computing load.

  • Explicit message-passing: PVM provides basic blocking and nonblocking send, receive, and collective communication operations. For performance, PVM uses the native message-passing facilities on multiprocessors to take advantage of the underlying hardware. For example, on the IBM SP, PVM transparently uses IBM's MPI to move data. On the SGI multiprocessor, PVM uses shared memory to move data. On Linux clusters PVM typically uses a mixture of UDP and TCP/IP to move data.

  • Dynamic program model: The PVM system supports a dynamic programming model where hosts and tasks can come and go at any time. PVM tasks are dynamic. New ones can be spawned and existing ones killed at any time by the application or manually from any host in the virtual machine. The virtual machine monitors its state and automatically adapts to such changes.

  • Dynamic Groups: In some applications it is natural to think of a group of tasks. And there are cases where you would like to identify your tasks by the numbers 0 to (p - 1), where p is the number of tasks. PVM includes the concept of user-named groups. When a task joins a group, it is assigned a unique "instance" number in that group. Instance numbers start at 0 and count up (similar to an MPI "rank"). In keeping with the dynamic programming model in PVM , the group functions are designed to be very general and transparent to the user. For example, any PVM task can join or leave any group at any time without having to inform any other task in the affected groups, groups can overlap, and tasks can broadcast messages to groups of which they are not a member. To use any of the group functions, a program must be linked with 'libgpvm3.a'.

10.2 Writing PVM Applications

The PVM system currently supports many languages. C, C++, and Fortran languages are supported in the standard distribution. Third-party groups have created freely available Java, Perl, Python, S, Matlab, TCL/TK, and IDL interfaces to PVM. All these are downloadable from the PVM Web site ( www.csm.ornl.gov/pvm). PVM is designed so that an application can be composed of tasks written in any mixture of these languages and the tasks will still be able to exchange data and to synchronize with each other.

The general paradigm for application programming with PVM is as follows. You write one or more sequential programs that contain embedded calls to the PVM library. Each program corresponds to a task making up the application. These programs are compiled for each architecture in the host pool, and the resulting object files are placed at a location accessible from machines in the host pool. To execute an application, you typically start one copy of one task (typically the "manager" or "initiating" task) by hand from a machine within the host pool. This process subsequently spawns other PVM tasks, eventually resulting in a collection of active tasks that then compute on the cluster and exchange messages with each other to solve the problem.

The C and C++ language bindings for the PVM user interface library are implemented as functions, following the general conventions used by most C systems. To elaborate, function arguments are a combination of value parameters and pointers as appropriate, and function result values indicate the outcome of the call. In addition, macro definitions are used for system constants, and global variables such as errno and pvm_errno are the mechanism for discriminating between multiple possible outcomes. Application programs written in C and C++ access PVM library functions by linking against an archival library ('libpvm3.a') that is part of the standard distribution.

Fortran language bindings are implemented as subroutines rather than as functions. This approach was taken because some compilers on the supported architectures would not reliably interface Fortran functions with C functions. One immediate implication of this is that an additional argument is introduced into each PVM library call for status results to be returned to the invoking program. Moreover, library routines for the placement and retrieval of typed data in message buffers are unified, with an additional parameter indicating the datatype. Apart from these differences (and the standard naming prefixes pvm_ for C, and pvmf for Fortran), a one-to-one correspondence exists between the two language bindings. Fortran interfaces to PVM are implemented as library stubs that in turn invoke the corresponding C routines, after casting and/or dereferencing arguments as appropriate. Thus, Fortran applications are required to link against the stubs library ('libfpvm3.a') as well as the C library.

All PVM tasks are identified by an integer task identifier tid. Messages are sent to tids and received from tids. Since tids must be unique across the entire virtual machine, they are supplied by the local pvmd and are not user chosen. Although PVM encodes information into each tid to improve performance, the user is expected to treat the tids as opaque integer identifiers. PVM contains several routines that return tid values so that the user application can identify other tasks in the system.

As mentioned earlier, tasks interact through explicit message passing, identifying each other with a system-assigned, opaque tid.

Shown in Figure 10.2 is the body of the PVM program 'hello.c', a simple example that illustrates the basic concepts of PVM programming. This program is intended to be invoked manually; after printing its task id (obtained with pvm_mytid()), it initiates a copy of another program called 'hello_other.c' using the pvm_spawn() function. A successful spawn causes the program to execute a blocking receive using pvm_recv. After the message is received, it is unpacked into a format the receiving computer understands using pvm_upkstr. Then the program prints the message as well its task id. The final pvm_exit call dissociates the program from the PVM system.

Start Figure 
 #include "pvm3.h"
 
 main()
 {
         int cc, tid, msgtag;
         char buf [100];
 
         printf("i'm t%x\n", pvm_mytid());
 
         cc = pvm_spawn("hello_other", (char**)0, 0, "", 1, &tid);
 
         if (cc == 1) {
                 msgtag = 1;
                 pvm_recv(tid, msgtag);
                 pvm_upkstr(buf);
                 printf("from t%x: %s\n", tid, buf);
         } else
                 printf("can't start hello_other\n");
 
         pvm_exit();
 }
End Figure

Figure 10.2: PVM program 'hello.c'.

Figure 10.3 is a listing of the hello_other program. Its first PVM action is to obtain the task id of its parent using the pvm_parent call. This program then obtains its hostname and transmits it to the parent using the three-call sequence: pvm_initsend to initialize the (transparent) send buffer; pvm_pkstr to place a string in a strongly typed and architecture-independent manner into the send buffer; and pvm_send to transmit it to the destination process specified by ptid, "tagging" the message with the number 1.

Start Figure 
 #include  "pvm3.h"
 
 main()
 {
         int ptid, msgtag;
         char buf[100];
 
         ptid = pvm_parent();
 
         strcpy(buf, "hello, world from  ");
         gethostname(buf + strlen(buf), 64);
         msgtag = 1;
         pvm_initsend(PvmDataDefault);
         pvm_pkstr(buf);
         pvm_send(ptid, msgtag);
 
         pvm_exit();
 }
End Figure

Figure 10.3: PVM program 'hello_other.c'.

Message tags are user-defined identifiers put on a message by the sender so that the receiving task can selectively get a particular message from the many that may have arrived. The receiver does not have to, nor may it be able to, know the tag put on a message. It is possible in PVM to probe for what tags have arrived so far. It is also possible to ignore the tag and simply receive the messages in the order they arrive at the receiving task. Message tags will become necessary as we explore more complicated PVM examples.

The next example, 'forkjoin.c', demonstrates spawning a parallel application from one cluster node. We then show PVM used in a Fortran dot product program PSDOT.F and a matrix multiply example that demonstrates the use of groups. Lastly, we show an example of a master/worker PVM application that calculates heat diffusion through a wire.

10.2.1 fork/join

The fork/join example demonstrates how to spawn off PVM tasks and synchronize with them. The program spawns the number of tasks specified by the user during startup. The children then synchronize by sending a message to their parent task. The parent receives a message from each of the spawned tasks and prints out information about the message from the child tasks.

This program contains the code for both the parent and the child tasks. Let's examine it in more detail. The first action the program takes is to call pvm_mytid(). In fork/join we check the value of mytid; if it is negative, indicating an error, we call pvm_perror() and exit the program. The pvm_perror() call will print a message indicating what went wrong with the last PVM call. In this case the last call was pvm_mytid(), so pvm_perror() might print a message indicating that PVM hasn't been started on this machine. The argument to pvm_perror() is a string that will be prepended to any error message printed by pvm_perror(). In this case we pass argv[0], which is the name of the program as it was typed on the command-line. The pvm_perror() function is modeled after the Unix perror() function.

Assuming we obtained a valid result for mytid, we now call pvm_parent(). The pvm_parent() function will return the tid of the task that spawned the calling task. Since we run the initial forkjoin program from a command prompt, this initial task will not have a parent; it will not have been spawned by some other PVM task but will have been started manually by the user. For the initial fork/join task the result of pvm_parent() will not be any particular task id but an error code, PvmNoParent. Thus we can distinguish the parent fork/join task from the children by checking whether the result of the pvm_parent() call is equal to PvmNoParent. If this task is the parent, then it must spawn the children. If it is not the parent, then it must send a message to the parent.

Let's examine the code executed by the parent task. The number of tasks is taken from the command-line as argv[1]. If the number of tasks is not legal, then we exit the program, calling pvm_exit() and then returning. The call to pvm_exit() is important because it tells PVM this program will no longer be using any of the PVM facilities. (In this case the task exits and PVM will deduce that the dead task no longer needs its services. Regardless, it is good style to exit cleanly.) If the number of tasks is valid, fork/join will then attempt to spawn the children.

The pvm_spawn() call tells PVM to start ntask tasks named argv[0]. The second parameter is the argument list given to the spawned tasks. In this case we don't care to give the children any particular command-line arguments, so this value is null. The third parameter to spawn, PvmTaskDefault, is a flag telling PVM to spawn the tasks in the default method. The default method is to distribute the tasks round robin to all the cluster nodes in the virtual machine. Had we been interested in placing the children on a specific machine or a machine of a particular architecture, we would have used PvmTaskHost or PvmTaskArch for this flag and specified the host or architecture as the fourth parameter. Since we don't care where the tasks execute, we use PvmTaskDefault for the flag and null for the fourth parameter. Finally, ntask tells spawn how many tasks to start, and the integer array child will hold the task ids of the newly spawned children. The return value of pvm_spawn() indicates how many tasks were successfully spawned. If info is not equal to ntask, then some error occurred during the spawn. In case of an error, the error code is placed in the task id array, child, instead of the actual task id; forkjoin loops over this array and prints the task ids or any error codes. If no tasks were successfully spawned, then the program exits.

For each child task, the parent receives a message and prints out information about that message. The pvm_recv() call receives a message from any task as long as the tag for that message is JOINTAG. The return value of pvm_recv() is an integer indicating a message buffer. This integer can be used to find out information about message buffers. The subsequent call to pvm_bufinfo() does just this; it gets the length, tag, and task id of the sending process for the message indicated by buf. In forkjoin the messages sent by the children contain a single integer value, the task id of the child task. The pvm_upkint() call unpacks the integer from the message into the mydata variable. As a sanity check, forkjoin tests the value of mydata and the task id returned by pvm_bufinfo(). If the values differ, the program has a bug, and an error message is printed. Finally, the information about the message is printed, and the parent program exits.

The last segment of code in forkjoin will be executed by the child tasks. Before data is placed in a message buffer, the buffer must be initialized by calling pvm_initsend(). The parameter PvmDataDefault indicates that PVM should do whatever data conversion is needed to ensure that the data arrives in the correct format on the destination processor. In some cases this may result in unnecessary data conversions. If you are sure no data conversion will be needed because the destination machine uses the same data format, then you can use PvmDataRaw as a parameter to pvm_initsend(). The pvm_pkint() call places a single integer, mytid, into the message buffer. It is important to make sure the corresponding unpack call exactly matches the pack call. Packing an integer and unpacking it as a float is an error. There should be a one-to-one correspondence between pack and unpack calls. Finally, the message is sent to the parent task using a message tag of JOINTAG.

       pvm_perror("calling pvm_initsend"); pvm_exit(); return -1;
       }
    info = pvm_pkint(&mytid, 1, 1);
    if (info < 0) {
       pvm_perror("calling pvm_pkint"); pvm_exit(); return -1;
       }
    info = pvm_send(myparent, JOINTAG);
    if (info < 0) {
       pvm_perror("calling pvm_send"); pvm_exit(); return -1;
       }
    pvm_exit();
    return 0;
 }

Figure 10.4 shows the output of running fork/join. Notice that the order the messages were received is nondeterministic. Since the main loop of the parent processes messages on a first-come first-served basis, the order of the prints are determined simply by the time it takes messages to travel from the child tasks to the parent.

Start Figure 
 /*
     Fork Join Example
     Demonstrates how to spawn processes and exchange messages
 */
     /* defines and prototypes for the PVM library */
     #include <pvm3.h>
 
     /* Maximum number of children this program will spawn */
     #define MAXNCHILD  20
     /* Tag to use for the joing message */
     #define JOINTAG    11
 
     int
     main(int argc, char* argv[])
     {
 
         /* number of tasks to spawn, use 3 as the default */
         int ntask = 3;
         /* return code from pvm calls */
         int info;
         /* my task id */
         int mytid;
         /* my parents task id */
         int myparent;
         /* children task id array */
         int child[MAXNCHILD];
         int i, mydata, buf, len, tag, tid;
 
         /* find out my task id number */
         mytid = pvm_mytid();
 
         /* check for error */
         if (mytid < 0) {
             /* print out the error */
             pvm_perror(argv[0]);
             /* exit the program */
             return -1;
             }
         /* find my parent's task id number */
         myparent = pvm_parent();
 
         /* exit if there is some error other than PvmNoParent */
         if ((myparent < 0) && (myparent != PvmNoParent)
              && (myparent != PvmParentNotSet)) {
             pvm_perror(argv[0]);
             pvm_exit ();
             return -1;
             }
     /* if i don't have a parent then i am the parent */
     if (myparent == PvmNoParent || myparent == PvmParentNotSet) {
         /*  find out how many tasks to spawn */
         if (argc == 2) ntask = atoi(argv[l]) ;
 
         /* make sure ntask is legal */
         if ((ntask < 1) || (ntask > MAXNCHILD)) { pvm_exit(); return 0; }
 
         /* spawn the child tasks */
         info = pvm_spawn(argv[0], (char**)0, PvmTaskDefault, (char*)0,
             ntask, child);
         /* print out the task ids */
         for (i = 0; i < ntask; i++)
             if (child[i] < 0) /* print the error code in decimal*/
                 printf(" %d", child[i]);
             else /* print the task id in hex */
                 printf("t%x\t", child[i]);
         putchar('\n');
 
         /* make sure spawn succeeded */
         if (info == 0) { pvm_exit(); return -1; }
 
         /* only expect responses from those spawned correctly */
         ntask = info;
 
         for (i = 0; i < ntask; i++) {
             /* recv a message from any child process */
             buf = pvm_recv(-1, JOINTAG);
             if (buf < 0) pvm_perror("calling recv");
             info = pvm_bufinfo(buf, &len, &tag, &tid);
             if (info < 0) pvm_perror("calling pvm_bufinfo");
             info = pvm_upkint(&mydata, 1, 1);
             if (info < 0) pvm_perror("calling pvm_upkint");
             if (mydata != tid) printf("This should not happen!\n");
             printf("Length %d, Tag %d, Tid t%x\n", len, tag, tid);
             }
         pvm_exit();
         return 0;
         }
 
     /* i'm a child */
     info = pvm_initsend(PvmDataDefault);
     if (info < 0) {
         % forkjoin
         t10001c t40149  tc0037
         Length 4, Tag 11, Tid t40149
         Length 4, Tag 11, Tid tc0037
         Length 4, Tag 11, Tid t10001c
         % forkjoin 4
         t10001e t10001d t4014b  tc0038
         Length 4, Tag 11, Tid t4014b
         Length 4, Tag 11, Tid tc0038
         Length 4, Tag 11, Tid t10001d
         Length 4, Tag 11, Tid t10001e
End Figure

Figure 10.4: Output of fork/join program.

10.2.2 Dot Product

Here we show a simple Fortran program, PSDOT, for computing a dot product. The program computes the dot product of two arrays, X and Y. First PSDOT calls PVMFMYTID() and PVMFPARENT(). The PVMFPARENT call will return PVMNOPARENT if the task wasn't spawned by another PVM task. If this is the case, then PSDOT task is the master and must spawn the other worker copies of PSDOT.PSDOT then asks the user for the number of processes to use and the length of vectors to compute. Each spawned process will receive n/nproc elements of X and Y, where n is the length of the vectors and nproc is the number of processes being used in the computation. If nproc does not divide n evenly, then the master will compute the dot product on the extra elements. The subroutine SGENMAT randomly generates values for X and Y. PSDOT then spawns nproc-1 copies of itself and sends each new task a part of the X and Y arrays. The message contains the length of the subarrays in the message and the subarrays themselves. After the master spawns the worker processes and sends out the subvectors, the master then computes the dot product on its portion of X and Y. The master process then receives the other local dot products from the worker processes. Notice that the PVMFRECV call uses a wild card (-1) for the task id parameter. This indicates that a message from any task will satisfy the receive. Using the wild card in this manner results in a race condition. In this case the race condition does not cause a problem because addition is commutative; in other words, it doesn't matter in which order we add up the partial sums from the workers. However, unless one is certain that the race will not affect the program adversely, race conditions should be avoided.

Once the master receives all the local dot products and sums them into a global dot product, it then calculates the entire dot product locally. These two results are then subtracted, and the difference between the two values is printed. A small difference can be expected because of the variation in floating-point roundoff errors.

If the PSDOT program is a worker, then it receives a message from the master process containing subarrays of X and Y. It calculates the dot product of these subarrays and sends the result back to the master process. In the interests of brevity we do not include the SGENMAT and SDOT subroutines.

      PROGRAM PSDOT
 *
 * PSDOT performs a parallel inner (or dot) product, where the vectors
 * X and Y start out on a master node, which then sets up the virtual
 * machine, farms out the data and work, and sums up the local pieces
 * to get a global inner product.
 *
 *    .. External Subroutines ..
      EXTERNAL PVMFMYTID, PVMFPARENT, PVMFSPAWN, PVMFEXIT, PVMFINITSEND
      EXTERNAL PVMFPACK, PVMFSEND, PVMFRECV, PVMFUNPACK, SGENMAT
 *
 *    .. External Functions ..
      INTEGER ISAMAX
      REAL SDOT
      EXTERNAL ISAMAX, SDOT
 *
 *    .. Intrinsic Functions ..
      INTRINSIC MOD
 *
 *    .. Parameters ..
      INTEGER MAXN
      PARAMETER ( MAXN = 8000 )
      INCLUDE 'fpvm3.h'
 *
 *    .. Scalars ..
      INTEGER N, LN, MYTID, NPROCS, IBUF, IERR
      INTEGER I, J, K
      REAL LOOT, GDOT
 *
 *    .. Arrays ..
      INTEGER TIDS(0:63)
      REAL X(MAXN), Y(MAXN)
 *
 *    Enroll in PVM and get my and the master process' task ID number
 *
      CALL PVMFMYTID( MYTID )
      CALL PVMFPARENT( TIDS(0) )
 *
 *    If I need to spawn other processes (I am master process)
 *
      IF ( TIDS(0) EQ. PVMNOPARENT ) THEN
 *
 *       Get starting information
 *
         WRITE(*,*) 'How many processes should participate (1-64)?'
         READ(*,*) NPROCS
         WRITE(*,2000) MAXN
         READ(*,*) N
         TIDS(0) = MYTID
         IF ( N GT. MAXN ) THEN
            WRITE(*,*) 'N too large.  Increase parameter MAXN to run'//
      $                'this case.'
            STOP
         END IF
 *
 *       LN is the number of elements of the dot product to do
 *       locally.  Everyone has the same number, with the master
 *       getting any left over elements.  J stores the number of
 *       elements rest of procs do.
 *
         J = N / NPROCS
         LN = J + MOD(N, NPROCS)
         I = LN + 1
 *
 *       Randomly generate X and Y
 *       Note: SGENMAT() routine is not provided here
 *
         CALL SGENMAT( N, 1, X, N, MYTID, NPROCS, MAXN, J )
         CALL SGENMAT( N, 1, Y, N, I, N, LN, NPROCS )
 *
 *       Loop over all worker processes
 *
         DO 10 K = 1, NPROCS-1
 *
 *          Spawn process and check for error
 *
            CALL PVMFSPAWN( 'psdot', 0, 'anywhere', 1, TIDS(K), IERR )
            IF (IERR .NE. 1) THEN
               WRITE(*,*) 'ERROR, could not spawn process #',K,
      $                   '. Dying . . .'
               CALL PVMFEXIT( IERR )
               STOP
            END IF
 *
 *          Send out startup info
 *
            CALL PVMFINITSEND( PVMDEFAULT, IBUF )
            CALL PVMFPACK( INTEGER4, J, 1, 1, IERR )
            CALL PVMFPACK( REAL4, X(I), J, 1, IERR )
            CALL PVMFPACK( REAL4, Y(I), J, 1, IERR )
            CALL PVMFSEND( TIDS(K), 0, IERR )
            I = I + J
    10   CONTINUE
 *
 *       Figure master's part of dot product
 *       SDOT() is part of the BLAS Library (compile with -lblas)
 *
         GDOT = SDOT( LN, X, 1, Y, 1 )
 *
 *       Receive the local dot products, and
 *       add to get the global dot product
 *
         DO 20 K = 1, NPROCS-1
            CALL PVMFRECV( -1, 1, IBUF )
            CALL PVMFUNPACK( REAL4, LDOT, 1, 1, IERR )
            GDOT = GDOT + LDOT
    20   CONTINUE
 *
 *       Print out result
 *
         WRITE(*,*) ' '
         WRITE(*,*) '<x,y> = ',GDOT
 *
 *       Do sequential dot product and subtract from
 *       distributed dot product to get desired error estimate
 *
         LDOT = SDOT( N, X, 1, Y, 1 )
         WRITE(*,*) '<x,y> : sequential dot product.  <x,y>^ : '//
     $              'distributed dot product.'
         WRITE(*,*) '| <x,y> - <x,y>^ | = ' ,ABS(GDOT - LDOT)
         WRITE(*,*) 'Run completed.'
 *
 *    If I am a worker process (i.e. spawned by master process)
 *
      ELSE
 *
 *       Receive startup info
 *
         CALL PVMFRECV( TIDS(0), 0, IBUF )
         CALL PVMFUNPACK( INTEGER4, LN, 1, 1, IERR )
         CALL PVMFUNPACK( REAL4, X, LN, 1, IERR )
         CALL PVMFUNPACK( REAL4, Y, LN, 1, IERR )
 *
 *       Figure local dot product and send it in to master
 *
         LDOT = SDOT( LN, X, 1, Y, 1 )
         CALL PVMFINITSEND( PVMDEFAULT, IBUF )
         CALL PVMFPACK( REAL4, LDOT, 1, 1, IERR )
         CALL PVMFSEND( TIDS(0), 1, IERR )
     END IF
 *
      CALL PVMFEXIT( 0 )
 *
 1000 FORMAT(I10,' Successfully spawned process #' ,I2,', TID =',I10)
 2000 FORMAT('Enter the length of vectors to multiply (1 -',I7,'):')
      STOP
 *
 *    End program PSDOT
 *
      END

10.2.3 Matrix Multiply

In this example we program a matrix multiply algorithm described by Fox et al. in [39]. The mmult program can be found at the end of this section. The mmult program will calculate C = AB where C, A, and B are all square matrices. For simplicity we assume that m ?m tasks are used to calculate the solution. Each task calculates a subblock of the resulting matrix C. The block size and the value of m are given as a command-line argument to the program. The matrices A and B are also stored as blocks distributed over the m2 tasks. Before delving into the details of the program, let us first describe the algorithm at a high level.

In our grid of m x m tasks, each task (tij, where 0 ≤ i, j < m), initially contains blocks Cij, Aij, and Bij. In the first step of the algorithm the tasks on the diagonal (tij where i = j) send their block Aii to all the other tasks in row i. After the transmission of Aii, all tasks calculate Aii ?Bij and add the result into Cij. In the next step, the column blocks of B are rotated. That is, tij sends its block of B to t(i-1)j. (Task t0j sends its B block to t(m-1)j.) The tasks now return to the first step, Ai(i+1) is multicast to all other tasks in row i, and the algorithm continues. After m iterations, the C matrix contains A ?B, and the B matrix has been rotated back into place.

Let us now go over the matrix multiply as it is programmed in PVM. In PVM there is no restriction on which tasks may communicate with which other tasks. However, for this program we would like to think of the tasks as a two-dimensional conceptual torus. In order to enumerate the tasks, each task joins the group mmult. Group ids are used to map tasks to our torus. The first task to join a group is given the group id of zero. In the mmult program, the task with group id zero spawns the other tasks and sends the parameters for the matrix multiply to those tasks. The parameters are m and bklsize, the square root of the number of blocks and the size of a block, respectively. After all the tasks have been spawned and the parameters transmitted, pvm_barrier() is called to make sure all the tasks have joined the group. If the barrier is not performed, later calls to pvm_gettid() might fail because a task may not have yet joined the group.

After the barrier, the task ids for the other tasks are stored in the row in the array myrow. Specifically, the program calculates group ids for all the tasks in the row, and we ask PVM for the task id for the corresponding group id. Next the program allocates the blocks for the matrices using malloc(). (In an actual application program we would expect that the matrices would already be allocated.) Then the program calculates the row and column of the block of C it will be computing; this calculation is based on the value of the group id. The group ids range from 0 to m - 1 inclusive. Thus, the integer division of (mygid/m) will give the task's row and (mygid mod m) will give the column if we assume a row major mapping of group ids to tasks. Using a similar mapping, we calculate the group id of the task directly above and below in the torus and store their task ids in up and down, respectively.

Next the blocks are initialized by calling InitBlock(). This function simply initializes A to random values, B to the identity matrix, and C to zeros. This will allow us to verify the computation at the end of the program by checking that A = C.

Finally we enter the main loop to calculate the matrix multiply. First the tasks on the diagonal multicast their block of A to the other tasks in their row. Note that the array myrow actually contains the task id of the task doing the multicast. Recall that pvm_mcast() will send to all the tasks in the tasks array except the calling task. This approach works well in the case of mmult because we don't want to have to needlessly handle the extra message coming into the multicasting task with an extra pvm_recv(). Both the multicasting task and the tasks receiving the block calculate the AB for the diagonal block and the block of B residing in the task.

After the subblocks have been multiplied and added into the C block, we now shift the B blocks vertically. Specifically, the block of B is packed into a message and sent to the up task id; then a new B block is received from the down task id.

Note that we use different message tags for sending the A blocks and the B blocks as well as for different iterations of the loop. We also fully specify the task ids when doing a pvm_recv(). It's tempting to use wild cards for the fields of pvm_recv(); however, such use can be dangerous. For instance, had we incorrectly calculated the value for up and used a wild card for the pvm_recv() instead of down, we would be sending messages to the wrong tasks without knowing it. In this example we fully specify messages, thereby reducing the possibility of receiving a message from the wrong task or the wrong phase of the algorithm.

Once the computation is complete, we check to see that A = C, just to verify that the matrix multiply correctly calculated the values of C. This step would not be done in a matrix-multiply library routine, for example.

You do not have to call pvm_lvgroup() because PVM will automatically detect that the task has exited and will remove it from the group. It is good form, however, to leave the group before calling pvm_exit(). The reset command from the PVM console will reset all the PVM groups. The pvm_gstat command will print the status of any groups that currently exist.

 /*
     Matrix Multiply
 */
 
 /* defines and prototypes for the PVM library */
 #include <pvm3.h>
 #include <stdio.h>
 
 /* Maximum number of children this program will spawn */
 #define MAXNTIDS    100
 #define MAXROW      10
 
 /* Message tags */
 #define ATAG        2
 #define BTAG        3
 #define DIMTAG      5
 
 void
 InitBlock(float *a, float *b, float *c, int blk, int row, int col)
 {
     int len, ind;
     int i,j;
 
     srand(pvm_mytid());
     len = blk*blk;
     for (ind = 0; ind < len; ind++)
         { a[ind] = (float)(rand()%1000)/100.0; c[ind] = 0.0; }
     for (i = 0; i < blk; i++) {
         for (j = 0; j < blk; j++) {
             if (row == col)
                 b[j*blk+i] = (i==j)? 1.0 : 0.0;
             else
                 b[j*blk+i] = 0.0;
             }
         }
 }
 
 void
 BlockMult(float* c, float* a, float* b, int blk)
 {
     int i,j,k;
     for (i = 0; i < blk; i++)
         for (j = 0; j < blk; j ++)
             for (k = 0; k < blk; k++)
                 c[i*blk+j] += (a[i*blk+k] * b[k*blk+j]);
 }
 
 int
 main(int argc, char* argv[])
 {
 
     /* number of tasks to spawn, use 3 as the default */
     int ntask = 2;
     /* return code from pvm calls */
     int info;
     /* my task and group id */
     int mytid, mygid;
     /* children task id array */
     int child[MAXNTIDS-1];
     int i, m, blksize;
     /* array of the tids in my row */
     int myrow[MAXROW];
     float *a, *b, *c, *atmp;
     int row, col, up, down;
 
     /* find out my task id number */
     mytid = pvm_mytid();
     pvm_setopt(PvmRoute, PvmRouteDirect);
 
     /* check for error */
     if (mytid < 0) {
         /* print out the error */
         pvm_perror(argv[0]);
         /* exit the program */
         return -1;
         }
 
     /* join the mmult group */
     mygid = pvm_joingroup("mmult");
     if (mygid < 0) {
         pvm_perror(argv[0]); pvm_exit(); return -1;
         }
 
     /* if my group id is 0 then I must spawn the other tasks */
 if (mygid == 0) {
     /* find out how many tasks to spawn */
     if (argc == 3) {
         m = atoi(argv[1]);
         blksize = atoi(argv[2]);
         }
     if (argc < 3) {
         fprintf(stderr, "usage: mmult m blk\n");
         pvm_lvgroup("mmult"); pvm_exit(); return -1;
         }
 
     /* make sure ntask is legal */
     ntask = m*m;
     if ((ntask < 1) || (ntask >= MAXNTIDS)) {
         fprintf(stderr, "ntask = %d not valid.\n", ntask);
         pvm_lvgroup("mmult"); pvm_exit(); return -1;
         }
     /* if there is more than one task spawn them*/
     if (ntask > 1) {
 
         /* spawn the child tasks */
         info = pvm_spawn("mmult", (char**)0, PvmTaskDefault, (char*)0,
         ntask-1, child);
 
         /* make sure spawn succeeded */
         if (info != ntask-1) {
             pvm_lvgroup("mmult"); pvm_exit(); return -1;
             }
 
         /* send the matrix dimension */
         pvm_initsend(PvmDataDefault);
         pvm_pkint(&m, 1, 1);
         pvm_pkint(&blksize, 1, 1);
         pvm_mcast(child, ntask-1, DIMTAG);
         }
     }
 else {
     /* recv the matrix dimension */
     pvm_recv(pvm_gettid("mmult", 0), DIMTAG);
     pvm_upkint(&m, 1, 1);
     pvm_upkint(&blksize, 1, 1);
     ntask = m*m;
     }
 /* make sure all tasks have joined the group */
 
 info = pvm_barrier("mmult",ntask);
 if (info < 0) pvm_perror(argv[0]);
 
 /* find the tids in my row */
 for (i = 0; i < m; i++)
     myrow[i] = pvm_gettid("mmult", (mygid/m)*m + i);
 
 /* allocate the memory for the local blocks */
 a = (float*)malloc(sizeof(float)*blksize*blksize);
 b = (float*)malloc(sizeof(float)*blksize*blksize);
 c = (float*)malloc(sizeof(float)*blksize*blksize);
 atmp = (float*)malloc(sizeof(float)*blksize*blksize);
 /* check for valid pointers */
 if (!(a && b && c && atmp)) {
     fprintf(stderr, "%s: out of memory!\n", argv[0]);
     free(a); free(b); free(c); free(atmp);
     pvm_lvgroup("mmult"); pvm_exit(); return -1;
     }
 
 /* find my block's row and column */
 row = mygid/m; col = mygid % m;
 /* calculate the neighbor's above and below */
 up = pvm_gettid("mmult", ((row)?(row-1):(m-1))*m+col);
 down = pvm_gettid("mmult", ((row == (m-1))?col:(row+1)*m+col));
 
 /* initialize the blocks */
 InitBlock(a, b, c, blksize, row, col);
 
 /* do the matrix multiply */
 for (i = 0; i < m; i++) {
     /* mcast the block of matrix A */
     if (col == (row + i)%m) {
         pvm_initsend(PvmDataDefault);
         pvm_pkfloat(a, blksize*blksize, 1);
         pvm_mcast(myrow, m, (i+1)*ATAG);
         BlockMult(c,a,b,blksize);
         }
     else {
         pvm_recv(pvm_gettid("mmult", row*m + (row +i)%m), (i+1)*ATAG);
         pvm_upkfloat(atmp, blksize*blksize, 1);
         BlockMult(c,atmp,b,blksize);
         }
         /* rotate the columns of B */
         pvm_initsend(PvmDataDefault);
         pvm_pkfloat(b, blksize*blksize, 1);
         pvm_send(up, (i+1)*BTAG);
         pvm_recv(down, (i+1)*BTAG);
         pvm_upkfloat(b, blksize*blksize, 1);
         }
 
     /* check it */
     for (i = 0 ; i < blksize*blksize; i++)
         if (a[i] != c[i])
             printf("Error a[%d] (%g) != c[%d] (%g) \n", i, a[i],i,c[i]);
 
     printf("Done.\n");
     free(a); free(b); free(c); free(atmp);
     pvm_lvgroup("mmult");
     pvm_exit();
     return 0;
 }

10.2.4 One-Dimensional Heat Equation

Here we present a PVM program that calculates heat diffusion through a substrate, in this case a wire. Consider the one-dimensional heat equation on a thin wire,

(10.1)

and a discretization of the form

(10.2)

giving the explicit formula

(10.3)

The initial and boundary conditions are

A(t, 0) = 0, A(t, 1) = 0 for all t

A(0, x) = sin(πx) for 0 ≤ x ≤ 1.

The pseudocode for this computation is as follows:

     for i = 1:tsteps-1;
         t = t+dt;
         a(i+1,1)=0;
         a(i+1,n+2)=0;
         for j = 2:n+1;
             a(i+1,j)=a(i,j) + mu*(a(i,j+1)-2*a(i,j)+a(i,j-1));
         end;
     end

For this example we use a master/worker programming model. The master, 'heat.c', spawns five copies of the program heatslv. The workers compute the heat diffusion for subsections of the wire in parallel. At each time step the workers exchange boundary information, in this case the temperature of the wire at the boundaries between processors.

Let's take a closer look at the code. In 'heat.c' the array solution will hold the solution for the heat diffusion equation at each time step. First the heatslv tasks are spawned. Next, the initial dataset is computed. Notice that the ends of the wires are given initial temperature values of zero.

The main part of the program is then executed four times, each with a different value for Δt. A timer is used to compute the elapsed time of each compute phase. The initial datasets are sent to the heatslv tasks. The left and right neighbor task ids are sent along with the initial dataset. The heatslv tasks use these to communicate boundary information. Alternatively, we could have used the PVM group calls to map tasks to segments of the wire. By using that approach we would have avoided explicitly communicating the task ids to the slave processes.

After sending the initial data, the master process waits for results. When the results arrive, they are integrated into the solution matrix, the elapsed time is calculated, and the solution is written to the output file.

Once the data for all four phases have been computed and stored, the master program prints out the elapsed times and kills the slave processes.

 /*
 heat.c
 
     Use PVM to solve a simple heat diffusion differential equation,
     using 1 master program and 5 slaves.
 
     The master program sets up the data, communicates it to the slaves
     and waits for the results to be sent from the slaves.
     Produces xgraph ready files of the results.
 */
 
 #include "pvm3.h"
 #include <stdio.h>
 #include <math.h>
 #include <time.h>
 #define SLAVENAME "heatslv"
 #define NPROC 5
 #define TIMESTEP 100
 #define PLOTINC 10
 #define SIZE 1000
 
 int num_data = SIZE/NPROC;
 
 main()
 {   int mytid, task_ids[NPROC], i, j;
     int left, right, k, 1;
     int step = TIMESTEP;
     int info;
 
     double init[SIZE], solution[TIMESTEP][SIZE];
     double result[TIMESTEP*SIZE/NPROC], deltax2;
     FILE *filenum;
     char *filename [4] [7] ;
     double deltat[4];
     time_t t0;
     int etime [4] ;
 
     filename[0][0] = "graph1";
     filename[1][0] = "graph2";
     filename[2][0] = "graph3";
     filename[3][0] = "graph4";
 
     deltat[0] = 5.0e-1;
     deltat[1] = 5.0e-3;
     deltat[2] = 5.0e-6;
     deltat[3] = 5.0e-9;
 
 /* enroll in pvm */
     mytid = pvm_mytid();
 
 /* spawn the slave tasks */
     info = pvm_spawn(SLAVENAME,(char **)0,PvmTaskDefault,"",
         NPROC,task_ids);
 /* create the initial data set */
     for (i = 0; i < SIZE; i++)
         init[i] = sin(M_PI * ( (double)i / (double)(SIZE-1) ));
     init[0] = 0.0;
     init[SIZE-1] = 0.0;
 
 /* run the problem 4 times for different values of delta t */
     for (1 = 0; 1 < 4; 1++) {
         deltax2 = (deltat[1]/pow(1.0/(double)SIZE,2.0));
         /* start timing for this run */
         time(&t0);
         etime[1] = t0;
 /* send the initial data to the slaves. */
 /* include neighbor info for exchanging boundary data */
     for (i = 0; i < NPROC; i++) {
         pvm_initsend(PvmDataDefault);
         left = (i == 0) ? 0 : task_ids[i-1];
         pvm_pkint(&left, 1, 1);
         right = (i == (NPROC-1)) ? 0 : task_ids[i+1];
         pvm_pkint(&right, 1, 1);
         pvm_pkint(&step, 1, 1);
         pvm_pkdouble(&deltax2, 1, 1);
         pvm_pkint(&num_data, 1, 1);
         pvm_pkdouble(&init[num_data*i], num_data, 1);
         pvm_send(task_ids[i], 4);
         }
 
 /* wait for the results */
         for (i = 0; i < NPROC; i++) {
             pvm_recv(task_ids[i], 7);
             pvm_upkdouble(&result[0], num_data*TIMESTEP, 1);
 /* update the solution */
         for (j = 0; j < TIMESTEP; j++)
             for (k = 0; k < num_data; k++)
                 solution[j][num_data*i+k] = result[wh(j,k)];
         }
 
 /* stop timing */
         time(&t0);
         etime[1] = t0 - etime[l];
 
 /* produce the output */
         filenum = fopen(filename[1][0], "w");
         fprintf(filenum,"TitleText: Wire Heat over Delta Time: %e\n",
             deltat[1]);
         fprintf(filenum,"XUnitText: Distance\nYUnitText: Heat\n");
         for (i = 0; i < TIMESTEP; i = i + PLOTINC) {
             fprintf(filenum,"\"Time index: %d\n",i);
             for (j = 0; j < SIZE; j++)
                 fprintf(filenum,"%d %e\n",j, solution[i][j]);
             fprintf(filenum,"\n");
             }
         fclose (filenum);
     }
 
 /* print the timing information */
     printf("Problem size: %d\n",SIZE);
     for (i = 0; i < 4; i++)
         printf("Time for run %d: %d sec\n",i,etime[i]);
 
 /* kill the slave processes */
     for (i = 0; i < NPROC; i++) pvm_kill(task_ids[i]);
     pvm_exit();
 }
 
 int wh(x, y)
 int x, y;
 {
     return(x*num_data+y);
 }

The heatslv programs do the actual computation of the heat diffusion through the wire. The worker program consists of an infinite loop that receives an initial dataset, iteratively computes a solution based on this dataset (exchanging boundary information with neighbors on each iteration), and sends the resulting partial solution back to the master process. As an alternative to using an infinite loop in the worker tasks, we could send a special message to the worker ordering it to exit. Instead, we simply use the infinite loop in the worker tasks and kill them off from the master program. A third option would be to have the workers execute only once, exiting after processing a single dataset from the master. This would require placing the master's spawn call inside the main for loop of 'heat.c'. While this option would work, it would needlessly add overhead to the overall computation.

For each time step and before each compute phase, the boundary values of the temperature matrix are exchanged. The left-hand boundary elements are first sent to the left neighbor task and received from the right neighbor task. Symmetrically, the right-hand boundary elements are sent to the right neighbor and then received from the left neighbor. The task ids for the neighbors are checked to make sure no attempt is made to send or receive messages to nonexistent tasks.

 /*
 
 heatslv.c
 
     The slaves receive the initial data from the host,
     exchange boundary information with neighbors,
     and calculate the heat change in the wire.
     This is done for a number of iterations, sent by the master.
 
 */
 
 #include "pvm3.h"
 #include <stdio.h>
 
 int num_data;
 
 main()
 {
     int mytid, left, right, i, j, master;
     int timestep;
 
     double *init, *A;
     double leftdata, rightdata, delta, leftside, rightside;
 
 /* enroll in pvm */
     mytid = pvm_mytid();
     master = pvm_parent();
 
 /* receive my data from the master program */
   while(1) {
     pvm_recv(master, 4);
     pvm_upkint(&left, 1, 1);
     pvm_upkint(&right, 1, 1);
     pvm_upkint(&timestep, 1, 1);
     pvm_upkdouble(&delta, 1, 1);
     pvm_upkint(&num_data, 1, 1);
     init = (double *) malloc(num_data*sizeof(double));
     pvm_upkdouble(init, num_data, 1);
 
 /* copy the initial data into my working array */
     A = (double *) malloc(num_data * timestep * sizeof(double));
     for (i = 0; i < num_data; i++) A[i] = init[i];
 
 /* perform the calculation */
 
   for (i = 0; i < timestep-1; i++) {
     /* trade boundary info with my neighbors */
     /* send left, receive right */
     if (left != 0) {
         pvm_initsend(PvmDataDefault);
         pvm_pkdouble(&A[wh(i,0)],1,1);
         pvm_send(left, 5);
         }
     if (right != 0) {
         pvm_recv(right, 5);
         pvm_upkdouble(&rightdata, 1, 1);
     /* send right, receive left */
         pvm_initsend(PvmDataDefault);
         pvm_pkdouble(&A[wh(i,num_data-1)],1,1);
         pvm_send(right, 6);
         }
     if (left != 0) {
         pvm_recv(left, 6);
         pvm_upkdouble(&leftdata,1,1);
         }
 
 /* do the calculations for this iteration */
 
     for (j = 0; j < num_data; j++) {
         leftside = (j == 0) ? leftdata : A[wh(i,j-1)];
         rightside = (j == (num_data-1)) ? rightdata : A[wh(i,j+1)];
         if ((j==0)&&(left==0))
             A[wh(i+1,j)] = 0.0;
         else if ((j==(num_data-1))&&(right==0))
             A[wh(i+1,j)] = 0.0;
         else
             A[wh(i+1,j)]=
                 A[wh(i,j)]+delta*(rightside-2*A[wh(i,j)]+leftside);
         }
   }
 
 /* send the results back to the master program */
 
     pvm_initsend(PvmDataDefault);
     pvm_pkdouble(&A[0],num_data*timestep,1);
     pvm_send(master,7);
   }
 
 /* just for good measure */
   pvm_exit();
 }
 
 int wh(x, y)
 int x, y;
 {
     return(x*num_data+y);
 }

In this section we have given a variety of example programs written in both Fortran and C. These examples demonstrate various ways of writing PVM programs. Some divide the application into two separate programs, while others use a single program with conditionals to handle spawning and computing phases. These examples show different styles of communication, both among worker tasks and between worker and master tasks. In some cases messages are used for synchronization, and in others the master processes simply kill off the workers when they are no longer needed.

10.3 Installing PVM

This section describes how to set up the PVM software package, how to configure a simple virtual machine, and how to compile and run the example programs supplied with PVM. The first part describes the straightforward use of PVM and the most common problems in setting up and running PVM. The latter part describes some of the more advanced options available for customizing your PVM environment.

10.3.1 Setting Up PVM

One of the reasons for PVM's popularity is that PVM is simple to set up and use. It does not require special privileges to be installed. Anyone with a valid login on the hosts can do so. In addition, only one person at an organization needs to get and install PVM for everyone at that organization to use it.

PVM uses two environment variables when starting and running. Each PVM user needs to set these two variables to use PVM. The first variable is PVM_ROOT, which is set to the location of the installed pvm3 directory. The second variable is PVM_ARCH, which tells PVM the architecture of this host and thus what executables to pick from the PVM_ROOT directory.

Because of security concerns many sites no longer allow any of their computers, including those in clusters, to use rsh, which is what PVM uses by default to add hosts to a virtual machine. It is easy to configure PVM to use ssh instead. Just edit the file 'PVM_ROOT/conf/PVM_ARCH.def' and replace rsh with ssh then recompile PVM and your applications.

If PVM is already installed at your site, you can skip ahead to " Creating Your Personal PVM." The PVM source comes with directories and makefiles for Linux and most architectures you are likely to have in your cluster. Building for each architecture type is done automatically by logging on to a host, going into the PVM_ROOT directory, and typing make. The 'makefile' will automatically determine which architecture it is being executed on, create appropriate subdirectories, and build pvmd3, libpvm3.a, and libfpvm3.a, pvmgs, and libgpvm3.a. It places all these files in 'PVM_ROOT/lib/PVM_ARCH' with the exception of pvmgs, which is placed in 'PVM_ROOT/bin/PVM_ARCH'.

Setup Summary

  • Set PVM_ROOT and PVM_ARCH in your '.cshrc' file.

  • Build PVM for each architecture type.

  • Create an '.rhosts' file on each host listing all the hosts.

  • Create a '$HOME/.xpvm_hosts' file listing all the hosts prepended by an "&".

10.3.2 Creating Your Personal PVM

Before we go over the steps to compile and run parallel PVM programs, you should be sure you can start up PVM and configure a virtual machine. On any host on which PVM has been installed you can type

 % pvm

and you should get back a PVM console prompt signifying that PVM is now running on this host. You can add hosts to your virtual machine by typing at the console prompt

 pvm> add hostname

You also can delete hosts (except the one you are on) from your virtual machine by typing

 pvm> delete hostname

If you get the message "Can't Start pvmd," PVM will run autodiagnostics and report the reason found.

To see what the present virtual machine looks like, you can type

 pvm> conf

To see what PVM tasks are running on the virtual machine, you can type

 pvm> ps -a

Of course, you don't have any tasks running yet. If you type "quit" at the console prompt, the console will quit, but your virtual machine and tasks will continue to run. At any command prompt on any host in the virtual machine, you can type

 % pvm

and you will get the message "pvm already running" and the console prompt. When you are finished with the virtual machine you should type

 pvm> halt

This command kills any PVM tasks, shuts down the virtual machine, and exits the console. This is the recommended method to stop PVM because it makes sure that the virtual machine shuts down cleanly.

You should practice starting and stopping and adding hosts to PVM until you are comfortable with the PVM console. A full description of the PVM console and its many command options is given in the documentation that comes with the PVM software.

If you don't wish to type in a bunch of hostnames each time, there is a hostfile option. You can list the hostnames in a file one per line and then type

 % pvm hostfile

PVM will then add all the listed hosts simultaneously before the console prompt appears. Several options can be specified on a per host basis in the hostfile, if you wish to customize your virtual machine for a particular application or environment.

PVM may also be started in other ways. The functions of the console and a performance monitor have been combined in a graphical user interface called XPVM, which is available from the PVM Web site. If XPVM has been installed at your site, then it can be used to start PVM. To start PVM with this interface, type

 % xpvm

The menu button labeled "hosts" will pull down a list of hosts you can add. If you click on a hostname, it is added, and an icon of the machine appears in an animation of the virtual machine. A host is deleted if you click on a hostname that is already in the virtual machine. On startup XPVM reads the file '$HOME/. xpvm_hosts', which is a list of hosts to display in this menu. Hosts without leading "&" are added all at once at startup.

The quit and halt buttons work just like the PVM console. If you quit XPVM and then restart it, XPVM will automatically display what the running virtual machine looks like. Practice starting and stopping and adding hosts with XPVM. If any errors occur, they should appear in the window where you started XPVM.

10.3.3 Running PVM Programs

This section describes how to compile and run the example programs supplied with the PVM software. These example programs make useful templates on which to base your own PVM programs.

The first step is to copy the example programs into your own area:

 % cp -r $PVM_ROOT/examples $HOME/pvm3/examples
 % cd $HOME/pvm3/examples

The examples directory contains a 'Makefile.aimk' and 'Readme' file that describe how to build the examples. PVM supplies an architecture-independent make, aimk, that automatically determines PVM_ARCH and links any operating system-specific libraries to your application. when you placed the 'cshrc.stub' in your '.cshrc' file, aimk was automatically added to your $PATH. Using aimk allows you to leave the source code and makefile unchanged as you compile across different architectures.

The master/worker programming model is the most popular model used in cluster computing. To compile the master/slave C example, type

 % aimk master slave

If you prefer to work with Fortran, compile the Fortran version with

 % aimk fmaster fslave

Depending on the location of PVM_ROOT, the INCLUDE statement at the top of the Fortran examples may need to be changed. If PVM_ROOT is not 'HOME/pvm3', then change the include to point to '$PVM_ROOT/include/f pvm3.h'. Note that PVM_ROOT is not expanded inside the Fortran, so you must insert the actual path.

The makefile moves the executables to '$HOME/pvm3/bin/PVM_ARCH', which is the default location where PVM will look for them on all hosts. If your file system is not common across all your cluster nodes, then you will have to copy these executables on all your nodes.

From one window start up PVM and configure some hosts. These examples are designed to run on any number of hosts, including one. In another window, cd to the location of the PVM executables and type

 % master

The program will ask about the number of tasks. This number does not have to match the number of hosts in these examples. Try several combinations.

The first example illustrates the ability to run a PVM program from a prompt on any host in the virtual machine. This is how you would run a serial a.out program on a front console of a cluster. The next example, which is also a master/slave model called codehitc, shows how to spawn PVM jobs from the PVM console and also from XPVM.

The model hitc illustrates dynamic load balancing using the pool of tasks paradigm. In this paradigm, the master program manages a large queue of tasks, always sending idle slave programs more work to do until the queue is empty. This paradigm is effective in situations where the hosts have very different computational powers because the least-loaded or more powerful hosts do more of the work and all the hosts stay busy until the end of the problem. To compile hitc, type

 % aimk hitc hitc_slave

Since hitc does not require any user input, it can be spawned directly from the PVM console. Start the PVM console, and add some cluster nodes. At the PVM console prompt, type

 pvm> spawn -> hitc

The "->" spawn option causes all the print statements in hitc and in the slaves to appear in the console window. This can be a useful feature when debugging your first few PVM programs. You may wish to experiment with this option by placing print statements in 'hitc.f' and 'hitc_slave.f' and recompiling.

10.3.4 PVM Console Details

The PVM console, called pvm, is a standalone PVM task that allows you to interactively start, query, and modify the virtual machine. The console may be started and stopped multiple times on any of the hosts in the virtual machine without affecting PVM or any applications that may be running.

When the console is started, pvm determines whether PVM is already running and, if not, automatically executes pvmd on this host, passing pvmd the command-line options and hostfile. Thus, PVM need not be running to start the console.

         pvm [-n<hostname>] [hostfile]

The -n option is useful for specifying another name for the master pvmd (in case hostname doesn't match the IP address you want). This feature becomes very useful with Beowulf clusters because the nodes of the cluster sometime are on their own network. In this case the front-end node will have two hostnames: one for the cluster and one for the external network. The -n option lets you specify the cluster name directly during PVM startup.

Once started, the console prints the prompt

 pvm>

and accepts commands from standard input. The available commands are as follows:

  • add followed by one or more hostnames (cluster nodes), adds these hosts to the virtual machine.

  • alias defines or lists command aliases.

  • conf lists the configuration of the virtual machine including hostname, pvmd task ID, architecture type, and a relative speed rating.

  • delete followed by one or more hostnames, deletes these hosts from the virtual machine. PVM processes still running on these hosts are lost .

  • echo echoes arguments.

  • halt kills all PVM processes including console and then shuts down PVM. All daemons exit.

  • help can be used to get information about any of the interactive commands. The help command may be followed by a command name that will list options and flags available for this command.

  • id prints console task id.

  • jobs lists running jobs.

  • kill can be used to terminate any PVM process.

  • mstat shows status of specified hosts.

  • ps -a lists all processes currently on the virtual machine, their locations, their task IDs, and their parents' task IDs.

  • pstat shows status of a single PVM process.

  • quit exits the console, leaving daemons and PVM jobs running.

  • reset kills all PVM processes except consoles, and resets all the internal PVM tables and message queues. The daemons are left in an idle state.

  • setenv displays or sets environment variables.

  • sig followed by a signal number and tid, sends the signal to the task.

  • spawn starts a PVM application. Options include the following:

    • -count shows the number of tasks; default is 1

    • -(host) spawn on host; default is any

    • -(PVM_ARCH) spawn of hosts of type PVM_ARCH

    • -? enable debugging

    • -> redirect task output to console

    • ->file redirect task output to file

    • ->>file redirect task output append to file

    • -@ trace job; display output on console

    • -@file trace job; output to file

  • unalias undefines command alias.

  • version prints version of PVM being used.

PVM supports the use of multiple consoles. It is possible to run a console on any host in an existing virtual machine and even multiple consoles on the same machine. It is possible to start up a console in the middle of a PVM application and check on its progress.

References

[1] Paul Albitz and Cricket Liu. DNS and BIND. O'Reilly & Associates, Inc., Sebastopol, CA 95472, 4th edition, 2001.

[2] Stephen F. Altschul,Thomas L. Madden,Alejandro A. Schaffer,Jinghui Shang,Zheng Zhang,Webb Miller, and David J. Lipman. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res., 25:3389–3402, 1997.

[3] Sridhar Anandakrishnan. Penguins everywhere: GNU/Linux in Antarctica. IEEE Software, 16(6):90–96, Nov/Dec 1999.

[4] E. Anderson,Z. Bai,C. Bischof,J. Demmel,J. Dongarra,J. Du Croz,A. Greenbaum,S. Hammarling,A. McKenney,S. Ostrouchov, and D. Sorensen. LAPACK Users' Guide. SIAM, Philadelphia, 1992.

[5] Thomas E. Anderson,Michael D. Dahlin,Jeanna M. Neefe,David A. Patterson,Drew S. Roselli, and Randolph Y. Wang. Serverless network file systems. ACM Transactions on Computer Systems, 14(1):41–79, February 1996.

[6] Aztec home page. http://www.cs.sandia.gov/CRF/aztec1.html.

[7] Zhaojun Bai,James Demmel,Jack Dongarra,Axel Ruhe, and Henk van der Vorst. Templates for the Solution of Algebraic Eigenvalue Problems, A Practical Guide. SIAM, 2000.

[8] Satish Balay,Kris Buschelman,William D. Gropp,Dinesh Kaushik,Matt Knepley,Lois Curfman McInnes,Barry F. Smith, and Hong Zhang. PETSc web page. http://www.mcs.anl.gov/petsc, 2001.

[9] Satish Balay,Kris Buschelman,William D. Gropp,Dinesh Kaushik,Matt Knepley,Lois Curfman McInnes,Barry F. Smith, and Hong Zhang. PETSc users manual. Technical Report ANL-95/11 - Revision 2.1.5, Argonne National Laboratory, 2002.

[10] Satish Balay,William D. Gropp,Lois Curfman McInnes, and Barry F. Smith. Efficient management of parallelism in object oriented numerical software libraries. In E. Arge, A. M. Bruaset, and H. P. Langtangen, editors, Modern Software Tools in Scientific Computing, pages 163-202. Birkhauser Press, 1997.

[11] Daniel J. Barrett and Richard Silverman. SSH, The Secure Shell: The Definitive Guide. O'Reilly & Associates, Inc., Sebastopol, CA 95472, 1st edition, 2001.

[12] Richard Barrett,Michael Berry,Tony F. Chan,James Demmel,June Donato,Jack Dongarra,Victor Eijkhout,Roldan Pozo,Charles Romine, and Henk van der Vorst. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. SIAM, Philadelphia PA, 1994. http://www.netlib.org/templates/.

[13] Luiz Andr?Barroso,Jeffrey Dean, and Urs H?zle. Web search for a planet: The Google cluster architecture. IEEE Micro, 2003.

[14] David M. Beazley. Python Essential Reference. New Riders Publishing, second edition, 2001.

[15] L.S. Blackford,J. Choi,A. Cleary,E. D'Azevedo,J. Demmel,I. Dhillon,J. Dongarra,S. Hammerling,G. Henry,A. Petitet,K. Stanley,D. Walker, and R.C. Whaley. ScaLAPACK Users' Guide. SIAM, 1997.

[16] BLAS web page. http://www.netlib.org/blas.

[17] Peter J. Braam. The Lustre storage architecture. Technical report, Cluster File Systems, Inc., 2003.

[18] Tim Bray. Bonnie file system benchmark. http://www.textuality.com/bonnie/.

[19] Ron Brightwell,Tramm Hudson,Arthur B. Maccabe, and Rolf Riesen. The Portals 3.0 message passing interface. Technical Report SAND99-2959, Sandia Technical Report, November 1999.

[20] Surendra Byna,William Gropp,Xian-He Sun, and Rajeev Thakur. Improving the performance of MPI derived datatypes by optimizing memory-access cost. Technical Report ANL/MCS-P1045-0403, Mathematics and Computer Science Division, Argonne National Laboratory, 2003.

[21] B. Callaghan,B. Pawlowski, and P. Staubach. NFS version 3 protocol specification. Technical Report RFC 1813, Sun Microsystems, Inc., June 1995.

[22] Philip H. Carns,Walter B. Ligon III,Robert B. Ross, and Rajeev Thakur. PVFS: A parallel file system for Linux clusters. In Proceedings of the 4th Annual Linux Showcase and Conference, pages 317–327, Atlanta, GA, October 2000. USENIX Association.

[23] CERT web site. http://www.cert.org.

[24] Chaco web page. http://www.cs.sandia.gov/~bahendr/chaco.html.

[25] Albert Cheng and Michael Folk. HDF5: High performance science data solution for the new millennium. In ACM, editor, SC2000: High Performance Networking and Computing. Dallas Convention Center, Dallas, TX, USA, November 4–10, 2000, pages 149–149, New York, NY 10036, USA and 1109 Spring Street, Suite 300, Silver Spring, MD 20910, USA, 2000. ACM Press and IEEE Computer Society Press.

[26] Averg Ching,Alok Choudhary,Kenin Coloma,Wei keng Liao,Robert Ross, and William Gropp. Noncontiguous I/O accesses through MPI-IO. In Proceedings of the Third IEEE/ACM International Symposium on Cluster Computing and the Grid (CCGrid2003), May 2003.

[27] Avery Ching,Alok Choudhary,Wei keng Liao,Robert Ross, and William Gropp. Noncontiguous I/O through PVFS. In Proceedings of the 2002 IEEE International Conference on Cluster Computing, September 2002.

[28] Douglas Comer. Internetworking with TCP/IP, Volume 1: Principles, Protocols, and Architecture. Prentice Hall, Inc., Englewood Cliffs, NJ 07632, 4th edition, 2000.

[29] Peter F. Corbett and Dror G. Feitelson. The Vesta parallel file system. In Hai Jin, Toni Cortes, and Rajkumar Buyya, editors, High Performance Mass Storage and Parallel I/O: Technologies and Applications, chapter 20, pages 285–308. IEEE Computer Society Press and Wiley, New York, NY, 2001.

[30] Cray Research. Application Programmer's Library Reference Manual, 2nd edition, November 1995. Publication SR-2165.

[31] David E. Culler,Richard M. Karp,David A. Patterson,Abhijit Sahay,Klaus E. Schauser,Eunice Santos,Ramesh Subramonian, and Thorsten von Eicken. LogP: towards a realistic model of parallel computation. ACM SIGPLAN Notices, 28(7):1–12, July 1993.

[32] I. S. Dhillon. A new O(n2) Algorithm for the Symmetric Tridiagonal Eigenvalue/Eigenvector Problem. PhD thesis, Computer Science Division, University of California, Berkeley, California, 1997.

[33] Chris DiBona,Sam Ockman, and Mark Stone. Open Sources: Voices from the Open Source Revolution. O'Reilly & Associates, Inc., 1999.

[34] Jack Dongarra. Performance of various computers using standard linear equations software. Technical Report Number CS-89-85, University of Tennessee, Knoxville TN, 37996, 2001. http://www.netlib.org/benchmark/performance.ps.

[35] Jack J. Dongarra,Iain S. Duff,Danny C. Sorensen, and Henk A. van der Vorst. Solving Linear Systems on Vector and Shared Memory Computers. SIAM, Philadelphia, 1991.

[36] R. Evard,N. Desai,J. Navarro, and D. Nurmi. Clusters as large-scale development facilities. In Proceedings of the 2002 IEEE International Conference on Cluster Computing, September 2002.

[37] FFTW web page. http://www.fftw.org.

[38] Fluent web page. http://www.fluent.com.

[39] G. C. Fox,S. W. Otto, and A. J. G. Hey. Matrix algorithms on a hypercube I: Matrix multiplication. Parallel Computing, 4:17–31, 1987.

[40] Matteo Frigo and Steven G. Johnson. FFTW: An adaptive software architecture for the FFT. In Proc. 1998 IEEE Intl. Conf. Acoustics Speech and Signal Processing, volume 3, pages 1381–1384. IEEE, 1998.

[41] The galley parallel file system. http://www.cs.dartmouth.edu/~dfk/nils//galley.html.

[42] Gaussian web page. http://www.gaussian.com.

[43] Al Geist,Adam Beguelin,Jack Dongarra,Weicheng Jiang,Bob Manchek, and Vaidy Sunderam. PVM: Parallel Virtual Machine—A User's Guide and Tutorial for Network Parallel Computing. MIT Press, Cambridge, Mass., 1994.

[44] W. Gropp and E. Lusk. Scalable Unix tools on parallel processors. In Proceedings of the Scalable High-Performance Computing Conference, May 23–25, 1994, Knoxville, Tennessee, pages 56–62, 1109 Spring Street, Suite 300, Silver Spring, MD 20910, USA, 1994. IEEE Computer Society Press.

[45] W. D. Gropp,D. K. Kaushik,D. E. Keyes, and B. F. Smith. Towards realistic performance bounds for implicit CFD codes. In Proceedings of Parallel CFD'99, pages 241–248, 1999.

[46] William Gropp,Steven Huss-Lederman,Andrew Lumsdaine,Ewing Lusk,Bill Nitzberg,William Saphir, and Marc Snir. MPI—The Complete Reference: Volume 2, The MPI-2 Extensions. MIT Press, Cambridge, MA, 1998.

[47] William Gropp,Ewing Lusk,Nathan Doss, and Anthony Skjellum. A high-performance, portable implementation of the MPI Message-Passing Interface standard. Parallel Computing, 22(6):789–828, 1996.

[48] William Gropp,Ewing Lusk, and Anthony Skjellum. Using MPI: Portable Parallel Programming with the Message Passing Interface, 2nd edition. MIT Press, Cambridge, MA, 1999.

[49] William Gropp,Ewing Lusk, and Debbie Swider. Improving the performance of MPI derived datatypes. In Anthony Skjellum, Purushotham V. Bangalore, and Yoginder S. Dandass, editors, Proceedings of the Third MPI Developer's and User's Conference, pages 25–30. MPI Software Technology Press, 1999.

[50] William Gropp,Ewing Lusk, and Rajeev Thakur. Using MPI-2: Advanced Features of the Message-Passing Interface. MIT Press, Cambridge, MA, 1999.

[51] William D. Gropp and Ewing Lusk. Reproducible measurements of MPI performance characteristics. In Jack Dongarra, Emilio Luque, and Tom? Margalef, editors, Recent Advances in Parallel Virtual Machine and Message Passing Interface, volume 1697 of Lecture Notes in Computer Science, pages 11–18. Springer Verlag, 1999. 6th European PVM/MPI Users' Group Meeting, Barcelona, Spain, September 1999.

[52] Michael Hasenstein. The logical volume manager (LVM). Technical Report Whitepaper, SuSE Inc., 2001.

[53] Don Heller. Rabbit: A performance counters library for Intel/AMD processors and Linux. www.scl.ameslab.gov/Projects/Rabbit/.

[54] J. M. D. Hill,B. McColl,D. C. Stefanescu,M. W. Goudreau,K. Lang,S. B. Rao,T. Suel,T. Tsantilas, and R. H. Bisseling. BSPlib: The BSP programming library. Parallel Computing, 24(14):1947–1980, December 1998.

[55] James V. Huber, Jr.,Christopher L. Elford,Daniel A. Reed,Andrew A. Chien, and David S. Blumenthal. PPFS: A high performance portable parallel file system. In Hai Jin, Toni Cortes, and Rajkumar Buyya, editors, High Performance Mass Storage and Parallel I/O: Technologies and Applications, chapter 22, pages 330–343. IEEE Computer Society Press and Wiley, New York, NY, 2001.

[56] Craig Hunt. TCP/IP Network Administration. O'Reilly & Associates, Inc., Sebastopol, CA 95472, 3rd edition, 2002.

[57] S. A. Hutchinson,J. N. Shadid, and R. S. Tuminaro. Aztec user's guide: Version 1.1. Technical Report SAND95-1559, Sandia National Laboratories, 1995.

[58] IEEE/ANSI Std. 1003.1. Portable operating system interface (POSIX)-part 1: System application program interface (API) [C language], 1996 edition.

[59] Iperf home page. http://dast.nlanr.net/projects/iperf.

[60] Alan H. Karp. Bit reversal on uniprocessors. SIAM Review, 38(1): 1–26, March 1996.

[61] Jeffrey Kephart and David Chess. The vision of autonomic computing. IEEE Computer, pages 41–50, January 2003.

[62] David Kotz. Disk-directed I/O for MIMD multiprocessors. In Hai Jin, Toni Cortes, and Rajkumar Buyya, editors, High Performance Mass Storage and Parallel I/O: Technologies and Applications, chapter 35, pages 513–535. IEEE Computer Society Press and John Wiley & Sons, 2001.

[63] LAPACK software. http://www.netlib.org/lapack.

[64] C. Lawson,R. Hanson,D. Kincaid, and F. Krogh. Basic linear algebra subprograms for FORTRAN usage. Transactions on Mathematical Software, 5:308–323, 1979.

[65] Edward K. Lee and Chandramohan A. Thekkath. Petal: Distributed virtual disks. In Proceedings of the Seventh International Conference on Architectural Support for Programming Languages and Operating Systems, pages 84–92, Cambridge, MA, October 1996.

[66] J. Li,W.-K. Liao,A. Choudhary,R. Ross,R. Thakur,W. Gropp, and R. Latham. Parallel netCDF: A scientific high-performance I/O interface. Technical Report ANL/MCS-P1048-0503, Mathematics and Computer Science Division, Argonne National Laboratory, May 2003.

[67] Xiaoye S. Li. Sparse Gaussian Eliminiation on High Performance Computers. PhD thesis, University of California at Berkeley, 1996.

[68] Josip Loncaric. Linux 2.2.12 TCP performance fix for short messages. www.icase.edu/coral/LinuxTCP2.html. This web site is no longer available.

[69] LS-Dyna web page. http://www.lstc.com.

[70] Alex Martelli and David Ascher, editors. Python Cookbook. O'Reilly and Associates, 2002.

[71] John D. McCalpin. STREAM: Sustainable memory bandwidth in high performance computers. http://www.cs.virginia.edu/stream/.

[72] Message Passing Interface Forum. MPI: A Message-Passing Interface standard. International Journal of Supercomputer Applications, 8(3/4):165–414, 1994.

[73] Message Passing Interface Forum. MPI2: A message passing interface standard. International Journal of High Performance Computing Applications, 12(1–2):1–299, 1998.

[74] Jeffrey Mogul and Steve Deering. Path MTU discovery. Technical Report IETF RFC 1191, Digital Equipment Corporation WRL and Stanford University, November 1990. http://www.ietf.org/rfc/rfc1191.txt.

[75] P. Mucci,S. Brown,C. Deane, and G. Ho. Papi: A portable interface to hardware performance counters. icl.cs.utk.edu/projects/papi/.

[76] NAMD web page. http://www.ks.uiuc.edu/Research/namd/.

[77] Nastran web page. http://www.mscsoftware.com/products/products_detail.cfm?S=74&PI=7&M=0.

[78] Nils Nieuwejaar and David Kotz. The Galley parallel file system. Parallel Computing, 23(4):447–476, June 1997.

[79] Nils Nieuwejaar,David Kotz,Apratim Purakayastha,Carla Schlatter Ellis, and Michael Best. File-access characteristics of parallel scientific workloads. IEEE Transactions on Parallel and Distributed Systems, 7(10):1075–1089, October 1996.

[80] Bill Nowicki. NFS: Network file system protocol specification. Technical Report RFC 1094, Sun Microsystems, Inc., March 1989.

[81] NWChem web page. http://www.emsl.pnl.gov:2080/docs/nwchem/nwchem.html.

[82] Emil Ong,Ewing Lusk, and William Gropp. Scalable Unix commands for parallel processors: A high-performance implementation. In Jack Dongarra and Yiannis Cotronis, editors, Proceedings of Euro PVM/MPI. Springer Verlag, 2001.

[83] OpenMP Web page. www.openmp.org.

[84] ParMetis web page. http://www-users.cs.umn.edu/~karypis/metis/parmetis/index.html.

[85] Chrisila Pettey,Ralph Butler,Brad Rudnik, and Thomas Naughton. A rapid recovery Beowulf platform. In Henry Selvaraj and Venkatesan Muthukumar, editors, Proceedings of Fifteenth International Conference on Systems Engineering, pages 278–283, 2002.

[86] PLAPACK web page. http://www.cs.utexas.edu/users/plapack/.

[87] Jon Postel, editor. Transmission control protocol. Technical Report IETF RFC 793, Information Sciences Institute, University of Southern California, September 1981. http://www.ietf.org/rfc/rfc0793.txt.

[88] Kenneth W. Preslan,Andrew Barry,Jonathan E. Brassow,Russell Cattlelan,Adam Manthei,Erling Nygaard,Seth Van Oort,David C. Teigland,Mike Tilstra, Matthew O'Keefe,Grant Erickson, and Manish Agarwal. A 64-bit, shared disk file system for Linux. In Proceedings of the Eighth NASA Goddard Conference on Mass Storage Systems and Technologies, March 2000.

[89] Kenneth W. Preslan,Andrew P. Barry,Jonathan E. Brassow,Grant M. Erickson,Erling Nygaard,Christopher J. Sabol,Steven R. Soltis,David C. Teigland, and Matthew T. O'Keefe. A 64-bit, shared disk file system for Linux. In Proceedings of the Seventh NASA Goddard Conference on Mass Storage Systems, pages 22–41, San Diego, CA, March 1999. IEEE Computer Society Press.

[90] The parallel virtual file system. http://www.pvfs.org.

[91] Using the parallel virtual file system. http://www.parl.clemson.edu/pvfs/user-guide.html.

[92] QBank: A CPU allocations bank. http://www.emsl.pnl.gov:2080/docs/mscf/qbank-2.10/.

[93] Red Hat Linux 9: Red Hat Linux Customization Guide. Red Hat web site. http://www.redhat.com/docs/manuals/linux/RHL-9-Manual/pdf/rhl-cg-en-9.p%df.

[94] R. Reussner,P. Sanders,L. Prechelt, and M Mller. SKaMPI: A detailed, accurate MPI benchmark. In Vassuk Alexandrov and Jack Dongarra, editors, Recent advances in Parallel Virtual Machine and Message Passing Interface, volume 1497 of Lecture Notes in Computer Science, pages 52–59. Springer Verlag, 1998. 5th European PVM/MPI Users' Group Meeting.

[95] R. K. Rew and G. P. Davis. The unidata netCDF: Software for scientific data access. Sixth Int'l. Conf. on Interactive Inf. and Processing Sys. for Meteorology, Oceanography, and Hydrology, February 1990.

[96] R. Ross,D. Nurmi,A. Cheng, and M. Zingale. A case study in application I/O on linux clusters. In Proceedings of SC2001, November 2001.

[97] Robert B. Ross. Reactive Scheduling for Parallel I/O Systems. PhD thesis, Dept. of Electrical and Computer Engineering, Clemson University, Clemson, SC, December 2000.

[98] Youcef Saad. Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia, PA, 2003. Originally published by PWS Publishing Company, Boston, 1996; this edition is available for download from http://www.cs.umn.edu/~saad.

[99] K. Schloegel,G. Karypis, and V. Kumar. Parallel multilevel algorithms for multi-constraint graph partitioning. In Proceedings of EuroPar-2000, 2000.

[100] Frank Schmuck and Roger Haskin. GPFS: A shared-disk file system for large computing clusters. In First USENIX Conference on File and Storage Technologies (FAST'02), Monterey, CA, January 28–30 2002.

[101] SecurityFocus web site. http://www.securityfocus.org.

[102] S. Shepler,B. Callaghan,D. Robinson,R. Thurlow,C. Beame,M. Eisler, and D. Noveck. NFS version 4 protocol. Technical Report RFC 3010, Sun Microsystems, Inc., Hummingbird Ltd., Zambeel, Inc., and Network Appliance, Inc., December 2000.

[103] Joseph D. Sloan. Network Troubleshooting Tools. O'Reilly & Associates, 2001.

[104] Quinn O. Snell,Armin R. Mikler, and John L. Gustafson. NetPIPE: A network protocol independent performace evaluator. In IASTED International Conference on Intelligent Information Management and Systems, June 1996. http://www.scl.ameslab.gov/netpipe/paper/netpipe.ps.

[105] Marc Snir,Steve W. Otto,Steven Huss-Lederman,David W. Walker, and Jack Dongarra. MPI—The Complete Reference: Volume 1, The MPI Core, 2nd edition. MIT Press, Cambridge, MA, 1998.

[106] D. C. Sorensen. Implicit application of polynomial filters in a k-step Arnoldi method. SIAM J. Matrix Anal., 13:357–385, 1992.

[107] T. Sterling,D. Savarese,D. J. Becker,J. E. Dorband,U. A. Ranawake, and C. V. Packer. BEOWULF : A parallel workstation for scientific computation. In International Conference on Parallel Processing, Vol.1: Architecture, pages 11–14, Boca Raton, USA, August 1995. CRC Press.

[108] Thomas L. Sterling,John Salmon,Donald J. Becker, and Daniel F. Savarese. How to Build a Beowulf. MIT Press, 1999.

[109] Hal Stern,Mike Eisler, and Ricardo Labiaga. Managing NFS and NIS. O'Reilly & Associates, Inc., Sebastopol, CA 95472, 2nd edition, 2001.

[110] W. Richard Stevens. TCP/IP Illustrated, Volume 1: The Protocols. Addison-Wesley Publishing Company, Reading, MA 01867, 1994.

[111] W. Richard Stevens. UNIX network programming: Networking APIs: Sockets and XTI, volume 1. Prentice-Hall PTR, Upper Saddle River, NJ 07458, USA, second edition, 1998.

[112] SuperLU web page. http://www.nersc.gov/~xiaoye/SuperLU/.

[113] Rajeev Thakur and Alok Choudhary. An Extended Two-Phase Method for Accessing Sections of Out-of-Core Arrays. Scientific Programming, 5(4):301–317, Winter 1996.

[114] Rajeev Thakur,Alok Choudhary,Rajesh Bordawekar,Sachin More, and Sivaramakrishna Kuditipudi. Passion: Optimized I/O for parallel applications. IEEE Computer, 29(6):70–78, June 1996.

[115] Rajeev Thakur,William Gropp, and Ewing Lusk. On implementing MPI-IO portably and with high performance. In Proceedings of the 6th Workshop on I/O in Parallel and Distributed Systems, pages 23–32. ACM Press, May 1999.

[116] Rajeev Thakur,Ewing Lusk, and William Gropp. A case for using MPI's derived datatypes to improve I/O performance. In Proceedings of SC98: High Performance Networking and Computing, November 1998.

[117] Rajeev Thakur,Robert Ross,Ewing Lusk, and William Gropp. Users guide for ROMIO: A high-performance, portable MPI-IO implementation. Technical Report ANL/MCS Technical Memorandum No. 234, Mathematics and Computer Science Division, Argonne National Laboratory, May 2002.

[118] C. Thekkath,T. Mann, and E. Lee. Frangipani: A scalable distributed file system. In Proceedings of the Sixteenth ACM Symposium on Operating System Principles (SOSP), October 1997.

[119] TotalView Multiprocess Debugger/Analyzer, 2000. www.etnus.com/Products/TotalView.

[120] J. L. Traeff,R. Hempel,H. Ritzdoff, and F. Zimmermann. Flattening on the fly: Efficient handling of MPI derived datatypes. In J. J. Dongarra, E. Luque, and Tomas Margalef, editors, Recent Advances in Parallel Virtual Machine and Message Passing Interface: 6th European PVM/MPI Users' Group Meeting, volume 1697 of Lecture Notes in Computer Science, pages 109–116. Springer Verlag, 1999.

[121] The treadmarks distributed shared memory (DSM) system. www.cs.rice.edu/~willy/TreadMarks/overview.html.

[122] Trilinos web page. http://software.sandia.gov/trilinos/index.html.

[123] M. Vilayannur,A. Sivasubramaniam,M. Kandemir,R. Thakur, and R. Ross. Discretionary caching for I/O on clusters. In Proceedings of the Third IEEE/ACM International Symposium on Cluster Computing and the Grid (CCGrid2003), May 2003.

[124] Larry Wall,Tom Christiansen, and Jon Orwant. Programming Perl. O'Reilly and Associates, third edition, 2000.

[125] R. Clint Whaley,Antoine Petitet, and Jack J. Dongarra. Automated empirical optimizations of software and the ATLAS project. Parallel Computing, 27(1–2):3–35, January 2001.

[126] Omer Zaki,Ewing Lusk,William Gropp, and Deborah Swider. Toward scalable performance visualization with Jumpshot. High Performance Computing Applications, 13(2):277–288, Fall 1999.

[127] Robert L. Ziegler. Linux Firewalls. New Riders Publishing, 2nd edition, 2001.

[128] Zoltan web page. http://www.cs.sandia.gov/Zoltan/.

Оставьте свой комментарий !

Ваше имя:
Комментарий:
Оба поля являются обязательными

 Автор  Комментарий к данной статье