Шаблоны и наследование
Именованные шаблонные аргументы
Параметр шаблона может иметь значение по умолчанию - пример :
template<typename Policy1 = DefaultPolicy1,
typename Policy2 = DefaultPolicy2,
typename Policy3 = DefaultPolicy3,
typename Policy4 = DefaultPolicy4>
class BreadSlicer {
…
};
Предпочтительнее использовать конструкцию BreadSlicer<Policy3 = Custom> чем
BreadSlicer<DefaultPolicy1, DefaultPolicy2, Custom>.
Такая техника более понятна.
Техника заключается в размешении значений по умолчанию в базовых классах и перегрузки их через наследование.
Вместо прямого определения , мы делаем это через helper-классы.
Например можно написать BreadSlicer<Policy3_is<Custom> >.
Любой шаблонный аргумент может быть описан в любом из policies:
template <typename PolicySetter1 = DefaultPolicyArgs,
typename PolicySetter2 = DefaultPolicyArgs,
typename PolicySetter3 = DefaultPolicyArgs,
typename PolicySetter4 = DefaultPolicyArgs>
class BreadSlicer {
typedef PolicySelector<PolicySetter1, PolicySetter2,
PolicySetter3, PolicySetter4>
Policies;
// use Policies::P1, Policies::P2, … to refer to the various policies
…
};
Шаблон PolicySelector обьединяет различные аргументы в один тип ,
который перегружает тип по умолчанию - это делается с помощью наследования :
// PolicySelector<A,B,C,D> creates A,B,C,D as base classes
// Discriminator<> allows having even the same base class more than once
template<typename Base, int D>
class Discriminator : public Base {
};
template <typename Setter1, typename Setter2,
typename Setter3, typename Setter4>
class PolicySelector : public Discriminator<Setter1,1>,
public Discriminator<Setter2,2>,
public Discriminator<Setter3,3>,
public Discriminator<Setter4,4> {
};
Дефолтовые значения мы собираем в базовом классе :
// name default policies as P1, P2, P3, P4
class DefaultPolicies {
public:
typedef DefaultPolicy1 P1;
typedef DefaultPolicy2 P2;
typedef DefaultPolicy3 P3;
typedef DefaultPolicy4 P4;
};
Базовый класс должен быть унаследован виртуально:
// class to define a use of the default policy values
// avoids ambiguities if we derive from DefaultPolicies more than once
class DefaultPolicyArgs : virtual public DefaultPolicies {
};
Еще несколько шаблонов для перегрузки :
template <typename Policy>
class Policy1_is : virtual public DefaultPolicies {
public:
typedef Policy P1; // overriding typedef
};
template <typename Policy>
class Policy2_is : virtual public DefaultPolicies {
public:
typedef Policy P2; // overriding typedef
};
template <typename Policy>
class Policy3_is : virtual public DefaultPolicies {
public:
typedef Policy P3; // overriding typedef
};
template <typename Policy>
class Policy4_is : virtual public DefaultPolicies {
public:
typedef Policy P4; // overriding typedef
};
Теперь создаем экземпляр BreadSlicer<> :
BreadSlicer<Policy3_is<CustomPolicy> > bc;
Для этого BreadSlicer<> тип Policies определим как
PolicySelector<Policy3_is<CustomPolicy>,
DefaultPolicyArgs,
DefaultPolicyArgs,
DefaultPolicyArgs>
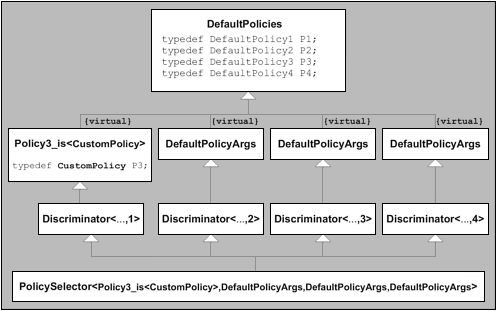
С помощью класса шаблона Discriminator<> получена иерархия,
в которой все шаблонные аргументы находятся в базовом классе
(Figure 16.1).
Эти базовые классы происходят от DefaultPolicies,
который определяет типы по умолчанию для P1, P2, P3, и P4.
Внутри шаблона BreadSlicer
вы можете ссылаться на 4 policies типа : Policies::P3. Например:
template <... >
class BreadSlicer {
…
public:
void print () {
Policies::P3::doPrint();
}
…
};
В исходнике inherit/namedtmpl.cpp вы можете найти полный пример.
|
Оптимизация пустых базовых классов - Empty Base Class Optimization (EBCO)
C++ classes are often "empty," which means that their internal representation does not require any bits of memory at run time. This is the case typically for classes that contain only type members, nonvirtual function members, and static data members. Nonstatic data members, virtual functions, and virtual base classes, on the other hand, do require some memory at run time.
Even empty classes, however, have nonzero size. Try the following program if you'd like to verify this:
// inherit/empty.cpp
#include <iostream>
class EmptyClass {
};
int main()
{
std::cout << "sizeof(EmptyClass): " << sizeof(EmptyClass)
<< '\n';
}
For many platforms, this program will print 1 as size of EmptyClass. A few systems impose more strict alignment requirements on class types and may print another small integer (typically, 4).
16.2.1 Layout Principles
The designers of C++ had various reasons to avoid zero-size classes. For example, an array of zero-size classes would presumably have size zero too, but then the usual properties of pointer arithmetic would not apply anymore. For example, let's assume ZeroSizedT is a zero-size type:
ZeroSizedT z[10];
…
&z[i] - &z[j] // compute distance between pointers/addresses
Normally, the difference in the previous example is obtained by dividing the number of bytes between the two addresses by the size of the type to which it is pointing, but when that size is zero this is clearly not satisfactory.
However, even though there are no zero-size types in C++, the C++ standard does specify that when an empty class is used as a base class, no space needs to be allocated for it provided that it does not cause it to be allocated to the same address as another object or subobject of the same type. Let's look at some examples to clarify what this so-called empty base class optimization (or EBCO) means in practice. Consider the following program:
// inherit/ebco1.cpp
#include <iostream>
class Empty {
typedef int Int; // typedef members don't make a class nonempty
};
class EmptyToo : public Empty {
};
class EmptyThree : public EmptyToo {
};
int main()
{
std::cout << "sizeof(Empty): " << sizeof(Empty)
<< '\n';
std::cout << "sizeof(EmptyToo): " << sizeof(EmptyToo)
<< '\n';
std::cout << "sizeof(EmptyThree): " << sizeof(EmptyThree)
<< '\n';
}
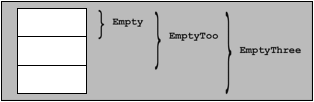
If your compiler implements the empty base optimization, it will print the same size for every class, but none of these classes has size zero (see Figure 16.2). This means that within class EmptyToo, the class Empty is not given any space. Note also that an empty class with optimized empty bases (and no other bases) is also empty. This explains why class EmptyThree can also have the same size as class Empty. If your compiler does not implement the empty base optimization, it will print different sizes (see Figure 16.3).

// inherit/ebco2.cpp
#include <iostream>
class Empty {
typedef int Int; // typedef members don't make a class nonempty
};
class EmptyToo : public Empty {
};
class NonEmpty : public Empty, public EmptyToo {
};
int main()
{
std::cout << "sizeof(Empty): " << sizeof(Empty) << '\n';
std::cout << "sizeof(EmptyToo): " << sizeof(EmptyToo) << '\n';
std::cout << "sizeof(NonEmpty): " << sizeof(NonEmpty) << '\n';
}
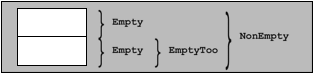
It may come as a surprise that class NonEmpty is not an empty class After all, it does not have any members and neither do its base classes. However, the base classes Empty and EmptyToo of NonEmpty cannot be allocated to the same address because this would cause the base class Empty of EmptyToo to end up at the same address as the base class Empty of class NonEmpty. In other words, two subobjects of the same type would end up at the same offset, and this is not permitted by the object layout rules of C++. It may be conceivable to decide that one of the Empty base subobjects is placed at offset "0 bytes" and the other at offset "1 byte," but the complete NonEmpty object still cannot have a size of one byte because in an array of two NonEmpty objects, an Empty subobject of the first element cannot end up at the same address as an Empty subobject of the second element (see Figure 16.4).
The rationale for the constraint on empty base optimization stems from the fact that it is desirable to be able to compare whether two pointers point to the same object. Because pointers are nearly always internally represented as just addresses, we must ensure that two different addresses (that is, pointer values) correspond to two different objects.
The constraint may not seem very significant. However, in practice, it is often encountered because many classes tend to inherit from a small set of empty classes that define some common typedefs. When two subobjects of such classes are used in the same complete object, the optimization is inhibited.
16.2.2 Members as Base Classes
The empty base class optimization has no equivalent for data members because (among other things) it would create some problems with the representation of pointers to members. As a result, it is sometimes desirable to implement as a (private) base class what would at first sight be thought of as a member variable. However, this is not without its challenges.
The problem is most interesting in the context of templates because template parameters are often substituted with empty class types, but in general one cannot rely on this rule. If nothing is known about a template type parameter, empty base optimization cannot easily be exploited. Indeed, consider the following trivial example:
template <typename T1, typename T2>
class MyClass {
private:
T1 a;
T2 b;
…
};
It is entirely possible that one or both template parameters are substituted by an empty class type. If this is the case, then the representation of MyClass<T1,T2> may be suboptimal and may waste a word of memory for every instance of a MyClass<T1,T2>.
This can be avoided by making the template arguments base classes instead:
template <typename T1, typename T2>
class MyClass : private T1, private T2 {
};
However, this straightforward alternative has its own set of problems. It doesn't work when T1 or T2 is substituted with a nonclass type or with a union type. It also doesn't work when the two parameters are substituted with the same type (although this can be addressed fairly easily by adding another layer of inheritance; see page 287 or page 449). However, even if we satisfactorily addressed these problems, a very serious problem persists: Adding a base class can fundamentally modify the interface of the given class. For our MyClass class, this may not seem very significant because there are very few interface elements to affect, but as we see later in this chapter, inheriting from a template parameter can affect whether a member function is virtual. Clearly, this approach to exploiting EBCO is fraught with all kinds of trouble.
A more practical tool can be devised for the common case when a template parameter is known to be substituted by class types only and when another member of the class template is available. The main idea is to "merge" the potentially empty type parameter with the other member using EBCO. For example, instead of writing
template <typename CustomClass>
class Optimizable {
private:
CustomClass info; // might be empty
void* storage;
…
};
a template implementer would use the following:
template <typename CustomClass>
class Optimizable {
private:
BaseMemberPair<CustomClass, void*> info_and_storage;
…
};
Even without seeing the implementation of the template BaseMemberPair, it is clear that its use makes the implementation of Optimizable more verbose. However, various template library implementers have reported that the performance gains (for the clients of their libraries) do justify the added complexity.
The implementation of BaseMemberPair can be fairly compact:
// inherit/basememberpair.hpp
#ifndef BASE_MEMBER_PAIR_HPP
#define BASE_MEMBER_PAIR_HPP
template <typename Base, typename Member>
class BaseMemberPair : private Base {
private:
Member member;
public:
// constructor
BaseMemberPair (Base const & b, Member const & m)
: Base(b), member(m) {
}
// access base class data via first()
Base const& first() const {
return (Base const&)*this;
}
Base& first() {
return (Base&)*this;
}
// access member data via second()
Member const& second() const {
return this->member;
}
Member& second() {
return this->member;
}
};
#endif // BASE_MEMBER_PAIR_HPP
An implementation needs to use the member functions first() and second() to access the encapsulated (and possibly storage-optimized) data members.
|
16.3 The Curiously Recurring Template Pattern (CRTP)
This oddly named pattern refers to a general class of techniques that consists of passing a derived class as a template argument to one of its own base classes. In its simplest form, C++ code for such a pattern looks as follows:
template <typename Derived>
class CuriousBase {
…
};
class Curious : public CuriousBase<Curious> {
…
};
Our first outline of CRTP shows a nondependent base class: The class Curious is not a template and is therefore immune to some of the name visibility issues of dependent base classes. However, this is not an intrinsic characteristic of CRTP. Indeed, we could just as well have used the following alternative outline:
template <typename Derived>
class CuriousBase {
…
};
template <typename T>
class CuriousTemplate : public CuriousBase<CuriousTemplate<T> > {
…
};
From this outline, however, it is not a far stretch to propose yet another alternative formulation, this time involving a template template parameter:
template <template<typename> class Derived>
class MoreCuriousBase {
…
};
template <typename T>
class MoreCurious : public MoreCuriousBase<MoreCurious> {
…
};
A simple application of CRTP consists of keeping track of how many objects of a certain class type were created. This is easily achieved by incrementing an integral static data member in every constructor and decrementing it in the destructor. However, having to provide such code in every class is tedious. Instead, we can write the following template:
// inherit/objectcounter.hpp
#include <stddef.h>
template <typename CountedType>
class ObjectCounter {
private:
static size_t count; // number of existing objects
protected:
// default constructor
ObjectCounter() {
++ObjectCounter<CountedType>::count;
}
// copy constructor
ObjectCounter (ObjectCounter<CountedType> const&) {
++ObjectCounter<CountedType>::count;
}
// destructor
~ObjectCounter() {
--ObjectCounter<CountedType>::count;
}
public:
// return number of existing objects:
static size_t live() {
return ObjectCounter<CountedType>::count;
}
};
// initialize counter with zero
template <typename CountedType>
size_t ObjectCounter<CountedType>::count = 0;
If we want to count the number of live (that is, not yet destroyed) objects for a certain class type, it suffices to derive the class from the ObjectCounter template. For example, we can define and use a counted string class along the following lines:
// inherit/testcounter.cpp
#include "objectcounter.hpp"
#include <iostream>
template <typename CharT>
class MyString : public ObjectCounter<MyString<CharT> > {
…
};
int main()
{
MyString<char> s1, s2;
MyString<wchar_t> ws;
std::cout << "number of MyString<char>: "
<< MyString<char>::live() << std::endl;
std::cout << "number of MyString<wchar_t>: "
<< ws.live() << std::endl;
}
In general, CRTP is useful to factor out implementations of interfaces that can only be member functions (for example, constructor, destructors, and subscript operators).

|
16.4 Parameterized Virtuality
C++ allows us to parameterize directly three kinds of entities through templates: types, constants ("nontypes"), and templates. However, indirectly, it also allows us to parameterize other attributes such as the virtuality of a member function. A simple example shows this rather surprising technique:
// inherit/virtual.cpp
#include <iostream>
class NotVirtual {
};
class Virtual {
public:
virtual void foo() {
}
};
template <typename VBase>
class Base : private VBase {
public:
// the virtuality of foo() depends on its declaration
// (if any) in the base class VBase
void foo() {
std::cout << "Base::foo()" << '\n';
}
};
template <typename V>
class Derived : public Base<V> {
public:
void foo() {
std::cout << "Derived::foo()" << '\n';
}
};
int main()
{
Base<NotVirtual>* p1 = new Derived<NotVirtual>;
p1->foo(); // calls Base::foo()
Base<Virtual>* p2 = new Derived<Virtual>;
p2->foo(); // calls Derived::foo()
}
This technique can provide a tool to design a class template that is usable both to instantiate concrete classes and to extend using inheritance. However, it is rarely sufficient just to sprinkle virtuality on some member functions to obtain a class that makes a good base class for more specialized functionality. This sort of development method requires more fundamental design decisions. It is therefore usually more practical to design two different tools (class or class template hierarchies) rather than trying to integrate them all into one template hierarchy.

|
16.5 Afternotes
Named template arguments are used to simplify certain class templates in the Boost library. Boost uses metaprogramming to create a type with properties similar to our PolicySelector (but without using virtual inheritance). The simpler alternative presented here was developed by one of us (Vandevoorde).
CRTPs have been in use since at least 1991. However, James Coplien was first to describe them formally as a class of so-called patterns (see [CoplienCRTP]). Since then, many applications of CRTP have been published. The phrase parameterized inheritance is sometimes wrongly equated with CRTP. As we have shown, CRTP does not require the derivation to be parameterized at all, and many forms of parameterized inheritance do not conform to CRTP. CRTP is also sometimes confused with the Barton-Nackman trick (see Section 11.7 on page 174) because Barton and Nackman frequently used CRTP in combination with friend name injection (and the latter is an important component of the Barton-Nackman trick). Our ObjectCounter example is almost identical to a technique developed by Scott Meyers in [MeyersCounting].
Bill Gibbons was the main sponsor behind the introduction of EBCO into the C++ programming language. Nathan Myers made it popular and proposed a template similar to our BaseMemberPair to take better advantage of it. The Boost library contains a considerably more sophisticated template, called compressed_pair, that resolves some of the problems we reported for the MyClass template in this chapter. boost::compressed_pair can also be used instead of our BaseMemberPair.

|
Chapter 17. Metaprograms
Metaprogramming consists of "programming a program." In other words, we lay out code that the programming system executes to generate new code that implements the functionality we really want. Usually the term metaprogramming implies a reflexive attribute: The metaprogramming component is part of the program for which it generates a bit of code/program.
Why would metaprogramming be desirable? As with most other programming techniques, the goal is to achieve more functionality with less effort, where effort can be measured as code size, maintenance cost, and so forth. What characterizes metaprogramming is that some user-defined computation happens at translation time. The underlying motivation is often performance (things computed at translation time can frequently be optimized away) or interface simplicity (a metaprogram is generally shorter than what it expands to) or both.
Metaprogramming often relies on the concepts of traits and type functions as developed in Chapter 15. We therefore recommend getting familiar with that chapter prior to delving into this one.
|
17.1 A First Example of a Metaprogram
In 1994 during a meeting of the C++ standardization committee, Erwin Unruh discovered that templates can be used to compute something at compile time. He wrote a program that produced prime numbers. The intriguing part of this exercise, however, was that the production of the prime numbers was performed by the compiler during the compilation process and not at run time. Specifically, the compiler produced a sequence of error messages with all prime numbers from two up to a certain configurable value. Although this program wasn't strictly portable (error messages aren't standardized), the program did show that the template instantiation mechanism is a primitive recursive language that can perform nontrivial computations at compile time. This sort of compile-time computation that occurs through template instantiation is commonly called template metaprogramming.
As an introduction to the details of metaprogramming we start with a simple exercise (we will show Erwin's prime number program later on page 318). The following program shows how to compute at compile time the power of three for a given value:
// meta/pow3.hpp
#ifndef POW3_HPP
#define POW3_HPP
// primary template to compute 3 to the Nth
template<int N>
class Pow3 {
public:
enum { result=3*Pow3<N-1>::result };
};
// full specialization to end the recursion
template<>
class Pow3<0> {
public:
enum { result = 1 };
};
#endif // POW3_HPP
The driving force behind template metaprogramming is recursive template instantiation.
In our program to compute 3N
, recursive template instantiation is driven by the following two rules:
3N
= 3 * 3N
-1 30 = 1
The first template implements the general recursive rule:
template<int N>
class Pow3 {
public:
enum { result = 3 * Pow3<N-1>::result };
};
When instantiated over a positive integer N, the template Pow3<> needs to compute the value for its enumeration value result. This value is simply twice the corresponding value in the same template instantiated over N-1.
The second template is a specialization that ends the recursion. It establishes the result of Pow3<0>:
template<>
class Pow3<0> {
public:
enum { result = 1 };
};
Let's study the details of what happens when we use this template to compute 37 by instantiating Pow3<7>:
// meta/pow3.cpp
#include <iostream>
#include "pow3.hpp"
int main()
{
std::cout << "Pow3<7>::result = " << Pow3<7>::result
<< '\n';
}
First, the compiler instantiates Pow3<7>. Its result is
3 * Pow3<6>::result
Thus, this requires the instantiation of the same template for 6. Similarly, the result of Pow3<6> instantiates Pow3<5>, Pow3<4>, and so forth. The recursion stops when Pow3<> is instantiated over zero which yields one as its result.
The Pow3<> template (including its specialization) is called a template metaprogram. It describes a bit of computation that is evaluated at translation time as part of the template instantiation process. It is relatively simple and may not look very useful at first, but there are situations when such a tool comes in very handy.
|
17.2 Enumeration Values versus Static Constants
In old C++ compilers, enumeration values were the only available possibility to have "true constants" (so-called constant-expressions) inside class declarations. However, this has changed during the standardization of C++, which introduced the concept of in-class static constant initializers. A brief example illustrates the construct:
struct TrueConstants {
enum { Three = 3 };
static int const Four = 4;
};
In this example, Four is a "true constant"just as is Three.
With this, our Pow3 metaprogram may also look as follows:
// meta/pow3b.hpp
#ifndef POW3_HPP
#define POW3_HPP
// primary template to compute 3 to the Nth
template<int N>
class Pow3 {
public:
static int const result = 3 * Pow3<N-1>::result;
};
// full specialization to end the recursion
template<>
class Pow3<0> {
public:
static int const result = 1;
};
#endif // POW3_HPP
The only difference is the use of static constant members instead of enumeration values. However, there is a drawback with this version: Static constant members are lvalues. So, if you have a declaration such as
void foo(int const&);
and you pass it the result of a metaprogram
foo(Pow3<7>::result);
a compiler must pass the address of Pow3<7>::result, which forces the compiler to instantiate and allocate the definition for the static member. As a result, the computation is no longer limited to a pure "compile-time" effect.
Enumeration values aren't lvalues (that is, they don't have an address). So, when you pass them "by reference," no static memory is used. It's almost exactly as if you passed the computed value as a literal. These considerations motivate us to use enumeration values in all metaprograms throughout this book.
|
17.3 A Second Example: Computing the Square Root
Lets look at a slightly more complicated example: a metaprogram that computes the square root of a given value N
. The metaprogram looks as follows (explanation of the technique follows):
// meta/sqrt1.hpp
#ifndef SQRT_HPP
#define SQRT_HPP
// primary template to compute sqrt(N)
template <int N, int LO=1, int HI=N>
class Sqrt {
public:
// compute the midpoint, rounded up
enum { mid = (LO+HI+1)/2 };
// search a not too large value in a halved interval
enum { result = (N<mid*mid) ? Sqrt<N,LO,mid-1>::result
: Sqrt<N,mid,HI>::result };
};
// partial specialization for the case when LO equals HI
template<int N, int M>
class Sqrt<N,M,M> {
public:
enum { result=M};
};
#endif // SQRT_HPP
The first template is the general recursive computation that is invoked with the template parameter N (the value for which to compute the square root) and two other optional parameters. The latter represent the minimum and maximum values the result can have. If the template is called with only one argument, we know that the square root is at least one and at most the value itself.
Our recursion then proceeds using a binary search technique (often called method of bisection in this context). Inside the template, we compute whether result is in the first or the second half of the range between LO and HI. This case differentiation is done using the conditional operator ? :. If mid2 is greater than N, we continue the search in the first half. If mid2 is less than or equal to N, we use the same template for the second half again.
The specialization that ends the recursive process is invoked when LO and HI have the same value M, which is our final result.
Again, let's look at the details of a simple program that uses this metaprogram:
// meta/sqrt1.cpp
#include <iostream>
#include "sqrt1.hpp"
int main()
{
std::cout << "Sqrt<16>::result = " << Sqrt<16>::result
<< '\n';
std::cout << "Sqrt<25>::result = " << Sqrt<25>::result
<< '\n';
std::cout << "Sqrt<42>::result = " <<Sqrt<42>::result
<< '\n';
std::cout << "Sqrt<1>::result = " << Sqrt<1>::result
<< '\n';
}
The expression
Sqrt<16>::result
is expanded to
Sqrt<16,1,16>::result
Inside the template, the metaprogram computes Sqrt<16,1,16>::result as follows:
mid = (1+16+1)/2
= 9
result = (16<9*9) ? Sqrt<16,1,8>::result
: Sqrt<16,9,16>::result
= (16<81) ? Sqrt<16,1,8>::result
: Sqrt<16,9,16>::result
= Sqrt<16,1,8>::result
Thus, the result is computed as Sqrt<16,1,8>::result, which is expanded as follows:
mid = (1+8+1)/2
= 5
result = (16<5*5) ? Sqrt<16,1,4>::result
: Sqrt<16,5,8>::result
= (16<25) ? Sqrt<16,1,4>::result
: Sqrt<16,5,8>::result
= Sqrt<16,1,4>::result
And similarly Sqrt<16,1,4>::result is decomposed as follows:
mid = (1+4+1)/2
= 3
result = (16<3*3) ? Sqrt<16,1,2>::result
: Sqrt<16,3,4>::result
= (16<9) ? Sqrt<16,1,2>::result
: Sqrt<16,3,4>::result
= Sqrt<16,3,4>::result
Finally, Sqrt<16,3,4>::result results in the following:
mid = (3+4+1)/2
= 4
result = (16<4*4) ? Sqrt<16,3,3>::result
: Sqrt<16,4,4>::result
= (16<16) ? Sqrt<16,3,3>::result
: Sqrt<16,4,4>::result
= Sqrt<16,4,4>::result
and Sqrt<16,4,4>::result ends the recursive process because it matches the explicit specialization that catches equal high and low bounds. The final result is therefore as follows:
result = 4
Tracking All Instantiations
In the preceding example, we followed the significant instantiations that compute the square root of 16. However, when a compiler evaluates the expression
(16<=8*8) ? Sqrt<16,1,8>::result
: Sqrt<16,9,16>::result
it not only instantiates the templates in the positive branch, but also those in the negative branch (Sqrt<16,9,16>). Furthermore, because the code attempts to access a member of the resulting class type using the :: operator, all the members inside that class type are also instantiated. This means that the full instantiation of Sqrt<16,9,16> results in the full instantiation of Sqrt<16,9,12> and Sqrt<16,13,16>. When the whole process is examined in detail, we find that dozens of instantiations end up being generated. The total number is almost twice the value of N.
This is unfortunate because template instantiation is a fairly expensive process for most compilers, particularly with respect to memory consumption. Fortunately, there are techniques to reduce this explosion in the number of instantiations. We use specializations to select the result of computation instead of using the condition operator ?:. To illustrate this, we rewrite our Sqrt metaprogram as follows:
// meta/sqrt2.hpp
#include "ifthenelse.hpp"
// primary template for main recursive step
template<int N, int LO=1, int HI=N>
class Sqrt {
public:
// compute the midpoint, rounded up
enum { mid = (LO+HI+1)/2 };
// search a not too large value in a halved interval
typedef typename IfThenElse<(N<mid*mid),
Sqrt<N,LO,mid-1>,
Sqrt<N,mid,HI> >::ResultT
SubT;
enum { result = SubT::result };
};
// partial specialization for end of recursion criterion
template<int N, int S>
class Sqrt<N, S, S> {
public:
enum { result = S };
};
The key change here is the use of the IfThenElse template, which was introduced in Section 15.2.4 on page 272:
// meta/ifthenelse.hpp
#ifndef IFTHENELSE_HPP
#define IFTHENELSE_HPP
// primary template: yield second or third argument depending on first argument
template<bool C, typename Ta, typename Tb>
class IfThenElse;
// partial specialization: true yields second argument
template<typename Ta, typename Tb>
class IfThenElse<true, Ta, Tb> {
public:
typedef Ta ResultT;
};
// partial specialization: false yields third argument
template<typename Ta, typename Tb>
class IfThenElse<false, Ta, Tb> {
public:
typedef Tb ResultT;
};
#endif // IFTHENELSE_HPP
Remember, the IfThenElse template is a device that selects between two types based on a given Boolean constant. If the constant is true, the first type is typedefed to ResultT; otherwise, ResultT stands for the second type. At this point it is important to remember that defining a typedef for a class template instance does not cause a C++ compiler to instantiate the body of that instance. Therefore, when we write
typedef typename IfThenElse<(N<mid*mid),
Sqrt<N,LO,mid-1>,
Sqrt<N,mid,HI> >::ResultT
SubT;
neither Sqrt<N,LO,mid-1> nor Sqrt<N,mid,HI> is fully instantiated. Whichever of these two types ends up being a synonym for SubT is fully instantiated when looking up SubT::result. In contrast to our first approach, this strategy leads to a number of instantiations that is proportional to log2(N): a very significant reduction in the cost of metaprogramming when N gets moderately large.

|
17.4 Using Induction Variables
You may argue that the way the metaprogram is written in the previous example looks rather complicated. And you may wonder whether you have learned something you can use whenever you have a problem to solve by a metaprogram. So, let's look for a more "naive" and maybe "more iterative" implementation of a metaprogram that computes the square root.
A "naive iterative algorithm" can be formulated as follows: To compute the square root of a given value N, we write a loop in which a variable I iterates from one to N until its square is equal to or greater than N. This value I is our square root of N. If we formulate this problem in ordinary C++, it looks as follows:
int I;
for (I=1; I*I<N; ++I) {
;
}
// I now contains the square root of N
However, as a metaprogram we have to formulate this loop in a recursive way, and we need an end criterion to end the recursion. As a result, an implementation of this loop as a metaprogram looks as follows:
// meta/sqrt3.hpp
#ifndef SQRT_HPP
#define SQRT_HPP
// primary template to compute sqrt(N) via iteration
template <int N, int I=1>
class Sqrt {
public:
enum { result = (I*I<N) ? Sqrt<N,I+1>::result
: I };
};
// partial specialization to end the iteration
template<int N>
class Sqrt<N,N> {
public:
enum { result = N };
};
#endif // SQRT_HPP
We loop by "iterating" I over Sqrt<N,I>. As long as I*I<N yields true, we use the result of the next iteration Sqrt<N,I+1>::result as result. Otherwise I is our result.
For example, if we evaluate Sqrt<16> this gets expanded to Sqrt<16,1>. Thus, we start an iteration with one as a value of the so-called induction variable I. Now, as long as I2 (that is I*I) is less than N, we use the next iteration value by computing Sqrt<N,I+1>::result. When I2 is equal to or greater than N we know that I is the result.
You may wonder why we need a template specialization to end the recursion because the first template always, sooner or later, finds I as the result, which seems to end the recursion. Again, this is the effect of the instantiation of both branches of operator ?:, which was discussed in the previous section. Thus, the compiler computes the result of Sqrt<4> by instantiating as follows:
Step 1:
result = (1*1<4) ? Sqrt<4,2>::result
: 1 Step 2:
result = (1*1<4) ? (2*2<4) ? Sqrt<4,3>::result
: 2
: 1 Step 3:
result = (1*1<4) ? (2*2<4) ? (3*3<4) ? Sqrt<4,4>::result
: 3
: 2
: 1 Step 4:
result = (1*1<4) ? (2*2<4) ? (3*3<4) ? 4
: 3
: 2
: 1
Although we find the result in step 2, the compiler instantiates until we find a step that ends the recursion with a specialization. Without the specialization, the compiler would continue to instantiate until internal compiler limits are reached.
Again, the application of the IfThenElse template solves the problem:
// meta/sqrt4.hpp
#ifndef SQRT_HPP
#define SQRT_HPP
#include "ifthenelse.hpp"
// template to yield template argument as result
template<int N>
class Value {
public:
enum { result = N };
};
// template to compute sqrt(N) via iteration
template <int N, int I=1>
class Sqrt {
public:
// instantiate next step or result type as branch
typedef typename IfThenElse<(I*I<N),
Sqrt<N,I+1>,
Value<I>
>::ResultT
SubT;
// use the result of branch type
enum { result = SubT::result };
};
#endif // SQRT_HPP
Instead of the end criterion we use a Value<> template that returns the value of the template argument as result.
Again, using IfThenElse<> leads to a number of instantiations that is proportional to log
2(N) instead of N. This is a very significant reduction in the cost of metaprogramming. And for compilers with template instantiation limits, this means that you can evaluate the square root of much larger values. If your compiler supports up to 64 nested instantiations, for example, you can process the square root of up to 4096 (instead of up to 64).
The output of the "iterative" Sqrt templates is as follows:
Sqrt<16>::result = 4
Sqrt<25>::result = 5
Sqrt<42>::result = 7
Sqrt<1>::result = 1
Note that this implementation produces the integer square root rounded up for simplicity (the square root of 42 is produced as 7 instead of 6).

|
17.5 Computational Completeness
The Pow3<> and Sqrt<> examples show that a template metaprogram can contain:
State variables: the template parameters Loop constructs: through recursion Path selection: by using conditional expressions or specializations Integer arithmetic
If there are no limits to the amount of recursive instantiations and the amount of state variables that are allowed, it can be shown that this is sufficient to compute anything that is computable. However, it may not be convenient to do so using templates. Furthermore, template instantiation typically requires substantial compiler resources, and extensive recursive instantiation quickly slows down a compiler or even exhausts the resources available. The C++ standard recommends but does not mandate that 17 levels of recursive instantiations be allowed as a minimum. Intensive template metaprogramming easily exhausts such a limit.
Hence, in practice, template metaprograms should be used sparingly. The are a few situations, however, when they are irreplaceable as a tool to implement convenient templates. In particular, they can sometimes be hidden in the innards of more conventional templates to squeeze more performance out of critical algorithm implementations.
|
17.6 Recursive Instantiation versus Recursive Template Arguments
Consider the following recursive template:
template<typename T, typename U>
struct Doublify {};
template<int N>
struct Trouble {
typedef Doublify<typename Trouble<N-1>::LongType,
typename Trouble<N-1>::LongType> LongType;
};
template<>
struct Trouble<0> {
typedef double LongType;
};
Trouble<10>::LongType ouch;
The use of Trouble<10>::LongType not only triggers the recursive instantiation of Trouble<9>, Trouble<8>, …, Trouble<0>, but it also instantiates Doublify over increasingly complex types. Indeed, Table 17.1 illustrates how quickly it grows.
As can be seen from Table 17.1, the complexity of the type description of the expression Trouble<N>::LongType grows exponentially with N. In general, such a situation stresses a C++ compiler even more than recursive instantiations that do not involve recursive template arguments. One of the problems here is that a compiler keeps a representation of the mangled name for the type. This mangled name encodes the exact template specialization in some way, and early C++ implementations used an encoding that is roughly proportional to the length of the template-id. These compilers then used well over 10,000 characters for Trouble<10>::LongType.
Newer C++ implementations take into account the fact that nested template-ids are fairly common in modern C++ programs and use clever compression techniques to reduce considerably the growth
Table 17.1. Growth of Trouble<N>::LongType
Trouble<0>::LongType
Trouble<1>::LongType
Trouble<2>::LongType
Trouble<3>::LongType |
double
Doublify<double,double>
Doublify<Doublify<double,double>,
Doublify<double,double> >
Doublify<Doublify<Doublify<double,double>,
Doublify<double,double> >,
<Doublify<double,double>,
Doublify<double,double> > > |
in name encoding (for example, a few hundred characters for Trouble<10>::LongType). Still, all other things being equal, it is probably preferable to organize recursive instantiation in such a way that template arguments need not also be nested recursively.
|
17.7 Using Metaprograms to Unroll Loops
One of the first practical applications of metaprogramming was the unrolling of loops for numeric computations, which is shown here as a complete example.
Numeric applications often have to process n-dimensional arrays or mathematical vectors. One typical operation is the computation of the so-called dot product. The dot product of two mathematical vectors a and b is the sum of all products of corresponding elements in both vectors. For example, if each vectors has three elements, the result is
a[0]*b[0] + a[1]*b[1] + a[2]*b[2]
A mathematical library typically provides a function to compute such a dot product. Consider the following straightforward implementation:
// meta/loop1.hpp
#ifndef LOOP1_HPP
#define LOOP1_HPP
template <typename T>
inline T dot_product (int dim, T* a, T* b)
{
T result = 0;
for (int i=0; i<dim; ++i) {
result += a[i]*b[i];
}
return result;
}
#endif // LOOP1_HPP
When we call this function as follows
// meta/loop1.cpp
#include <iostream>
#include "loop1.hpp"
int main()
{
int a[3] = { 1, 2, 3 };
int b[3] = { 5, 6, 7 };
std::cout << "dot_product(3,a,b) = " << dot_product(3,a,b)
<< '\n';
std::cout << "dot_product(3,a,a) = " << dot_product(3,a,a)
<< '\n';
}
we get the following result:
dot_product(3,a,b) = 38
dot_product(3,a,a) = 14
This is correct, but it takes too long for serious high-performance applications. Even declaring the function inline is often not sufficient to attain optimal performance.
The problem is that compilers usually optimize loops for many iterations, which is counterproductive in this case. Simply expanding the loop to
a[0]*b[0] + a[1]*b[1] + a[2]*b[2]
would be a lot better.
Of course, this performance doesn't matter if we compute only some dot products from time to time. But, if we use this library component to perform millions of dot product computations, the differences become significant.
Of course, we could write the computation directly instead of calling dot_product(), or we could provide special functions for dot product computations with only a few dimensions, but this is tedious. Template metaprogramming solves this issue for us: We "program" to unroll the loops. Here is the metaprogram:
// meta/loop2.hpp
#ifndef LOOP2_HPP
#define LOOP2_HPP
// primary template
template <int DIM, typename T>
class DotProduct {
public:
static T result (T* a, T* b) {
return *a * *b + DotProduct<DIM-1,T>::result(a+1,b+1);
}
};
// partial specialization as end criteria
template <typename T>
class DotProduct<1,T> {
public:
static T result (T* a, T* b) {
return *a * *b;
}
};
// convenience function
template <int DIM, typename T>
inline T dot_product (T* a, T* b)
{
return DotProduct<DIM,T>::result(a,b);
}
#endif // LOOP2_HPP
Now, by changing your application program only slightly, you can get the same result:
// meta/loop2.cpp
#include <iostream>
#include "loop2.hpp"
int main()
{
int a[3] = { 1, 2, 3};
int b[3] = { 5, 6, 7};
std::cout << "dot_product<3>(a,b) = " << dot_product<3>(a,b)
<< '\n';
std::cout << "dot_product<3>(a,a) = " << dot_product<3>(a,a)
<< '\n';
}
Instead of writing
dot_product(3,a,b)
we write
dot_product<3>(a,b)
This expression instantiates a convenience function template that translates the call into
DotProduct<3,int>::result(a,b)
And this is the start of the metaprogram.
Inside the metaprogram the result is the product of the first elements of a and b plus the result of the dot product of the remaining dimensions of the vectors starting with their next elements:
template <int DIM, typename T>
class DotProduct {
public:
static T result (T* a, T* b) {
return *a * *b + DotProduct<DIM-1,T>::result(a+1,b+1);
}
};
The end criterion is the case of a one-dimensional vector:
template <typename T>
class DotProduct<1,T> {
public:
static T result (T* a, T* b) {
return *a * *b;
}
};
Thus, for
dot_product<3>(a,b)
the instantiation process computes the following:
DotProduct<3,int>::result(a,b)
= *a * *b + DotProduct<2,int>::result(a+1,b+1)
= *a * *b + *(a+1) * *(b+1) + DotProduct<1,int>::result(a+2,b+2)
= *a * *b + *(a+1) * *(b+1) + *(a+2) * *(b+2)
Note that this way of programming requires that the number of dimensions is known at compile time, which is often (but not always) the case.
Libraries, such as Blitz++ (see [Blitz++]), the MTL library (see [MTL]), and POOMA (see [POOMA]), use these kinds of metaprograms to provide fast routines for numeric linear algebra. Such metaprograms often do a better job than optimizers because they can integrate higher-level knowledge into the computations.
The industrial-strength implementation of such libraries involves many more details than the template-related issues we present here. Indeed, reckless unrolling does not always lead to optimal running times. However, these additional engineering considerations fall outside the scope of our text.

|
17.8 Afternotes
As mentioned earlier, the earliest documented example of a metaprogram was by Erwin Unruh, then representing Siemens on the C++ standardization committee. He noted the computational completeness of the template instantiation process and demonstrated his point by developing the first metaprogram. He used the Metaware compiler and coaxed it into issuing error messages that would contain successive prime numbers. Here is the code that was circulated at a C++ committee meeting in 1994 (modified so that it now compiles on standard conforming compilers)
:
// meta/unruh.cpp
// prime number computation by Erwin Unruh
template <int p, int i>
class is_prime {
public:
enum { prim = (p==2) || (p%i) && is_prime<(i>2?p:0),i-1>::prim
};
};
template<>
class is_prime<0,0> {
public:
enum {prim=1};
};
template<>
class is_prime<0,1> {
public:
enum {prim=1};
};
template <int i>
class D {
public:
D(void*);
};
template <int i>
class Prime_print { // primary template for loop to print prime numbers
public:
Prime_print<i-1> a;
enum { prim = is_prime<i,i-1>::prim
};
void f() {
D<i> d = prim ? 1 : 0;
a.f();
}
};
template<>
class Prime_print<1> { // full specialization to end the loop
public:
enum {prim=0};
void f() {
D<1> d = prim ? 1 : 0;
};
};
#ifndef LAST
#define LAST 18
#endif
int main()
{
Prime_print<LAST> a;
a.f();
}
If you compile this program, the compiler will print error messages when in Prime_print::f() the initialization of d fails. This happens when the initial value is 1 because there is only a constructor for void*, and only 0 has a valid conversion to void*. For example, on one compiler we get (among other messages) the following errors:
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<17>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<13>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<11>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<7>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<5>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<3>' requested
unruh.cpp:36: conversion from 'int' to non-scalar type 'D<2>' requested
The concept of C++ template metaprogramming as a serious programming tool was first made popular (and somewhat formalized) by Todd Veldhuizen in his paper Using C++ Template Metaprograms (see [VeldhuizenMeta95]). Todd's work on Blitz++ (a numeric array library for C++, see [Blitz++]) also introduced many refinements and extensions to the metaprogramming (and to expression template techniques, introduced in the next chapter).

|
Chapter 18. Expression Templates
In this chapter we explore a template programming technique called expression templates. It was originally invented in support of numeric array classes, and that is also the context in which we introduce it here.
A numeric array class supports numeric operations on whole array objects. For example, it is possible to add two arrays, and the result contains elements that are the sums of the corresponding values in the argument arrays. Similarly, a whole array can be multiplied by a scalar, meaning that each element of the array is scaled. Naturally, it is desirable to keep the operator notation that is so familiar for built-in scalar types:
Array<double> x(1000), y(1000);
…
x = 1.2*x + x*y;
For the serious number cruncher it is crucial that such expressions be evaluated as efficiently as can be expected from the platform on which the code is run. Achieving this with the compact operator notation of this example is no trivial task, but expression templates will come to our rescue.
Expression templates are reminiscent of template metaprogramming. In part this is due to the fact that expression templates rely on sometimes deeply nested template instantiations, which are not unlike the recursive instantiations encountered in template metaprograms. The fact that both techniques were originally developed to support high-performance (see our example using templates to unroll loops on page 314) array operations probably also contributes to a sense that they are related. Certainly the techniques are complementary. For example, metaprogramming is convenient for small, fixed-size array whereas expression templates are very effective for operations on medium-to-large arrays sized at run time.

|
18.1 Temporaries and Split Loops
To motivate expression templates, let's start with a straightforward (or maybe "naive") approach to implement templates that enable numeric array operations. A basic array template might look as follows (SArray stands for simple array):
// exprtmpl/sarray1.hpp
#include <stddef.h>
#include <cassert>
template<typename T>
class SArray {
public:
// create array with initial size
explicit SArray (size_t s)
: storage(new T[s]), storage_size(s) {
init();
}
// copy constructor
SArray (SArray<T> const& orig)
: storage(new T[orig.size()]), storage_size(orig.size()) {
copy(orig);
}
// destructor: free memory
~SArray() {
delete[] storage;
}
// assignment operator
SArray<T>& operator= (SArray<T> const& orig) {
if (&orig!=this) {
copy(orig);
}
return *this;
}
// return size
size_t size() const {
return storage_size;
}
// index operator for constants and variables
T operator[] (size_t idx) const {
return storage[idx];
}
T& operator[] (size_t idx) {
return storage[idx];
}
protected:
// init values with default constructor
void init() {
for (size_t idx = 0; idx<size(); ++idx) {
storage[idx] = T();
}
}
// copy values of another array
void copy (SArray<T> const& orig) {
assert(size()==orig.size());
for (size_t idx = 0; idx<size(); ++idx) {
storage[idx] = orig.storage[idx];
}
}
private:
T* storage; // storage of the elements
size_t storage_size; // number of elements
};
The numeric operators can be coded as follows:
// exprtmpl/sarrayops1.hpp
// addition of two SArrays
template<typename T>
SArray<T> operator+ (SArray<T> const& a, SArray<T> const& b)
{
SArray<T> result(a.size());
for (size_t k = 0; k<a.size(); ++k) {
result[k] = a[k]+b[k];
}
return result;
}
// multiplication of two SArrays
template<typename T>
SArray<T> operator* (SArray<T> const& a, SArray<T> const& b)
{
SArray<T> result(a.size());
for (size_t k = 0; k<a.size(); ++k) {
result[k] = a[k]*b[k];
}
return result;
}
// multiplication of scalar and SArray
template<typename T>
SArray<T> operator* (T const& s, SArray<T> const& a)
{
SArray<T> result(a.size());
for (size_t k = 0; k<a.size(); ++k) {
result[k] = s*a[k];
}
return result;
}
// multiplication of SArray and scalar
// addition of scalar and SArray
// addition of SArray and scalar
…
Many other versions of these and other operators can be written, but these suffice to allow our example expression:
// exprtmpl/sarray1.cpp
#include "sarray1.hpp"
#include "sarrayops1.hpp"
int main()
{
SArray<double> x(1000), y(1000);
…
x = 1.2*x + x*y;
}
This implementation turns out to be very inefficient for two reasons:
Every application of an operator (except assignment) creates at least one temporary array (that is, at least three temporary arrays of size 1,000 each in our example, assuming a compiler performs all the allowable temporary copy eliminations). Every application of an operator requires additional traversals of the argument and result arrays (approximately 6,000 doubles are read, and approximately 4,000 doubles are written in our example, assuming only three temporary SArray objects are generated).
What happens concretely is a sequence of loops that operates with temporaries:
tmp1 = 1.2*x; // loop of 1,000 operations
// plus creation and destruction of tmp1
tmp2 = x*y // loop of 1,000 operations
// plus creation and destruction of tmp2
tmp3 = tmp1+tmp2; // loop of 1,000 operations
// plus creation and destruction of tmp3
x = tmp3; // 1,000 read operations and 1,000 write operations
The creation of unneeded temporaries often dominates the time needed for operations on small arrays unless special fast allocators are used. For truly large arrays, temporaries are totally unacceptable because there is no storage to hold them. (Challenging numeric simulations often try to use all the available memory for more realistic results. If the memory is used to hold unneeded temporaries instead, the quality of the simulation will suffer.)
Early implementations of numeric array libraries faced this problem and encouraged users to use computed assignments (such as +=, *=, and so forth) instead. The advantage of these assignments is that both the argument and the destination are provided by the caller, and hence no temporaries are needed. For example, we could add SArray members as follows:
// exprtmpl/sarrayops2.hpp
// additive assignment of SArray
template<class T>
SArray<T>& SArray<T>::operator+= (SArray<T> const& b)
{
for (size_t k = 0; k<size(); ++k) {
(*this)[k] += b[k];
}
return *this;
}
// multiplicative assignment of SArray
template<class T>
SArray<T>& SArray<T>::operator*= (SArray<T> const& b)
{
for (size_t k = 0; k<size(); ++k) {
(*this)[k] *= b[k];
}
return *this;
}
// multiplicative assignment of scalar
template<class T>
SArray<T>& SArray<T>::operator*= (T const& s)
{
for (size_t k = 0; k<size(); ++k) {
(*this)[k] *= s;
}
return *this;
}
With operators such as these, our example computation could be rewritten as
// exprtmpl/sarray2.cpp
#include "sarray2.hpp"
#include "sarrayops1.hpp"
#include "sarrayops2.hpp"
int main()
{
SArray<double> x(1000), y(1000);
…
// process x = 1.2*x + x*y
SArray<double> tmp(x);
tmp *= y;
x *= 1.2;
x += tmp;
}
Clearly, the technique using computed assignments still falls short:
The notation has become clumsy. We are still left with an unneeded temporary tmp. The loop is split over multiple operations, requiring a total of approximately 6,000 double elements to be read from memory and 4,000 doubles to be written to memory.
What we really want is one "ideal loop" that processes the whole expression for each index:
int main()
{
SArray<double> x(1000), y(1000);
…
for (int idx = 0; idx<x.size(); ++idx) {
x[idx] = 1.2*x[idx] + x[idx]*y[idx];
}
}
Now we need no temporary array and we have only two memory reads (x[idx] and y[idx]) and one memory write (x[k]) per iteration. As a result, the manual loop requires only approximately 2,000 memory reads and 1,000 memory writes.
Given that on modern, high-performance computer architectures memory bandwidth is the limiting factor for the speed of these sorts of array operations, it is not surprising that in practice the performance of the simple operator overloading approaches shown here is one or two orders of magnitude slower than the manually coded loop. However, we would like to get this performance without the cumbersome and error-prone effort of writing these loops by hand or using a clumsy notation.
|
18.2 Encoding Expressions in Template Arguments
The key to resolving our problem is not to attempt to evaluate part of an expression until the whole expression has been seen (in our example, until the assignment operator is invoked). Thus, before the evaluation we must record which operations are being applied to which objects. The operations are determined at compile time and can therefore be encoded in template arguments.
For our example expression
1.2*x + x*y;
this means that the result of 1.2*x is not a new array but an object that represents each value of x multiplied by 1.2. Similarly, x*y must yield each element of x multiplied by each corresponding element of y. Finally, when we need the values of the resulting array, we do the computation that we stored for later evaluation.
Let's look at a concrete implementation. With this implementation we transform the written expression
1.2*x + x*y;
into an object with the following type:
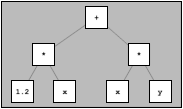
A_Add< A_Mult<A_Scalar<double>,Array<double> >,
A_Mult<Array<double>,Array<double> > >
We combine a new fundamental Array class template with class templates A_Scalar, A_Add, and A_Mult. You may recognize a prefix representation for the syntax tree corresponding to this expression (see Figure 18.1). This nested template-id represents the operations involved and the types of the objects to which the operations should be applied. A_Scalar is presented later but is essentially just a placeholder for a scalar in an array expression.
18.2.1 Operands of the Expression Templates
To complete the representation of the expression, we must store references to the arguments in each of the A_Add and A_Mult objects and record the value of the scalar in the A_Scalar object (or a reference thereto). Here are possible definitions for the corresponding operands:
// exprtmpl/exprops1.hpp
#include <stddef.h>
#include <cassert>
// include helper class traits template to select wether to refer to an
// ''expression template node'' either ''by value'' or ''by reference.''
#include "exprops1a.hpp"
// class for objects that represent the addition of two operands
template <typename T, typename OP1, typename OP2>
class A_Add {
private:
typename A_Traits<OP1>::ExprRef op1; // first operand
typename A_Traits<OP2>::ExprRef op2; // second operand
public:
// constructor initializes references to operands
A_Add (OP1 const& a, OP2 const& b)
: op1(a), op2(b) {
}
// compute sum when value requested
T operator[] (size_t idx) const {
return op1[idx] + op2[idx];
}
// size is maximum size
size_t size() const {
assert (op1.size()==0 || op2.size()==0
|| op1.size()==op2.size());
return op1.size()!=0 ? op1.size() : op2.size();
}
};
// class for objects that represent the multiplication of two operands
template <typename T, typename OP1, typename OP2>
class A_Mult {
private:
typename A_Traits<OP1>::ExprRef op1; // first operand
typename A_Traits<OP2>::ExprRef op2; // second operand
public:
// constructor initializes references to operands
A_Mult (OP1 const& a, OP2 const& b)
: op1(a), op2(b) {
}
// compute product when value requested
T operator[] (size_t idx) const {
return op1[idx] * op2[idx];
}
// size is maximum size
size_t size() const {
assert (op1.size()==0 || op2.size()==0
|| op1.size()==op2.size());
return op1.size()!=0 ? op1.size() : op2.size();
}
};
As you can see, we added subscripting and size-querying operations that allow us to compute the size and the values of the elements for the array resulting from the operations represented by the subtree of "nodes" rooted at the given object.
For operations involving arrays only, the size of the result is the size of either operand. However, for operations involving both an array and a scalar, the size of the result is the size of the array operand. To distinguish array operands from scalar operands, we define a size of zero for scalars. The A_Scalar template is therefore defined as follows:
// exprtmpl/exprscalar.hpp
// class for objects that represent scalars
template <typename T>
class A_Scalar {
private:
T const& s; // value of the scalar
public:
// constructor initializes value
A_Scalar (T const& v)
: s(v) {
}
// for index operations the scalar is the value of each element
T operator[] (size_t) const {
return s;
}
// scalars have zero as size
size_t size() const {
return 0;
};
};
Note that scalars also provide an index operator. Inside the expression, they represent an array with the same scalar value for each index.
You probably saw that the operator classes used a helper class A_Traits to define the members for the operands:
typename A_Traits<OP1>::ExprRef op1; // first operand
typename A_Traits<OP2>::ExprRef op2; // second operand
This is necessary because of the following: In general, we can declare them to be references because most temporary nodes are bound in the top-level expression and therefore live until the end of the evaluation of that complete expression. The one exception are the A_Scalar nodes. They are bound within the operator functions and might not live until the end of the evaluation of the complete expression. Thus, to avoid that the members refer to scalars that don't exist anymore, for scalars the operands have to get copied "by value." In other words, we need members that are
constant references in general:
OP1 const& op1; // refer to first operand by reference
OP2 const& op2; // refer to second operand by reference but ordinary values for scalars:
OP1 op1; // refer to first operand by value
OP2 op2; // refer to second operand by value
This is a perfect application of traits classes. The traits class defines a type to be a constant reference in general, but an ordinary value for scalars:
// exprtmpl/exprops1a.hpp
/* helper traits class to select how to refer to an ''expression template node''
* - in general: by reference
* - for scalars: by value
*/
template <typename T> class A_Scalar;
// primary template
template <typename T>
class A_Traits {
public:
typedef T const& ExprRef; // type to refer to is constant reference
};
// partial specialization for scalars
template <typename T>
class A_Traits<A_Scalar<T> > {
public:
typedef A_Scalar<T> ExprRef; // type to refer to is ordinary value
};
Note that since A_Scalar objects refer to scalars in the top-level expression, those scalars can use reference types.
18.2.2 The Array Type
With our ability to encode expressions using lightweight expression templates, we must now create an Array type that controls actual storage and that knows about the expression templates. However, it is also useful for engineering purposes to keep as similar as possible the interface for a real array with storage and one for a representation of an expression that results in an array. To this end, we declare the Array template as follows:
template <typename T, typename Rep = SArray<T> >
class Array;
The type Rep can be SArray if Array is a real array of storage,
or it can be the nested template-id such as A_Add or A_Mult that encodes an expression. Either way we are handling Array instantiations, which considerably simplify our later dealings. In fact, even the definition of the Array template needs no specializations to distinguish the two cases, although some of the members cannot be instantiated for types like A_Mult substituted for Rep.
Here is the definition. The functionality is limited roughly to what was provided by our SArray template, although once the code is understood, it is not hard to add to that functionality:
// exprtmpl/exprarray.hpp
#include <stddef.h>
#include <cassert>
#include "sarray1.hpp"
template <typename T, typename Rep = SArray<T> >
class Array {
private:
Rep expr_rep; // (access to) the data of the array
public:
// create array with initial size
explicit Array (size_t s)
: expr_rep(s) {
}
// create array from possible representation
Array (Rep const& rb)
: expr_rep(rb) {
}
// assignment operator for same type
Array& operator= (Array const& b) {
assert(size()==b.size());
for (size_t idx = 0; idx<b.size(); ++idx) {
expr_rep[idx] = b[idx];
}
return *this;
}
// assignment operator for arrays of different type
template<typename T2, typename Rep2>
Array& operator= (Array<T2, Rep2> const& b) {
assert(size()==b.size());
for (size_t idx = 0; idx<b.size(); ++idx) {
expr_rep[idx] = b[idx];
}
return *this;
}
// size is size of represented data
size_t size() const {
return expr_rep.size();
}
// index operator for constants and variables
T operator[] (size_t idx) const {
assert(idx<size());
return expr_rep[idx];
}
T& operator[] (size_t idx) {
assert(idx<size());
return expr_rep[idx];
}
// return what the array currently represents
Rep const& rep() const {
return expr_rep;
}
Rep& rep() {
return expr_rep;
}
};
As you can see, many operations are simply forwarded to the underlying Rep object. However, when copying another array, we must take into account the possibility that the other array is really built on an expression template. Thus, we parameterize these copy operations in terms of the underlying Rep representation.
18.2.3 The Operators
We have most of the machinery in place to have efficient numeric operators for our numeric Array template, except the operators themselves. As implied earlier, these operators only assemble the expression template objectsthey don't actually evaluate the resulting arrays.
For each ordinary binary operator we must implement three versions: array-array, array-scalar, and scalar-array. To be able to compute our initial value we need, for example, the following operators:
// exprtmpl/exprops2.hpp
// addition of two Arrays
template <typename T, typename R1, typename R2>
Array<T,A_Add<T,R1,R2> >
operator+ (Array<T,R1> const& a, Array<T,R2> const& b) {
return Array<T,A_Add<T,R1,R2> >
(A_Add<T,R1,R2>(a.rep(),b.rep()));
}
// multiplication of two Arrays
template <typename T, typename R1, typename R2>
Array<T, A_Mult<T,R1,R2> >
operator* (Array<T,R1> const& a, Array<T,R2> const& b) {
return Array<T,A_Mult<T,R1,R2> >
(A_Mult<T,R1,R2>(a.rep(), b.rep()));
}
// multiplication of scalar and Array
template <typename T, typename R2>
Array<T, A_Mult<T,A_Scalar<T>,R2> >
operator* (T const& s, Array<T,R2> const& b) {
return Array<T,A_Mult<T,A_Scalar<T>,R2> >
(A_Mult<T,A_Scalar<T>,R2>(A_Scalar<T>(s), b.rep()));
}
// multiplication of Array and scalar
// addition of scalar and Array
// addition of Array and scalar
…
The declaration of these operators is somewhat cumbersome (as can be seen from these examples), but the functions really don't do much. For example, the plus operator for two arrays first creates an A_Add<> object that represents the operator and the operands
A_Add<T,R1,R2>(a.rep(),b.rep())
and wraps this object in an Array object so that we can use the result as any other object that represents data of an array:
return Array<T,A_Add<T,R1,R2> > (… );
For scalar multiplication, we use the A_Scalar template to create the A_Mult object
A_Mult<T,A_Scalar<T>,R2>(A_Scalar<T>(s), b.rep())
and wrap again:
return Array<T,A_Mult<T,A_Scalar<T>,R2> > (… );
Other nonmember binary operators are so similar that macros can be used to cover most operators with relatively little source code. Another (smaller) macro could be used for nonmember unary operators.
18.2.4 Review
On first discovery of the expression template idea, the interaction of the various declarations and definitions can be daunting. Hence, a top-down review of what happens with our example code may help crystallize understanding. The code we will analyze is the following (you can find it as part of meta/exprmain.cpp):
int main()
{
Array<double> x(1000), y(1000);
…
x = 1.2*x + x*y;
}
Because the Rep argument is omitted in the definition of x and y, it is set to the default, which is SArray<double>. So, x and y are arrays with "real" storage and not just recordings of operations.
When parsing the expression
1.2*x + x*y
the compiler first applies the leftmost * operation, which is a scalar-array operator. Overload resolution thus selects the scalar-array form of operator*:
template <typename T, typename R2>
Array<T, A_Mult<T,A_Scalar<T>,R2> >
operator* (T const& s, Array<T,R2> const& b) {
return Array<T,A_Mult<T,A_Scalar<T>,R2> >
(A_Mult<T,A_Scalar<T>,R2>(A_Scalar<T>(s), b.rep()));
}
The operand types are double and Array<double, SArray<double> >. Thus, the type of the result is
Array<double, A_Mult<double, A_Scalar<double>, SArray<double> > >
The result value is constructed to reference an A_Scalar<double> object constructed from the double value 1.2 and the SArray<double> representation of the object x.
Next, the second multiplication is evaluated: It is an array-array operation x*y. This time we use the appropriate operator*:
template <typename T, typename R1, typename R2>
Array<T, A_Mult<T,R1,R2> >
operator* (Array<T,R1> const& a, Array<T,R2> const& b) {
return Array<T,A_Mult<T,R1,R2> >
(A_Mult<T,R1,R2>(a.rep(), b.rep()));
}
The operand types are both Array<double, SArray<double> >, so the result type is
Array<double, A_Mult<double, SArray<double>, SArray<double> > >
This time the wrapped A_Mult object refers to two SArray<double> representations: the one of x and the one of y.
Finally, the + operation is evaluated. It is again an array-array operation, and the operand types are the result types that we just deduced. So, we invoke the array-array operator +:
template <typename T, typename R1, typename R2>
Array<T,A_Add<T,R1,R2> >
operator+ (Array<T,R1> const& a, Array<T,R2> const& b) {
return Array<T,A_Add<T,R1,R2> >
(A_Add<T,R1,R2>(a.rep(),b.rep()));
}
T is substituted with double whereas R1 is substituted with
A_Mult<double, A_Scalar<double>, SArray<double> >
and R2 is substituted with
A_Mult<double, SArray<double>, SArray<double> >
Hence, the type of the expression to the right of the assignment token is
Array<double,
A_Add<double,
A_Mult<double, A_Scalar<double>, SArray<double> >,
A_Mult<double, SArray<double>, SArray<double>>>>
This type is matched to the assignment operator template of the Array template:
template <typename T, typename Rep = SArray<T> >
class Array {
public:
…
// assignment operator for arrays of different type
template<typename T2, typename Rep2>
Array& operator= (Array<T2, Rep2> const& b) {
assert(size()==b.size());
for (size_t idx = 0; idx<b.size(); ++idx) {
expr_rep[idx] = b[idx];
}
return *this;
}
…
};
The assignment operator computes each element of the destination x by applying the subscript operator to the representation of the right side, the type of which is
A_Add<double,
A_Mult<double, A_Scalar<double>, SArray<double> >,
A_Mult<double, SArray<double>, SArray<double> > > >
Carefully tracing this subscript operator shows that for a given subscript idx, it computes
(1.2*x[idx]) + (x[idx]*y[idx])
which is exactly what we want.
18.2.5 Expression Templates Assignments
It is not possible to instantiate write operations for an array with a Rep argument that is built on our example A_Mult and A_Add expression templates. (Indeed, it makes no sense to write a+b = c.) However, it is entirely reasonable to write other expression templates for which assignment to the result is possible. For example, indexing with an array of integral values would intuitively correspond to subset selection. In other words, the expression
x[y] = 2*x[y];
should mean the same as
for (size_t idx = 0; idx<y.size(); ++idx) {
x[y[idx]] = 2*x[y[idx]];
}
Enabling this implies that an array built on an expression template behaves like an lvalue (that is, is "writable"). The expression template component for this is not fundamentally different from, say, A_Mult, except that both const and non-const versions of the subscript operators are provided and they return lvalues (references):
// exprtmpl/exprops3.hpp
template<typename T, typename A1, typename A2>
class A_Subscript {
public:
// constructor initializes references to operands
A_Subscript (A1 const & a, A2 const & b)
: a1(a), a2(b) {
}
// process subscription when value requested
T operator[] (size_t idx) const {
return a1[a2[idx]];
}
T& operator[] (size_t idx) {
return a1[a2[idx]];
}
// size is size of inner array
size_t size() const {
return a2.size();
}
private:
A1 const & a1; // reference to first operand
A2 const & a2; // reference to second operand
};
The extended subscript operator with subset semantics that was suggested earlier would require that additional subscript operators be added to the Array template. One of these operators could be defined as follows (a corresponding const version would presumably also be needed):
// exprtmpl/exprops4.hpp
template<typename T, typename R1, typename R2>
Array<T,A_Subscript<T,R1,R2> >
Array<T,R1>::operator[] (Array<T,R2> const & b) {
return Array<T,A_Subscript<T,R1,R2> >
(A_Subscript<T,R1,R2>(a.rep(),b.rep()));
}
|
18.3 Performance and Limitations of Expression Templates
To justify the complexity of the expression template idea, we have already invoked greatly enhanced performance on arraywise operations. As you trace what happens with the expression templates, you'll find that many small inline functions call each other and that many small expression template objects are allocated on the call stack. The optimizer must perform complete inlining and elimination of the small objects to produce code that performs as well as manually coded loops. The latter feat is still rare among C++ compilers at the time of this writing.
The expression templates technique does not resolve all the problematic situations involving numeric operations on arrays. For example, it does not work for matrix-vector multiplications of the form
x = A*x;
where x is a column vector of size n and A is an n-by-n matrix. The problem here is that a temporary must be used because each element of the result can depend on each element of the original x. Unfortunately, the expression template loop updates the first element of x right away and then uses that newly computed element to compute the second element, which is wrong. The slightly different expression
x = A*y;
on the other hand, does not need a temporary if x and y aren't aliases for each other, which implies that a solution would have to know the relationship of the operands at run time. This in turn suggests creating a run-time structure that represents the expression tree instead of encoding the tree in the type of the expression template. This approach was pioneered by the NewMat library of Robert Davies (see [NewMat]). It was known long before expression templates were developed.
Expression templates aren't limited to numeric computations either. An intriguing application, for example, is Jaakko Järvi and Gary Powell's Lambda Library (see [LambdaLib]). This library uses standard library function objects as expression objects. For example, it allows us to write the following:
void lambda_demo (std::vector<long*> & ones) {
std::sort(ones.begin(), ones.end(), *_1 > *_2);
}
This short code excerpt sorts an array in increasing order of the value of what its elements refer to. Without the Lambda library, we'd have to define a simple (but cumbersome) special-purpose functor type. Instead, we can now use simple inline syntax to express the operations we want to apply. In our example, _1 and _2 are placeholders provided by the Lambda library. They correspond to elementary expression objects that are also functors. They can then be used to construct more complex expressions using the techniques developed in this chapter.
|
18.4 Afternotes
Expression templates were developed independently by Todd Veldhuizen and David Vandevoorde (Todd coined the term) at a time when member templates were not yet part of the C++ programming language (and it seemed at the time that they would never be added to C++). This caused some problems in implementing the assignment operator: It could not be parameterized for the expression template. One technique to work around this consisted of introducing in the expression templates a conversion operator to a Copier class parameterized with the expression template but inheriting from a base class that was parameterized only in the element type. This base class then provided a (virtual) copy_to interface to which the assignment operator could refer. Here is a sketch of the mechanism (with the template names used in this chapter):
template<typename T>
class CopierInterface {
public:
virtual void copy_to(Array<T, SArray<T> >&) const;
};
template<typename T, typename X>
class Copier : public CopierBase<T> {
public:
Copier(X const &x): expr(x) {}
virtual void copy_to(Array<T, SArray<T> >&) const {
// implementation of assignment loop
…
}
private:
X const &expr;
};
template<typename T, typename Rep = SArray<T> >
class Array {
public:
// delegated assignment operator
Array<T, Rep>& operator=(CopierBase<T> const &b) {
b.copy_to(rep);
};
…
};
template<typename T, typename A1, typename A2>
class A_mult {
public:
operator Copier<T, A_Mult<T, A1, A2> >();
…
};
This adds another level of complexity and some additional run-time cost to expression templates, but even so the resulting performance benefits were impressive at the time.
The C++ standard library contains a class template valarray that was meant to be used for applications that would justify the techniques used for the Array template developed in this chapter. A precursor of valarray had been designed with the intention that compilers aiming at the market for scientific computation would recognize the array type and use highly optimized internal code for their operations. Such compilers would have "understood" the types in some sense. However, this never happened (in part because the market in question is relatively small and in part because the problem grew in complexity as valarray became a template). Some time after the expression template technique was discovered, one of us (Vandevoorde) submitted to the C++ committee a proposal that turned valarray essentially into the Array template we developed (with many bells and whistles inspired by the existing valarray functionality). The proposal was the first time that the concept of the Rep parameter was documented. Prior to this, the arrays with actual storage and the expression template pseudo-arrays were different templates. When client code introduced a function foo() accepting an arrayfor example,
double foo(Array<double> const&);
calling foo(1.2*x) forced the conversion for the expression template to an array with actual storage, even when the operations applied to that argument did not require a temporary. With expresssion templates embedded in the Rep argument it is possible instead to declare
template<typename R>
double foo(Array<double, R> const&);
and no conversion happens unless one is actually needed.
The valarray proposal came late in the C++ standardization process and practically rewrote all the text regarding valarray in the standard. It was rejected as a result, and instead, a few tweaks were added to the existing text to allow implementations based on expression templates. However, the exploitation of this allowance remains much more cumbersome than what was discussed here. At the time of this writing, no such implementation is known, and standard valarrays are, generally speaking, quite inefficient at performing the operations for which they were designed.
Finally, it is worth observing here that many of the pioneering techniques presented in this chapter, as well as what later became known as the STL,
were all originally implemented on the same compiler: version 4 of the Borland C++ compiler. This was perhaps the first compiler that made template programming widely available to the C++ programming community.

|
Chapter 19. Type Classification
It is sometimes useful to be able to know whether a template parameter is a built-in type, a pointer type, or a class type, and so forth. In the following sections we develop a general-purpose type template that allows us to determine various properties of a given type. As a result we will be able to write code like the following:
if (TypeT<T>::IsPtrT) {
…
}
else if (TypeT<T>::IsClassT) {
…
}
Furthermore, expressions such as TypeT<T>::IsPtrT will be Boolean constants that are valid nontype template arguments. In turn, this allows the construction of more sophisticated and more powerful templates that specialize their behavior on the properties of their type arguments.
|
19.1 Determining Fundamental Types
To start, let's develop a template to determine whether a type is a fundamental type. By default, we assume a type is not fundamental, and we specialize the template for the fundamental cases:
// types/type1.hpp
// primary template: in general T is no fundamental type
template <typename T>
class IsFundaT {
public:
enum{ Yes = 0, No = 1};
};
// macro to specialize for fundamental types
#define MK_FUNDA_TYPE(T) \
template<> class IsFundaT<T> { \
public: \
enum { Yes = 1, No = 0 }; \
};
MK_FUNDA_TYPE(void)
MK_FUNDA_TYPE(bool)
MK_FUNDA_TYPE(char)
MK_FUNDA_TYPE(signed char)
MK_FUNDA_TYPE(unsigned char)
MK_FUNDA_TYPE(wchar_t)
MK_FUNDA_TYPE(signed short)
MK_FUNDA_TYPE(unsigned short)
MK_FUNDA_TYPE(signed int)
MK_FUNDA_TYPE(unsigned int)
MK_FUNDA_TYPE(signed long)
MK_FUNDA_TYPE(unsigned long)
#if LONGLONG_EXISTS
MK_FUNDA_TYPE(signed long long)
MK_FUNDA_TYPE(unsigned long long)
#endif // LONGLONG_EXISTS
MK_FUNDA_TYPE(float)
MK_FUNDA_TYPE(double)
MK_FUNDA_TYPE(long double)
#undef MK_FUNDA_TYPE
The primary template defines the general case. That is, in general, IsFundaT<T
>::Yes will yield 0 (or false):
template <typename T>
class IsFundaT {
public:
enum{ Yes = 0, No = 1 };
};
For each fundamental type a specialization is defined so that IsFundaT<T
>::Yes will yield 1 (or true). This is done by defining a macro that expands the necessary code. For example,
MK_FUNDA_TYPE(bool)
expands to the following:
template<> class IsFundaT<bool> {
public:
enum{ Yes = 1, No = 0 };
};
The following program demonstrates a possible use of this template:
// types/type1test.cpp
#include <iostream>
#include "type1.hpp"
template <typename T>
void test (T const& t)
{
if (IsFundaT<T>::Yes) {
std::cout << "T is fundamental type" << std::endl;
}
else {
std::cout << "T is no fundamental type" << std::endl;
}
}
class MyType {
};
int main()
{
test(7);
test(MyType());
}
It has the following output:
T is fundamental type
T is no fundamental type
In the same way, we can define type functions IsIntegralT and IsFloatingT to identify which of these types are integral scalar types and which are floating-point scalar types.
|
19.2 Determining Compound Types
Compound types are types constructed from other types. Simple compound types include plain types, pointer types, reference types, and even array types. They are constructed from a single base type. Class types and function types are also compound types, but their composition can involve multiple types (for parameters or members). Simple compound types can be classified using partial specialization. We start with a generic definition of a traits class describing compound types other than class types and enumeration types (the latter are treated separately):
// types/type2.hpp
template<typename T>
class CompoundT { // primary template
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = 0, IsPtrMemT = 0 };
typedef T BaseT;
typedef T BottomT;
typedef CompoundT<void> ClassT;
};
The member type BaseT is a synonym for the immediate type on which the template parameter type T builds. BottomT, on the other hand, refers to the ultimate nonpointer, nonreference, and nonarray type on which T is built. For example, if T is int**, then BaseT would be int*, and BottomT would be int. For pointer-to-member types, BaseT is the type of the member, and ClassT is the class to which the member belongs. For example, if T is a pointer-to-member function of type int(X::*)(), then BaseT is the function type int(), and ClassT is X. If T is not a pointer-to-member type, the ClassT is CompoundT<void> (an arbitrary choice; you might prefer a nonclass).
Partial specializations for pointers and references are fairly straightforward:
// types/type3.hpp
template<typename T>
class CompoundT<T&> { // partial specialization for references
public:
enum { IsPtrT = 0, IsRefT = 1, IsArrayT = 0,
IsFuncT = 0, IsPtrMemT = 0 };
typedef T BaseT;
typedef typename CompoundT<T>::BottomT BottomT;
typedef CompoundT<void> ClassT;
};
template<typename T>
class CompoundT<T*> { // partial specialization for pointers
public:
enum { IsPtrT = 1, IsRefT = 0, IsArrayT = 0,
IsFuncT = 0, IsPtrMemT = 0 };
typedef T BaseT;
typedef typename CompoundT<T>::BottomT BottomT;
typedef CompoundT<void> ClassT;
};
Arrays and pointers to members can be treated using the same technique, but it may come as a surprise that the partial specializations involve more template parameters than the primary template:
// types/type4.hpp
#include <stddef.h>
template<typename T, size_t N>
class CompoundT <T[N]> { // partial specialization for arrays
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 1,
IsFuncT = 0, IsPtrMemT = 0 };
typedef T BaseT;
typedef typename CompoundT<T>::BottomT BottomT;
typedef CompoundT<void> ClassT;
};
template<typename T>
class CompoundT <T[]> { // partial specialization for empty arrays
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 1,
IsFuncT = 0, IsPtrMemT = 0 };
typedef T BaseT;
typedef typename CompoundT<T>::BottomT BottomT;
typedef CompoundT<void> ClassT;
};
template<typename T, typename C>
class CompoundT <T C::*> { // partial specialization for pointer-to-members
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = 0, IsPtrMemT = 1 };
typedef T BaseT;
typedef typename CompoundT<T>::BottomT BottomT;
typedef C ClassT;
};
The watchful reader may have noted that the definition of the BottomT member requires the recursive instantiation of the CompoundT template for various types T. The recursion ends when T is no longer a compound type; hence the generic template definition is used (or when T is a function type, as we see later on).
Function types are harder to recognize. In the next section we use fairly advanced template techniques to recognize function types.
|
19.3 Identifying Function Types
The problem with function types is that because of the arbitrary number of parameters, there isn't a finite syntactic construct using template parameters that describes them all. One approach to resolve this problem is to provide partial specializations for functions with a template argument list that is shorter than a chosen limit. The first few such partial specializations can be defined as follows:
// types/type5.hpp
template<typename R>
class CompoundT<R()> {
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = 1, IsPtrMemT = 0 };
typedef R BaseT();
typedef R BottomT();
typedef CompoundT<void> ClassT;
};
template<typename R, typename P1>
class CompoundT<R(P1)> {
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = 1, IsPtrMemT = 0 };
typedef R BaseT(P1);
typedef R BottomT(P1);
typedef CompoundT<void> ClassT;
};
template<typename R, typename P1>
class CompoundT<R(P1, ...)> {
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = 1, IsPtrMemT = 0 };
typedef R BaseT(P1);
typedef R BottomT(P1);
typedef CompoundT<void> ClassT;
};
…
This approach has the advantage that we can create typedef members for each parameter type.
A more general technique uses the SFINAE (substitution-failure-is-not-an-error) principle of Section 8.3.1 on page 106: An overloaded function template can be followed by explicit template arguments that are invalid for some of the templates. This can be combined with the approach used for the classification of enumeration types using overload resolution. The key to exploit SFINAE is to find a type construct that is invalid for function types but not for other types, or vice versa. Because we are already able to recognize various type categories, we can also exclude them from consideration. Therefore, one construct that is useful is the array type. Its elements cannot be void, references, or functions. This inspires the following code:
template<typename T>
class IsFunctionT {
private:
typedef char One;
typedef struct { char a[2]; } Two;
template<typename U> static One test(...);
template<typename U> static Two test(U (*)[1]);
public:
enum { Yes = sizeof(IsFunctionT<T>::test<T>(0)) == 1 };
enum { No = !Yes };
};
With this template definition, IsFunctionT<T>::Yes is nonzero only for types that cannot be types of array elements. The only shortcoming of this observation is that this is not only the case for function types, but it is also the case for reference types and for void types. Fortunately, this is easily remedied by providing partial specialization for reference types and explicit specializations for void types:
template<typename T>
class IsFunctionT<T&> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
template<>
class IsFunctionT<void> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
template<>
class IsFunctionT<void const> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
…
Various alternatives exist. For example, a function type F is also unique in that a reference F& implicitly converts to F* without an user-defined conversion.
These considerations allow us to rewrite the primary CompoundT template as follows:
// types/type6.hpp
template<typename T>
class IsFunctionT {
private:
typedef char One;
typedef struct { char a[2]; } Two;
template<typename U> static One test(...);
template<typename U> static Two test(U (*)[1]);
public:
enum { Yes = sizeof(IsFunctionT<T>::test<T>(0)) == 1 };
enum { No = !Yes };
};
template<typename T>
class IsFunctionT<T&> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
template<>
class IsFunctionT<void> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
template<>
class IsFunctionT<void const> {
public:
enum { Yes = 0 };
enum { No = !Yes };
};
// same for void volatile and void const volatile
…
template<typename T>
class CompoundT { // primary template
public:
enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
IsFuncT = IsFunctionT<T>::Yes,
IsPtrMemT = 0 };
typedef T BaseT;
typedef T BottomT;
typedef CompoundT<void> ClassT;
};
This implementation of the primary template does not exclude the specializations proposed earlier, so that for a limited number of parameters the return types and the parameter types can be accessed.
An interesting historical alternative relies on the fact that at some time in the history of C++,
template<class T>
struct X {
long aligner;
Tm;
};
could declare a member function X::m() instead of a nonstatic data member X::m (this is no longer true in standard C++). On all implementations of that time, X<T> would not be larger than the following X0 type when T was a function type (because nonvirtual member functions don't increase the size of a class in practice):
struct X0 {
long aligner;
};
On the other hand, X<T> would be larger than X0 if T were an object type (the member aligner was required because, for example, an empty class typically has the same size as a class with just a char member).
With all this in place, we can now classify all types, except class types and enumeration types. If a type is not a fundamental type and not one of the types recognized using the CompoundT template, it must be an enumeration or a class type. In the following section, we rely on overload resolution to distinguish between the two.
|
19.4 Enumeration Classification with Overload Resolution
Overload resolution is the process that selects among various functions with a same name based on the types of their arguments. As shown shortly, we can determine the outcome of a case of overload resolution without actually evaluating a function call. This is useful to test whether a particular implicit conversion exists. The implicit conversion that interests us particularly is the conversion from an enumeration type to an integral type: It allows us to identify enumeration types.
Explanations follow the complete implementation of this technique:
// types/type7.hpp
struct SizeOverOne { char c[2]; };
template<typename T,
bool convert_possible = !CompoundT<T>::IsFuncT &&
!CompoundT<T>::IsArrayT>
class ConsumeUDC {
public:
operator T() const;
};
// conversion to function types is not possible
template <typename T>
class ConsumeUDC<T, false> {
};
// conversion to void type is not possible
template <bool convert_possible>
class ConsumeUDC<void, convert_possible> {
};
char enum_check(bool);
char enum_check(char);
char enum_check(signed char);
char enum_check(unsigned char);
char enum_check(wchar_t);
char enum_check(signed short);
char enum_check(unsigned short);
char enum_check(signed int);
char enum_check(unsigned int);
char enum_check(signed long);
char enum_check(unsigned long);
#if LONGLONG_EXISTS
char enum_check(signed long long);
char enum_check(unsigned long long);
#endif // LONGLONG_EXISTS
// avoid accidental conversions from float to int
char enum_check(float);
char enum_check(double);
char enum_check(long double);
SizeOverOne enum_check(...); // catch all
template<typename T>
class IsEnumT {
public:
enum { Yes = IsFundaT<T>::No &&
!CompoundT<T>::IsRefT &&
!CompoundT<T>::IsPtrT &&
!CompoundT<T>::IsPtrMemT &&
sizeof(enum_check(ConsumeUDC<T>()))==1 };
enum { No = !Yes };
};
At the heart of our device is a sizeof expression applied to a function call. It results in the size of the return type of the selected function. Hence, overload selection rules are applied to resolve the call to enum_check(), but no definition of the function is needed because the function is not actually called. In this case, enum_check() returns a char, which has size 1 if the argument is convertible to an integral type. All other types are covered by an ellipsis function, but passing an argument "by ellipsis" is the least desirable from an overload resolution point of view. The return type of the ellipsis version of enum_check() was created specifically to ensure it has a size larger than one byte.
The argument for the call to enum_check() must be created carefully. First, note that we don't actually know how a T can be constructed. Perhaps a special constructor must be called? To resolve this problem, we can declare a function that returns a T and create an argument by calling that function instead. Because we are in a sizeof expression, we don't actually need to define the function. Perhaps more subtle is the fact that overload resolution could select an enum_check() declaration for an integral type if the argument has a class type T, but that class type defines a user-defined conversion (sometimes also called UDC) function to an integral type. This problem is solved by actually forcing a user-defined conversion to T using the ConsumeUDC template. The conversion operator also takes care of creating the argument of type T. The expression for the call to enum_check() is thus analyzed as follows (see Appendix B for a detailed overview of overload resolution):
The original argument is a temporary ConsumeUDC<T> object. If T is a fundamental integral type, the conversion operator is relied on to create a match with an enum_check() that takes type T as its second argument. If T is an enumeration type, the conversion operator is relied on to enable conversion to T, and type promotion is invoked to match an enum_check() that takes an integral type (typically, enum_check(int,int)). If T is a class type with a conversion operator to an integral type, the conversion operator cannot be considered because only one user-defined conversion can be invoked for a match and we would first have to use another such conversion from ConsumeUDC<T> to T. No other type T could be made to match an integral type, so the ellipsis version of enum_check() is selected.
Finally, because we want to identify only enumeration types and not fundamental or pointer types, we use the IsFundaT and CompoundT types developed earlier to exclude those from the set of types that cause IsEnumT<T>::Yes to be nonzero.

|
19.5 Determining Class Types
With all the classification templates described in the previous section, only class types (classes, structs, and unions) remain to be recognized. One approach is to use the SFINAE principle as demonstrated in Section 15.2.2 on page 266.
Another approach is to proceed by elimination: If a type is not a fundamental type, not an enumeration type, and not a compound type, it must be a class type. The following straightforward template implements this idea:
// types/type8.hpp
template<typename T>
class IsClassT {
public:
enum { Yes = IsFundaT<T>::No &&
IsEnumT<T>::No &&
!CompoundT<T>::IsPtrT &&
!CompoundT<T>::IsRefT &&
!CompoundT<T>::IsArrayT &&
!CompoundT<T>::IsPtrMemT &&
!CompoundT<T>::IsFuncT };
enum { No = !Yes };
};
|
19.6 Putting It All Together
Now that we are able to classify any type according to its kind, it is convenient to group all the classifying templates in a single general-purpose template. The following relatively small header file does just that:
// types/typet.hpp
#ifndef TYPET_HPP
#define TYPET_HPP
// define IsFundaT<>
#include "type1.hpp"
// define primary template CompoundT<> (first version)
//#include "type2.hpp"
// define primary template CompoundT<> (second version)
#include "type6.hpp"
// define CompoundT<> specializations
#include "type3.hpp"
#include "type4.hpp"
#include "type5.hpp"
// define IsEnumT<>
#include "type7.hpp"
// define IsClassT<>
#include "type8.hpp"
// define template that handles all in one style
template <typename T>
class TypeT {
public:
enum { IsFundaT = IsFundaT<T>::Yes,
IsPtrT = CompoundT<T>::IsPtrT,
IsRefT = CompoundT<T>::IsRefT,
IsArrayT = CompoundT<T>::IsArrayT,
IsFuncT = CompoundT<T>::IsFuncT,
IsPtrMemT = CompoundT<T>::IsPtrMemT,
IsEnumT = IsEnumT<T>::Yes,
IsClassT = IsClassT<T>::Yes };
};
#endif // TYPET_HPP
The following program shows an application of all these classification templates:
// types/types.cpp
#include "typet.hpp"
#include <iostream>
class MyClass {
};
void myfunc()
{
}
enum E { e1 };
// check by passing type as template argument
template <typename T>
void check()
{
if (TypeT<T>::IsFundaT) {
std::cout << " IsFundaT ";
}
if (TypeT<T>::IsPtrT) {
std::cout << " IsPtrT ";
}
if (TypeT<T>::IsRefT) {
std::cout << " IsRefT ";
}
if (TypeT<T>::IsArrayT) {
std::cout << " IsArrayT ";
}
if (TypeT<T>::IsFuncT) {
std::cout << " IsFuncT ";
}
if (TypeT<T>::IsPtrMemT) {
std::cout << " IsPtrMemT ";
}
if (TypeT<T>::IsEnumT) {
std::cout << " IsEnumT ";
}
if (TypeT<T>::IsClassT) {
std::cout << " IsClassT ";
}
std::cout << std::endl;
}
// check by passing type as function call argument
template <typename T>
void checkT (T)
{
check<T>();
// for pointer types check type of what they refer to
if (TypeT<T>::IsPtrT || TypeT<T>::IsPtrMemT) {
check<typename CompoundT<T>::BaseT>();
}
}
int main()
{
std::cout << "int:" << std::endl;
check<int>();
std::cout << "int&:" << std::endl;
check<int&>();
std::cout << "char[42]:" << std::endl;
check<char[42]>();
std::cout << "MyClass:" << std::endl;
check<MyClass>();
std::cout << "ptr to enum:" << std::endl;
E* ptr = 0;
checkT(ptr);
std::cout << "42:" << std::endl;
checkT(42);
std::cout << "myfunc():" << std::endl;
checkT(myfunc);
std::cout << "memptr to array:" << std::endl;
char (MyClass::* memptr) [] = 0;
checkT(memptr);
}
The program has the following output:
int:
IsFundaT
int&:
IsRefT
char[42]:
IsArrayT
MyClass:
IsClassT
ptr to enum:
IsPtrT
IsEnumT
42:
IsFundaT
myfunc():
IsPtrT
IsFuncT
memptr to array:
IsPtrMemT
IsArrayT
|
19.7 Afternotes
The ability for a program to inspect its own high-level properties (such as its type structures) is sometimes called reflection. Our framework therefore implements a form of compile-time reflection, which turns out to be a powerful ally to metaprogramming (see Chapter 17).
The idea of storing properties of types as members of template specializations dates back to at least the mid-1990s. Among the earlier serious applications of type classification templates was the __type_traits utility in the STL implementation distributed by SGI (then known as Silicon Graphics). The SGI template was meant to represent some properties of its template argument (for example, whether it was a POD type or whether its destructor was trivial). This information was then used to optimize certain STL algorithms for the given type. An interesting feature of the SGI solution was that some SGI compilers recognized the __type_traits specializations and provided information about the arguments that could not be derived using standard techniques. (The generic implementation of the __type_traits template was safe to use, albeit suboptimal.)
The use of the SFINAE principle for type classification purposes had been noted when the SFINAE principle was clarified during the standardization effort. However, it was never formally documented, and as a result much effort was later spent trying to recreate some of the techniques described in this chapter. One of the notable early contributions was by Andrei Alexandrescu who made popular the use of the sizeof operator to determine the outcome of overload resolution.
Finally, we should note that a rather complete type classification template has been incorporated in the Boost library (see [BoostTypeTraits]). In turn, this implementation is the basis of an effort to add such a facility to the standard library. See also Section 13.10 on page 218 for a related language extension.

|
Chapter 20. Smart Pointers
Memory is a resource that is normally explicitly managed in C++ programs. This management involves the acquisition and disposal of blocks of raw memory.
One of the more delicate issues in managing dynamically allocated memory is the decision of when to deallocate it. Among the various tools to simplify this aspect of programming are so-called smart pointer templates. In C++, smart pointers are classes that behave somewhat like ordinary pointers (in that they provide the dereferencing operators -> and *) but in addition encapsulate some memory or resource management policy.
In this chapter we develop smart pointer templates that encapsulate two different ownership modelsexclusive and shared:
Exclusive ownership can be enforced with little overhead, compared with handling raw pointers. Smart pointers that enforce such a policy are useful to deal with exceptions thrown while manipulating dynamically allocated objects. Shared ownership can sometimes lead to excessively complicated object lifetime situations. In such cases, it may be advisable to move the burden of the lifetime decisions from the programmer to the program.
The term smart pointer implies that objects are being pointed to. Alternatives for function pointers are subject to different issues, some of which are discussed in Chapter 22.

|
20.1 Holders and Trules
This section introduces two smart pointer types: a holder type to hold an object exclusively and a so-called trule to enable the transfer of ownership from one holder to another.
20.1.1 Protecting Against Exceptions
Exceptions were introduced in C++ to improve the reliability of C++ programs. They allow regular and exceptional execution paths to be more cleanly separated. Yet shortly after exceptions were introduced, various C++ programming authors and columnists started observing that a naive use of exceptions leads to trouble, and particularly to memory leaks. The following example shows but one of the many troublesome situations that could arise:
void do_something()
{
Something* ptr = new Something;
// perform some computation with *ptr
ptr->perform();
…
delete ptr;
}
This function creates an object with new, performs some operations with this object, and destroys the object at the end of the function with delete. Unfortunately, if something goes wrong after the creation but before the deletion of the object and an exception gets thrown, the object is not deallocated and the program leaks memory. Other problems may arise because the destructor is not called (for example, buffers may not be written out to disk, network connections may not be released, on-screen windows may not be closed, and so forth). This particular case can be handled fairly easily using an explicit exception handler:
void do_something()
{
Something* ptr = 0;
try {
ptr = new Something;
// perform some computation with *ptr
ptr->perform();
…
}
catch (...) {
delete ptr;
throw; // rethrow the exception that was caught
}
return result;
}
This is manageable, but already we find that the exceptional path is starting to dominate the regular path, and the deletion of the object has to be done in two different places: once in the regular path and once in the exceptional path. This avenue quickly grows worse. Consider what happens if we need to create two objects in a single function:
void do_two_things()
{
Something* first = new Something;
first->perform();
Something* second = new Something;
second->perform();
delete second;
delete first;
}
Using an explicit exception handler, there are various ways to make this exception-safe, but none seems very appealing. Here is one option:
void do_two_things()
{
Something* first = 0;
Something* second = 0;
try {
first = new Something;
first->perform();
second = new Something;
second->perform();
}
catch (...) {
delete first;
delete second;
throw; // rethrow the exception that was caught
}
delete second;
delete first;
}
Here we made the assumption that the delete operations will not themselves trigger exceptions.
In this example, the exception handling code is a very large part of the routine, but more important, it could be argued that it is the most subtle part of it. The need for exception safety has also significantly changed the structure of the regular path of our routineperhaps more so than you may feel comfortable with.
20.1.2 Holders
Fortunately, it is not very hard to write a small class template that essentially encapsulates the policy in the second example. The idea is to write a class that behaves most like a pointer, but which destroys the object to which it points if it is itself destroyed or if another pointer is assigned to it. Such a class could be called a holder because it is meant to hold an object safely while we perform various computations. Here is how we could do this:
// pointers/holder.hpp
template <typename T>
class Holder {
private:
T* ptr; // refers to the object it holds (if any)
public:
// default constructor: let the holder refer to nothing
Holder() : ptr(0) {
}
// constructor for a pointer: let the holder refer to where the pointer refers
explicit Holder (T* p) : ptr(p) {
}
// destructor: releases the object to which it refers (if any)
~Holder() {
delete ptr;
}
// assignment of new pointer
Holder<T>& operator= (T* p) {
delete ptr;
ptr = p;
return *this;
}
// pointer operators
T& operator* () const {
return *ptr;
}
T* operator-> () const {
return ptr;
}
// get referenced object (if any)
T* get() const {
return ptr;
}
// release ownership of referenced object
void release() {
ptr = 0;
}
// exchange ownership with other holder
void exchange_with (Holder<T>& h) {
swap(ptr,h.ptr);
}
// exchange ownership with other pointer
void exchange_with (T*& p) {
swap(ptr,p);
}
private:
// no copying and copy assignment allowed
Holder (Holder<T> const&);
Holder<T>& operator= (Holder<T> const&);
};
Semantically, the holder takes ownership of the object to which ptr refers. This object has to be created with new, because delete is used whenever the object owned by the holder has to be destroyed.
The release() member removes control over the held object from the holder. However, the plain assignment operator is smart enough to destroy and deallocate any object held because another object will be held instead and the assignment operator does not return a holder or pointer for the original object. We added two exchange_with() members that allow us to replace conveniently the object being held without destroying it.
Our example with two allocations can be rewritten as follows:
void do_two_things()
{
Holder<Something> first(new Something);
first->perform();
Holder<Something> second(new Something);
second->perform();
}
This is much cleaner. Not only is the code exception-safe because of the work done by the Holder destructors, but the deletion is also automatically done when the function terminates through its regular path (at which point the objects indeed were to be destroyed).
Note that you can't use the assignment-like syntax for initialization:
Holder<Something> first = new Something; // ERROR
This is because the constructor is declared as explicit and there is a minor difference between
X x;
Y y(x); // explicit conversion
and
X x;
Y y = x; // implicit conversion
The former creates a new object of type Y by using an explicit conversion from type X, whereas the latter creates a new object of type Y by using an implicit conversion, but in our case implicit conversions are inhibited by the keyword explicit.
20.1.3 Holders as Members
We can also avoid resource leaks by using holders within a class. When a member has a holder type instead of an ordinary pointer type, we often no longer need to deal explicitly with that member in the destructor because the object to which it refers gets deleted with the deletion of the holder member. In addition, a holder helps to avoid resource leaks that are caused by exceptions that are thrown during the initialization of an object. Note that destructors are called only for those objects that are completely constructed. So, if an exception occurs inside a constructor, destructors are called only for member objects with a constructor that finished normally. Without holders, this may result in a resource leak if, for example, a first successful allocation was followed by an unsuccessful one. For example:
// pointers/refmem1.hpp
class RefMembers {
private:
MemType* ptr1; // referenced members
MemType* ptr2;
public:
// default constructor
// - will cause resource leak if second new throws
RefMembers ()
: ptr1(new MemType), ptr2(new MemType) {
}
// copy constructor
// - might cause resource leak if second new throws
RefMembers (RefMembers const& x)
: ptr1(new MemType(*x.ptr1)), ptr2(new MemType(*x.ptr2)) {
}
// assignment operator
const RefMembers& operator= (RefMembers const& x) {
*ptr1 = *x.ptr1;
*ptr2 = *x.ptr2;
return *this;
}
~RefMembers () {
delete ptr1;
delete ptr2;
}
…
};
By using holders instead of ordinary pointer members, we easily avoid these potential resource leaks:
// pointers/refmem2.hpp
#include "holder.hpp"
class RefMembers {
private:
Holder<MemType> ptr1; // referenced members
Holder<MemType> ptr2;
public:
// default constructor
// - no resource leak possible
RefMembers ()
: ptr1(new MemType), ptr2(new MemType) {
}
// copy constructor
// - no resource leak possible
RefMembers (RefMembers const& x)
: ptr1(new MemType(*x.ptr1)), ptr2(new MemType(*x.ptr2)) {
}
// assignment operator
const RefMembers& operator= (RefMembers const& x) {
*ptr1 = *x.ptr1;
*ptr2 = *x.ptr2;
return *this;
}
// no destructor necessary
// (default destructor lets ptr1 and ptr2 delete their objects)
…
};
Note that although we can now omit a user-defined destructor, we still have to program the copy constructor and the assignment operator.
20.1.4 Resource Acquisition Is Initialization
The general idea supported by holders is a pattern called resource acquisition is initialization or just RAII, which was introduced in [StroustrupDnE]. By introducing template parameters for deallocation policies, we can replace all code that matches the following outline:
void do()
{
// acquire resources
RES1* res1 = acquire_resource_1();
RES2* res2 = acquire_resource_2();
…
// release resources
release_resource_2(res);
release_resource_1(res);
}
with
void do()
{
// acquire resources
Holder<RES1,… > res1(acquire_resource_1());
Holder<RES2,… > res2(acquire_resource_2());
…
}
This can be done by something similar to our uses of Holder, with the added advantage that the code is exception-safe.
20.1.5 Holder Limitations
Not every problem is resolved with our implementation of the Holder template. Consider the following example:
Something* load_something()
{
Something* result = new Something;
read_something(result);
return result;
}
In this example, two things make the code more complicated:
Inside the function, read_something(), which is a function that expects an ordinary pointer as its argument, is called. load_something() returns an ordinary pointer.
Now, using a holder, the code becomes exception-safe but more complicated:
Something* load_something()
{
Holder<Something> result(new Something);
read_something(result.get_pointer());
Something* ret = result.get_pointer();
result.release();
return ret;
}
Presumably, the function read_something() is not aware of the Holder type; hence we must extract the real pointer using the member function get_pointer(). By using this member function, the holder keeps control over the object, and the recipient of the result of the function call should understand that it does not own the object whose pointer it getsthe holder does.
If no get_pointer() member function is provided, we can also use the user-defined indirection operator *, followed by the built-in address-of operator &. Yet another alternative is to call operator -> explicitly. The following example illustrates this:
read_something(&*result);
read_something(result.operator->());
You'll probably agree that the latter is a particularly ugly alternative. However, it may be appropriate to attract the attention to the fact that something relatively dangerous is being done.
Another issue in the example code is that we must call release() to cancel the ownership of the object being referred to. This prevents that object from being destroyed when the function is done; hence it can be returned to the caller. Note that we must store the return value in a temporary variable before releasing it:
Something* ret = result.get_pointer();
result.release();
return ret;
To avoid this, we can enable statements such as
return result,release();
by modifying release() so that it returns the object previously owned:
template <typename T>
class Holder {
…
T* release() {
T* ret = ptr;
ptr = 0;
return ret;
}
…
};
This leads to an important observation: Smart pointers are not that smart, but used with a simple consistent policy they do make life much simpler.
20.1.6 Copying Holders
You probably noticed that in our implementation of the Holder template we disabled copying of holders by making the copy constructor and the copy-assignment operator private. Indeed, the purpose of copying is usually to obtain a second object that is essentially identical to the original. For a holder this would mean that the copy also thinks it controls when the object gets deallocated, and chaos ensues because both holders are inclined to deallocate the controlled object. Thus, copying is not an appropriate operation for holders. Instead, we can conceive of transfer as being the natural counterpart of copying in this case.
A transfer operation is fairly easily achieved using a release operation followed by initialization or assignment, as shown in the following:
Holder<Something> h1(new Something);
Holder<Something> h2(h1.release());
Note again that the syntax
Holder<X> h = p;
will not work because it implies an implicit conversion whereas the constructor is declared as explicit:
Holder<Something> h2 = h1.release(); // ERROR
20.1.7 Copying Holders Across Function Calls
The explicit transfer works well, but the situation is a little more subtle when the transfer is across a function call. For the case of passing a holder from a caller to a callee, we can always pass by reference instead of passing by value. Using the "release followed by initialization" approach can lead to problems when more than one argument is passed:
MyClass x;
callee(h1.release(),x); // passing x may throw!
If the compiler chooses first to cause h1.release() to be evaluated, then the subsequent copying of x (assuming it is passed by value) may trigger an exception that occurs, whereas no component is in charge of releasing the object that used to be owned by holder h1. Hence, a holder should always be passed by reference.
Unfortunately, it is in general not convenient to return a holder by reference because this requires the holder to have a lifetime that exceeds the function call, which in turn makes it unclear when and how the holder will deallocate the object under its control. You can build an argument that it is fine to call release() on a holder just prior to returning the encapsulated pointer. This is essentially what we did with load_something() earlier. Consider the following situation:
Something* creator()
{
Holder<Something> h(new Something);
MyClass x; // for illustration purposes
return h.release();
}
We must be aware here that the destruction of x could cause an exception to be thrown after h has released the object it owned and before that object was placed under the control of another entity. If so, we would again have a resource leak. (Allowing exceptions to escape from destructors is rarely a good idea: It makes it easy for an exception to be thrown while the call stack is being unwound for a previous exception, and this leads to immediate termination of the program. The latter situation can be guarded against, but it makes for harder to understandand therefore more brittlecode.)
20.1.8 Trules
To solve such problems let's introduce a helper class template dedicated to transferring holders. We call this class template a trule, which is a term derived from the contraction of transfer capsule. Here is its definition:
// pointers/trule.hpp
#ifndef TRULE_HPP
#define TRULE_HPP
template <typename T>
class Holder;
template <typename T>
class Trule {
private:
T* ptr; // objects to which the trule refers (if any)
public:
// constructor to ensure that a trule is used only as a return type
// to transfer holders from callee to caller!
Trule (Holder<T>& h) {
ptr = h.get();
h.release();
}
// copy constructor
Trule (Trule<T> const& t) {
ptr = t.ptr;
const_cast<Trule<T>&>(t).ptr = 0;
}
// destructor
~Trule() {
delete ptr;
}
private:
Trule(Trule<T>&); // discourage use of lvalue trules
Trule<T>& operator= (Trule<T>&); // discourage copy assignment
friend class Holder<T>;
};
#endif // TRULE_HPP
Clearly, something ugly is going on in the copy constructor. Because transfer capsules are meant as the return type of functions that wish to transfer holders, they always occur as temporary objects (rvalues); hence they can be bound only to reference-to-const types. However, the transfer cannot just be a copy and must remove the ownership, by nulling the encapsulated pointer, from the original Trule. The latter operation is intrinsically non-const. This state of affairs is ugly, but it is in fact legal to cast away constness in these cases because the original object was not declared const. Hence, we must be careful to declare the return type of a function transferring a holder as Trule<T> and not Trule<T> const.
Note that no such code is used for converting a holder into a trule: The holder must be a modifiable lvalue. This is why we use a separate type for the transfer capsule instead of merging this functionality into the Holder class template.
To discourage the use of Trule as anything but a return type for transferring holders, a copy constructor taking a reference to a non-const object and a similar copy-assignment operator were declared private. This prevents us from doing much with lvalue Trules, but it is only a very partial measure. The goal of a trule is to help the responsible software engineer, not to thwart the mad scientist.
The Trule template is not complete until it is recognized by the Holder template:
// pointers/holder2extr.hpp
template <typename T>
class Holder {
// previously defined members
…
public:
Holder (Trule<T> const& t) {
ptr = t.ptr;
const_cast<Trule<T>&>(t).ptr = 0;
}
Holder<T>& operator= (Trule<T> const& t) {
delete ptr;
ptr = t.ptr;
const_cast<Trule<T>&>(t).ptr = 0;
return *this;
}
};
To illustrate this refined Holder/Trule pair, we can rewrite our load_something() example and invent a caller for it:
// pointers/truletest.cpp
#include "holder2.hpp"
#include "trule.hpp"
class Something {
};
void read_something (Something* x)
{
}
Trule<Something> load_something()
{
Holder<Something> result(new Something);
read_something(result.get());
return result;
}
int main()
{
Holder<Something> ptr(load_something());
…
}
To conclude, we have created a pair of class templates that are almost as convenient to use as plain pointers with the added benefit of managing the deallocation of objects necessary when the stack gets unwound as the result of an exception being thrown.

|
20.2 Reference Counting
The Holder template (and its Trule helper) works well to hold allocated structures temporarily so that they will be deallocated if an exception causes the local stack frame to be unwound. However, memory leaks can also occur in other contexts, and in particular when many objects are interconnected in complex structures.
A general rule about the management of dynamically allocated objects is easily stated: If nothing in an application points to a dynamically allocated object, that object should be destroyed and its storage should be made available for reuse. It is therefore not surprising that programmers everywhere have been looking for ways to automate such a policy. The challenge is to determine that nothing is pointing to an object.
One idea that has been implemented many times over is so-called reference counting: For each object that is pointed to, keep a count of the number of pointers to it, and when that count drops to zero, delete the object. For this to be feasible in C++, we need to adhere to some convention. Specifically, because it is not practical to track how ordinary pointers to an object are created, copied, and destroyed, it is common to require that the only "pointers" to a reference-counted object are a specific kind of smart pointer. In this section we discuss the implementation of such a reference-counting smart pointer. This pointer is a template whose main parameter is the type of the object to which it points:
template <typename T … >
class CountingPtr {
public:
// a constructor that starts a new count for the object
// pointed to by T:
explicit CountingPtr (T*);
// copying increases the count:
CountingPtr (CountingPtr<T… > const&);
// destruction decreases the count:
inline ~CountingPtr();
// assignment decreases the count for the object previously
// pointed to and increases it for the new object pointed to
// (but beware of self-assignment):
CountingPtr<T… >& operator= (CountingPtr<T… > const&);
// the operators that make this a smart pointer:
inline T& operator* ();
inline T* operator-> ();
…
};
The parameter T is the only parameter that is truly needed to build a functional counting pointer template. Indeed, a good case can be made in favor of keeping a basic template like this as simple and reliable as possible. Nonetheless, we choose to use CountingPtr to demonstrate policy parameters (a concept described in detail in Chapter 15).
The comments in the code explain the general approach to reference counting: Every construction, destruction, and assignment of a CountingPtr may potentially change the reference counts (when one of the counts drops to zero, the object pointed to is deleted).
20.2.1 Where Is the Counter?
Because our idea is to count the number of pointers to an object, it would be entirely logical to place the counter in the object. Unfortunately, this is not viable when the type of the object pointed to has been designed without reference counting in mind.
If no counter is available in a reference-counted object, the counter must be allocated in a separate storage area that is at least as long-lived as the object pointed to; in other words, it must be dynamically allocated. Using the plain ::operator new that comes with your C++ compiler is likely to re-sult in disappointing performance. Indeed, ::operator new must be able to allocate quasi-arbitrary object sizes without excessive storage overhead, and this requires some computational compromises. Instead, for counting pointers it is more common to use a special-purpose allocator.
A less common alternative to the separate allocation of a counter is to use a special-purpose allocator for the reference-counted object. Indeed, such an allocator could allocate some extra storage to keep the counter.
Instead of prescribing where the counter is located, we leave the location of the counter as a template parameter. In effect, this parameter is our counter policy (see Chapter 15). This policy's interface could consist simply of a function returning an integer type and one that allocates that integer if necessary. However, there are good reasons to provide a slightly higher level interface.
20.2.2 Concurrent Counter Access
In an environment with only one thread of execution, managing the counter is straightforward. Incrementing, decrementing, and testing for equality with zero are basic operations. However, in multi-threaded environments a counter can be shared by smart pointers operating in different threads of execution. In this case we may need to add smart pointers to the counter itself so that, for example, simultaneous increment operations from two threads are appropriately sequenced. In practice this requires a form of (implicit or explicit) locking.
Rather than specifying how this locking is done, we specify for the counter an interface that is of a sufficiently high level to introduce locking operations. Specifically, we require that a counter be a class with the following interface:
class CounterPolicy {
public:
// the following four special members (constructors, destructor, and
// copy assignment) need not be declared explicitly in some cases,
// but they must be accessible
CounterPolicy();
CounterPolicy(CounterPolicy const&);
~CounterPolicy();
CounterPolicy& operator=(CounterPolicy const&);
// assume T is the type of object pointed to
void init(T*); // initialization to one, possibly allocation
void dispose(T*); // possibly involves deallocation of the counter
void increment(T*); // atomic increment by one
void decrement(T*); // atomic decrement by one
bool is_zero(T*); // check for zero
…
};
The type T used in this interface is presumably provided as a template parameter. It is used only by policies that use the object pointed to to store the counter.
Locking the counter protects concurrent access only to the counter and not to the CountingPtr itself. Hence, if multiple smart pointers to a unique object are shared among different threads of execution, an application may need to introduce additional locks to sequence the CountingPtr operations correctly. The smart pointer itself, however, cannot be held responsible for locking at that level.
20.2.3 Destruction and Deallocation
When no counting pointers are pointing to an object, our policy is to dispose of that object. In C++ this can often be achieved using the standard delete operator. However, this is not always the case. Sometimes objects must be deallocated using different functions, such as the standard C function free(). Furthermore, if the object pointed to is really an array, the disposal may need to use operator delete[].
Because we anticipate that there are sufficient cases when the disposal of the object will be nonstandard, it is worthwhile to introduce a separate object policy for it. Its interface is very simple:
class ObjectPolicy {
public:
// the following four special members (constructors, destructor, and
// copy assignment) need not be declared explicitly in some cases,
// but they must be accessible
ObjectPolicy();
ObjectPolicy(CounterPolicy const&);
~ObjectPolicy();
ObjectPolicy& operator=(ObjectPolicy const&);
// assume T is the type of object pointed to
void dispose (T*);
};
It is possible to enrich this policy for other operations that may involve the object pointed to (for example, the operator* and operator-> dereferencing operators). One popular option is to incorporate some checking against dereferencing our smart pointer when it is not actually pointing to any object. On the other hand it is also entirely possible to add a specific policy parameter for this sort of checking. In the interest of brevity we do not pursue this option, but it is not hard to implement if you are comfortable with the remainder of this section.
For most objects counted by CountingPtrs, we can use the following simple object policy:
// pointers/stdobjpolicy.hpp
class StandardObjectPolicy {
public:
template<typename T> void dispose (T* object) {
delete object;
}
};
Clearly, this does not work for arrays allocated with operator new[]. A replacement policy for this case is trivial, fortunately:
// pointers/stdarraypolicy.hpp
class StandardArrayPolicy {
public:
template<typename T> void dispose (T* array) {
delete[] array;
}
};
Note that in both cases we chose to implement dispose() as a member template. We could also have parameterized the policy class instead. A discussion of such alternatives can be found in Section 15.1.6 on page 259.
20.2.4 The CountingPtr Template
Now that we have decided our policy interfaces, we are ready to implement the CountingPtr interface itself:
// pointers/countingptr.hpp
template<typename T,
typename CounterPolicy = SimpleReferenceCount,
typename ObjectPolicy = StandardObjectPolicy>
class CountingPtr : private CounterPolicy, private ObjectPolicy {
private:
// shortcuts:
typedef CounterPolicy CP;
typedef ObjectPolicy OP;
T* object_pointed_to; // the object referred to (or NULL if none)
public:
// default constructor (no explicit initialization):
CountingPtr() {
this->object_pointed_to = NULL;
}
// a converting constructor (from a built-in pointer):
explicit CountingPtr (T* p) {
this->init(p); // init with ordinary pointer
}
// copy constructor:
CountingPtr (CountingPtr<T,CP,OP> const& cp)
: CP((CP const&)cp), // copy policies
OP((OP const&)cp) {
this->attach(cp); // copy pointer and increment counter
}
// destructor:
~CountingPtr() {
this->detach(); // decrement counter
// (and dispose counter if last owner)
}
// assignment of a built-in pointer
CountingPtr<T,CP,OP>& operator= (T* p) {
// no counting pointer should point to *p yet:
assert(p != this->object_pointed_to);
this->detach(); // decrement counter
// (and dispose counter if last owner)
this->init(p); // init with ordinary pointer
return *this;
}
// copy assignment (beware of self-assignment):
CountingPtr<T,CP,OP>&
operator= (CountingPtr<T,CP,OP> const& cp) {
if (this->object_pointed_to != cp.object_pointed_to) {
this->detach(); // decrement counter
// (and dispose counter if last owner)
CP::operator=((CP const&)cp); // assign policies
OP::operator=((OP const&)cp);
this->attach(cp); // copy pointer and increment counter
}
return *this;
}
// the operators that make this a smart pointer:
T* operator-> () const {
return this->object_pointed_to;
}
T& operator* () const {
return *this->object_pointed_to;
}
// additional interfaces will be added later
…
private:
// helpers:
// - init with ordinary pointer (if any)
void init (T* p) {
if (p != NULL) {
CounterPolicy::init(p);
}
this->object_pointed_to = p;
}
// - copy pointer and increment counter (if any)
void attach (CountingPtr<T,CP,OP> const& cp) {
this->object_pointed_to = cp.object_pointed_to;
if (cp.object_pointed_to != NULL) {
CounterPolicy::increment(cp.object_pointed_to);
}
}
// - decrement counter (and dispose counter if last owner)
void detach() {
if (this->object_pointed_to != NULL) {
CounterPolicy::decrement(this->object_pointed_to);
if (CounterPolicy::is_zero(this->object_pointed_to)) {
// dispose counter, if necessary:
CounterPolicy::dispose(this->object_pointed_to);
// use object policy to dispose the object pointed to:
ObjectPolicy::dispose(this->object_pointed_to);
}
}
}
};
There is relatively little complexity in this template, except perhaps for that fact that the copy-assignment operation must be careful with the self-assignment case. Indeed, in most cases the assignment operator can just detach the counting pointer from the object to which it used to point, thereby possibly decreasing the associated counter to zero and disposing of the object. However, if this happens when the counting pointer is assigned to itself, this disposal is premature (and incorrect).
Note also that we must explicitly check for the null pointer case because a null pointer does not have an associated counter. An alternative to our approach is to leave the checking to the policy classes. In fact, a possible policy could be not to allow null CountingPtrs at all. When such a policy is applicable, it results in slightly improved performance.
We use inheritance to include the policies. This ensures that if the policies are empty classes, they do not need to take up storage (provided our compiler implements the empty base class optimization, see Section 16.2 on page 289). We could use the BaseMemberPair template introduced in Section 16.2.2 on page 294 to avoid having the members of the policy classes be visible in the smart pointer class. In this example we chose to avoid making the source code more complicated for the sake of keeping the discussion simpler.
Because there is more than one default template argument, it could be beneficial to use the technique of Section 16.1 on page 285 to override the defaults conveniently and selectively. Again, we did not do so here for the sake of brevity.
20.2.5 A Simple Noninvasive Counter
Although we have completed the design of our CountingPtr, we haven't actually finished implementing the design. There is no code yet for a counter policy. Let's first look at a policy for a counter that is not stored in the object pointed tothat is, a noninvasive (or nonintrusive) counter policy.
The main issue with our counter is its allocation. Indeed, the counter may need to be shared by many CountingPtrs; hence it must be given a lifetime that lasts until the last smart pointer is destroyed. Usually this is done using a special-purpose allocator specialized for the allocation of small objects of a fixed size. However, because the design of such allocators is not particularly pertinent to the topic of C++ templates, we forgo the in-depth discussion of an industrial-strength allocator.
Instead, let's assume the existence of functions alloc_counter() and dealloc_counter() that manage storage of type size_t. With these assumptions, we can write our simple counter as follows:
// pointers/simplerefcount.hpp
#include <stddef.h> // for the definition of size_t
#include "allocator.hpp"
class SimpleReferenceCount {
private:
size_t* counter; // the allocated counter
public:
SimpleReferenceCount () {
counter = NULL;
}
// default copy constructor and copy-assignment operator
// are fine in that they just copy the shared counter
public:
// allocate the counter and initialize its value to one:
template<typename T> void init (T*) {
counter = alloc_counter();
*counter = 1;
}
// dispose of the counter:
template<typename T> void dispose (T*) {
dealloc_counter(counter);
}
// increment by one:
template<typename T> void increment (T*) {
++*counter;
}
// decrement by one:
template<typename T> void decrement (T*) {
--*counter;
}
// test for zero:
template<typename T> bool is_zero (T*) {
return *counter == 0;
}
};
Because this policy is nonempty (it stores a pointer to the counter), it increases the size of a CountingPtr. The size can be reduced by storing the pointer to the object alongside the counter instead of placing it directly in the smart pointer class. Doing so requires a change in our policy design and decreases the performance of accessing the object by requiring an additional level of indirection.
Note also that this particular policy doesn't make use of the counted object itself. In other words, the parameter passed to its member functions is never used. In the following section we see an alternative policy that does make use of this parameter.
20.2.6 A Simple Invasive Counter Template
An invasive (or intrusive) counter policy is one that places the counter in the type of the managed objects themselves (or perhaps in some storage controlled by these managed objects). This normally needs to be designed at the time the object type is designed; hence the solution is likely to be very specific to that type. However, for illustrative purposes we develop a more generic invasive policy.
To select the location of the counter in the referenced object let's use a nontype pointer-to-member parameter. Because the counter is allocated as part of the object, the implementation of this policy is in some ways simpler than our noninvasive example, but the pointer-to-member syntax is a little less common:
// pointers/memberrefcount.hpp
template<typename ObjectT, // the class type containing the counter
typename CountT, // the type of the pointer
CountT ObjectT::*CountP> // the location of the counter
class MemberReferenceCount
{
public:
// the default constructor and destructor are fine
// initialize the counter to one:
void init (ObjectT* object) {
object->*CountP = 1;
}
// no action is needed to dispose of the counter:
void dispose (ObjectT*) {
}
// increment by one:
void increment (ObjectT* object) {
++object->*CountP;
}
// decrement by one:
void decrement (ObjectT* object) {
--object->*CountP;
}
// test for zero:
template<typename T> bool is_zero (ObjectT* object) {
return object->*CountP == 0;
}
};
This policy allows a class implementer to provide a reference-counting pointer type quickly for the class. The outline of the design of such a class could be as follows:
class ManagedType {
private:
size_t ref_count;
public:
typedef CountingPtr<ManagedType,
MemberReferenceCount
<ManagedType,
size_t,
&ManagedType::ref_count> >
Ptr;
…
};
With this approach, ManagedType::Ptr is a convenient way to refer to the smart pointer type that should be used to access a ManagedType object.
20.2.7 Constness
In C++ the types X const* and X* const are distinct. The former indicates that the element pointed to should not be modified, whereas the latter indicates that the pointer itself cannot be modified. The same duality exists with our reference counting pointer: X const* corresponds to CountingPtr<X const> whereas X* const corresponds to CountingPtr<X> const. In other words, the constness of the object pointed to is a property of the template argument. Let's look at some of the public member functions of CountingPtr to see how they are affected by this observation.
The dereferencing operators do not modify the pointer, which is why they are const member functions. However, they do provide access to the object pointed to. Because the constness of this object is captured by the template parameter T, T can be used without added qualification in the return type of these operators.
An int* cannot be initialized by an int const* because this would create a way to modify an object through an entity that wasn't meant to provide that kind of mutable access. In the same vein, we must ensure that a CountingPtr<int> cannot be initialized by a CountingPtr<int const> or even by a int const*. Again, using the plain (not const-qualified) template parameter T achieves the desired effect. This may seem straightforward, but smart pointer implementations that declare a constructor or assignment operator accepting a T const* are quite common (and presumably erroneous).
The assignment operators are subject to the same observations as the constructors. Naturally, such operators are never const themselves.
20.2.8 Implicit Conversions
Built-in pointers are subject to several implicit conversions:
Conversion to void* Conversion to a pointer to a base subobject of the object pointed to Conversion to bool (false if the pointer is null, true otherwise)
We may want to emulate these in our CountingPtr template, but doing so is not trivial, as we shall see. In addition, some programmers like their smart pointers to have a conversion to a corresponding built-in pointer type (for example, some like CountingPtr<int const> to be convertible to int const*).
Unfortunately, enabling implicit conversions to built-in pointer types creates a loophole in the assumption that all the pointers to a reference-counted object are CountingPtrs. We therefore choose not to provide such a conversion. Therefore, a CountingPtr<X> cannot implicitly be converted to void* or to X*.
Other drawbacks to implicit conversions to built-in pointer types include (assume cp is an counting pointer):
delete cp; and ::delete cp; become valid All sorts of meaningless pointer arithmetic goes undiagnosed (for example, cp[n], cp2 - cp1, and so forth)
On the other hand, implicit conversions to other CountingPtr specializations can make perfect sense. For example, we can imagine an implicit conversion to CountingPtr<void> (the latter can be a useful opaque pointer type, just like void*). There is a limitation, however: An invasive counter policy cannot accommodate such a conversion because the void type doesn't contain a counter. Similarly, a base class may not be compatible with an invasive counter policy either.
Nonetheless, we can add such implicit conversions to our CountingPtr template. Instantiation errors occur when attempting conversions that are not compatible with a given counter policy. The implicit conversions might look as follows:
template<typename T,
typename CounterPolicy = SimpleReferenceCount,
typename ObjectPolicy = StandardObjectPolicy>
class CountingPtr : private CounterPolicy, private ObjectPolicy {
private:
// Shortcuts:
typedef CounterPolicy CP;
typedef ObjectPolicy OP;
…
public:
// add a converting constructor and make sure it can access
// the private components of other instantiations:
friend template<typename T2, typename CP2, typename OP2>
class CountingPtr;
template <typename S> // S could be void or a base of T
CountingPtr(CountingPtr<S, OP, CP> const& cp)
: OP((OP const&)cp),
CP((CP const&)cp),
object_pointed_to(cp.object_pointed_to) {
if (cp.object_pointed_to != NULL) {
CP::increment(cp.object_pointed_to);
}
}
};
Note that in this case a converting constructor more easily enabled the desired implicit conversions than a conversion operator. In particular, we must make sure that the reference count is correctly copied.
The conversion to bool may seem straightforward. We can just add a user-defined conversion operator to CountingPtr:
template<typename T,
typename CounterPolicy = SimpleReferenceCount,
typename ObjectPolicy = StandardObjectPolicy>
class CountingPtr : private CounterPolicy, private ObjectPolicy {
…
public:
operator bool() const {
return this->object_pointed_to != (T*)0;
}
};
This works, but it also allows surprising and unintentional operations on CountingPtrs. For example, with this conversion in place, we can add two CountingPtrs! This is sufficiently serious that we prefer not to provide that operator.
The conversion to bool is mostly useful to support constructs of the form
if (cp) …
or
while (!cp) …
Therefore, this problem has traditionally been worked around by providing a conversion to void* (which in turn is implicitly converted to bool in just the right places).
This approach has its own drawbacks in general, but it has them especially for a smart pointer for which we already decided not to provide an implicit conversion to void*.
A simple (but often overlooked) solution to this problem is to define a conversion to a pointer-to-member type instead of to a built-in type. Indeed, pointer-to-member types also support implicit conversion to bool, but unlike regular pointers they're not valid types for operator delete or for pointer arithmetic. The following addition to our CountingPtr template illustrates how to apply this technique:
template<typename T,
typename CounterPolicy = SimpleReferenceCount,
typename ObjectPolicy = StandardObjectPolicy>
class CountingPtr : private CounterPolicy, private ObjectPolicy {
…
private:
class BoolConversionSupport {
int dummy;
};
public:
operator BoolConversionSupport::*() const {
return this->object_pointed_to
? &BoolConversionSupport::dummy
: 0;
}
…
};
Note that this does not increase the size of a CountingPtr because no data members are added. By using a private nested class we avoid potential conflicts with client code.
20.2.9 Comparisons
We conclude our discussion of counting pointers with the development of various comparison operators for such pointers. Built-in pointers support both equality operators (== and !=) and ordering operators (<, <=, and so forth).
For built-in pointers, ordering operators are guaranteed to work only on two pointers that point to the same array, but this is not a useful scenario for counting pointers. Counting pointers always point to a single object or to the head of an array. Thus, we don't discuss these operators in the text that follows. (However, the operators could be implemented for CountingPtr along the same lines as the equality operators if an ordering was needed among CountingPtrs.)
Here are the details of operator == (operator != is similar):
template<typename T,
typename CounterPolicy = SimpleReferenceCount,
typename ObjectPolicy = StandardObjectPolicy>
class CountingPtr : private CounterPolicy, private ObjectPolicy {
…
public:
friend bool operator==(CountingPtr<T,CP,OP> const& cp,
T const* p) {
return cp == p;
}
friend bool operator==(T const* p,
CountingPtr<T,CP,OP> const& cp) {
return p == cp;
}
};
template <typename T1, typename T2,
typename CP, typename OP>
inline
bool operator== (CountingPtr<T1,CP,OP> const& cp1,
CountingPtr<T2,CP,OP> const& cp2)
{
return cp1.operator->() == cp2.operator->();
}
The out-of-class operator is a template, which allows us to compare counting pointers to different types. Its implementation allows us to demonstrate that it is possible to extract the built-in pointer encapsulated by CountingPtr. The explicit operator-> invocation that this requires is unusual enough to draw our attention that something potentially unsafe is going on.
Two other operators are provided as nontemplate operators. Because these operators still must depend on template parameters, they must be implemented as in-class friend definitions. Because they are nontemplates, the ordinary implicit conversions apply to their arguments. This includes the implicit conversion of zero to a null pointer value.

|
20.3 Afternotes
Smart pointer templates are probably the second-most obvious application of templates after container templates; however, the details are far from obvious, as this chapter illustrates. Indeed, many authors cover the topic in some detail. Good material supplementing our discussion can be found in [MeyersMoreEffective], which offers a more basic discussion, and in [AlexandrescuDesign], which describes a complete, policy-based design of a family of smart pointers.
The C++ standard library contains a smart pointer template auto_ptr. It is intended for the same use as our Holder/Trule pair of templates, but avoids the use of a second template by exploiting a controversial piece of the C++ overloading rules in the context of variable initialization.
Other smart pointers were proposed for inclusion in the C++ standard library, but the C++ standardization committee decided not to support them.
The Boost project offers a library containing a variety of smart pointer classes to meet a variety of needs (see [BoostSmartPtr]).

|
Chapter 21. Tuples
Throughout this book we often use homogeneous containers and array-like types to illustrate the power of templates. Such homogeneous structures extend the concept of a C/C++ array and are pervasive in most applications. C++ (and C) also has a nonhomogeneous containment facility: the class (or struct). Tuples are class templates that similarly allow us to aggregate objects of differing types. We start with the duoan entity analogous to the standard std::pair templatebut we also show how it can be nested to assemble an arbitrary number of members, thereby forming trios, quartets, and so forth.

|
21.1 Duos
A duo is the assembly of two objects into a single type. This is similar to the std::pair class template in the standard library, but because we will add slightly different functionality to this very basic utility, we opted for a name other than pair to avoid confusion with the standard item. At its very simplest, we can define Duo as follows:
template <typename T1, typename T2>
struct Duo {
T1 v1; // value of first field
T2 v2; // value of second field
};
This can, for example, be useful as a return type for a function that may return an invalid result:
Duo<bool,X> result = foo();
if (result.v1) {
// result is valid; value is in result.v2
…
}
Many other applications are possible.
The benefit of Duo as defined here is not insignificant, but it is rather small. After all, it would not be that much work to define a structure with two fields, and doing so allows us to choose meaningful names for these fields. However, we can extend the basic facility in a few ways to add to the convenience. First, we can add constructors:
template <typename T1, typename T2>
class Duo {
public:
T1 v1; // value of first field
T2 v2; // value of second field
// constructors
Duo() : v1(), v2() {
}
Duo (T1 const& a, T2 const& b)
: v1(a), v2(b) {
}
};
Note that we used an initializer list for the default constructor so that the members get zero initialized for built-in types (see Section 5.5 on page 56).
To avoid the need for explicit type parameters, we can further add a function so that the field types can be deduced:
template <typename T1, typename T2>
inline
Duo<T1,T2> make_duo (T1 const& a, T2 const& b)
{
return Duo<T1,T2>(a,b);
}
Now the creation and initialization of a Duo becomes more convenient. Instead of
Duo<bool,int> result;
result.v1 = true;
result.v2 = 42;
return result;
we can write
return make_duo(true,42);
Good C++ compilers can optimize this well enough so that this generates code equivalent to
return Duo<bool,int>(true,42);
Another refinement is to provide access to the field types, so that adapter templates can be built on top of Duo:
template <typename T1, typename T2>
class Duo {
public:
typedef T1 Type1; // type of first field
typedef T2 Type2; // type of second field
enum { N = 2 }; // number of fields
T1 v1; // value of first field
T2 v2; // value of second field
// constructors
Duo() : v1(), v2() {
}
Duo (T1 const& a, T2 const& b)
: v1(a), v2(b) {
}
};
At this stage we're rather close to the implementation of std::pair with the following differences:
We use different names. We provide a member N for the number of fields. We have no member template initialization to allow implicit type conversions during construction. We don't provide comparison operators.
A more powerful and cleaner implementation might looks as follows:
// tuples/duo1.hpp
#ifndef DUO_HPP
#define DUO_HPP
template <typename T1, typename T2>
class Duo {
public:
typedef T1 Type1; // type of first field
typedef T2 Type2; // type of second field
enum { N = 2 }; // number of fields
private:
T1 value1; // value of first field
T2 value2; // value of second field
public:
// constructors
Duo() : value1(), value2() {
}
Duo (T1 const & a, T2 const & b)
: value1(a), value2(b) {
}
// for implicit type conversion during construction
template <typename U1, typename U2>
Duo (Duo<U1,U2> const & d)
: value1(d.v1()), value2(d.v2()) {
}
// for implicit type conversion during assignments
template <typename U1, typename U2>
Duo<T1, T2>& operator = (Duo<U1,U2> const & d) {
value1 = d.value1;
value2 = d.value2;
return *this;
}
// field access
T1& v1() {
return value1;
}
T1 const& v1() const {
return value1;
}
T2& v2() {
return value2;
}
T2 const& v2() const {
return value2;
}
};
// comparison operators (allow mixed types):
template <typename T1, typename T2,
typename U1, typename U2>
inline
bool operator == (Duo<T1,T2> const& d1, Duo<U1,U2> const& d2)
{
return d1.v1()==d2.v1() && d1.v2()==d2.v2();
}
template <typename T1, typename T2,
typename U1, typename U2>
inline
bool operator != (Duo<T1,T2> const& d1, Duo<U1,U2> const& d2)
{
return !(d1==d2);
}
// convenience function for creation and initialization
template <typename T1, typename T2>
inline
Duo<T1,T2> make_duo (T1 const & a, T2 const & b)
{
return Duo<T1,T2>(a,b);
}
#endif // DUO_HPP
We made the following changes:
We made the data members private and added access functions. With the explicit initialization of both members in the default constructor
template <typename T1, typename T2>
class Duo {
…
Duo() : value1(), value2() {
}
…
} we made sure that values of built-in types are zero initialized (see Section 5.5 on page 56).
We provided member templates so that construction and initialization are possible with mixed types. We provided comparison operators == and !=. Note that we introduced separate sets of template parameters for both sides of a comparison to allow for comparisons of mixed types.
All the member templates are used to enable mixed type operations. That is, we can initialize, assign, and compare a Duo for which an implicit type conversion is necessary to perform the task. For example:
// tuples/duo1.cpp
#include "duo1.hpp"
Duo<float,int> foo ()
{
return make_duo(42,42);
}
int main()
{
if (foo() == make_duo(42,42.0)) {
…
}
}
In this program, in foo() there is a conversion from the return type of make_duo(), Duo<int,int> to the return type of foo(), Duo<float,int>. Similarly, the return value of foo() is compared with the return value of make_duo(42, 42.0), which is a Duo<int,double>.
It would not be difficult to add Trio and other templates to collect larger numbers of values. However, a more structured alternative can be obtained by nesting Duo objects. This idea is developed in the following sections.
|
21.2 Recursive Duos
Consider the following object definition:
Duo<int, Duo<char, Duo<bool, double> > > q4;
The type of q4 is a so-called recursive duo. It is a type instantiated from the Duo template, and the second type argument is itself a Duo as well. We could also use recursion of the first parameter, but in the remainder of this discussion, recursive duo refers only to Duos with a second template argument that is instantiated from the Duo template.
21.2.1 Number of Fields
It's relatively straightforward to count that q4 collects four values of types int, char, bool, and double respectively. To facilitate the formal counting of the number of fields, we can further partially specialize the Duo template:
// tuples/duo2.hpp
template <typename A, typename B, typename C>
class Duo<A, Duo<B,C> > {
public:
typedef A T1; // type of first field
typedef Duo<B,C> T2; // type of second field
enum { N = Duo<B,C>::N + 1 }; // number of fields
private:
T1 value1; // value of first field
T2 value2; // value of second field
public:
// the other public members are unchanged
…
};
For completeness, let's provide a partial specialization of Duo so that it can degenerate into a nonhomogeneous container holding just one field:
// tuples/duo6.hpp
// partial specialization for Duo<> with only one field
template <typename A>
struct Duo<A,void> {
public:
typedef A T1; // type of first field
typedef void T2; // type of second field
enum { N = 1 }; // number of fields
private:
T1 value1; // value of first field
public:
// constructors
Duo() : value1() {
}
Duo (T1 const & a)
: value1(a) {
}
// field access
T1& v1() {
return value1;
}
T1 const& v1() const {
return value1;
}
void v2() {
}
void v2() const {
}
…
};
Note that the v2() members aren't really meaningful in the partial specialization, but occasionally it is useful to have them for orthogonality.
21.2.2 Type of Fields
A recursive duo is not really handy compared with, say, a Trio or Quartet class that we could write. For example, to access the third value of the q4 object in the previous code, we'd have to use an expression like
q4.v2().v1()
This is hardly compact or intuitive. Fortunately, it is possible to write recursive templates that efficiently retrieve the values and types of fields in a recursive duo.
Let's first look at the code for a type function DuoT to retrieve the nth type of a recursive duo (you can find the code in tuples/duo3.hpp). The generic definition
// primary template for type of Nth field of (duo) T
template <int N, typename T>
class DuoT {
public:
typedef void ResultT; // in general, the result type is void
};
ensures that the result type is void for non-Duos. Fairly simple partial specializations take care of retrieving the types from nonrecursive Duos:
// specialization for 1st field of a plain duo
template <typename A, typename B>
class DuoT <1, Duo<A,B> > {
public:
typedef A ResultT;
};
// specialization for 2nd field of a plain duo
template <typename A, typename B>
class DuoT<2, Duo<A,B> > {
public:
typedef B ResultT;
};
With this in place, the nth type of a recursive duo, in general, is the (n-1)th type of the second field:
// specialization for Nth field of a recursive duo
template <int N, typename A, typename B, typename C>
class DuoT<N, Duo<A, Duo<B,C> > > {
public:
typedef typename DuoT<N-1, Duo<B,C> >::ResultT ResultT;
};
However, the request for the first type of a recursive duo ends the recursion:
// specialization for 1st field of a recursive duo
template <typename A, typename B, typename C>
class DuoT<1, Duo<A, Duo<B,C> > > {
public:
typedef A ResultT;
};
Note that the case for the second type of the recursive duo also needs a partial specialization to avoid ambiguity with the nonrecursive case:
// specialization for 2nd field of a recursive duo
template<typename A, typename B, typename C>
class DuoT<2, Duo<A, Duo<B, C> > > {
public:
typedef B ResultT;
};
This is certainly not the only way to implement the DuoT template. The interested reader could, for example, try to leverage the IfThenElse template (see Section 15.2.4 on page 272) to achieve an equivalent effect.
21.2.3 Value of Fields
Extracting the nth value (as an lvalue) from a recursive duo is only slightly more complex than extracting the corresponding type. The interface we intend to achieve is the form val<N>(duo). However, we need a helper class template DuoValue to implement it because only class templates can be partially specialized, and partial specialization allows us to recur to the desired value more efficiently. Here is how the val() functions delegate their task:
// tuples/duo5.hpp
#include "typeop.hpp"
// return Nth value of variable duo
template <int N, typename A, typename B>
inline
typename TypeOp<typename DuoT<N, Duo<A, B> >::ResultT>::RefT
val(Duo<A, B>& d)
{
return DuoValue<N, Duo<A, B> >::get(d);
}
// return Nth value of constant duo
template <int N, typename A, typename B>
inline
typename TypeOp<typename DuoT<N, Duo<A, B> >::ResultT>::RefConstT
val(Duo<A, B> const& d)
{
return DuoValue<N, Duo<A, B> >::get(d);
}
The DuoT template already proves itself useful to declare the return type of the val() functions. We also used the TypeOp type function developed in Section 15.2.3 on page 269 to create a reference type reliably, even if the field type is itself already a reference.
The following complete implementation of DuoValue clearly parallels our previous discussion of DuoT (the role of each element of the implementation is discussed next):
// tuples/duo4.hpp
#include "typeop.hpp"
// primary template for value of Nth field of (duo) T
template <int N, typename T>
class DuoValue {
public:
static void get(T&) { // in general, we have no value
}
static void get(T const&) {
}
};
// specialization for 1st field of a plain duo
template <typename A, typename B>
class DuoValue<1, Duo<A, B> > {
public:
static A& get(Duo<A, B> &d) {
return d.v1();
}
static A const& get(Duo<A, B> const &d) {
return d.v1();
}
};
// specialization for 2nd field of a plain duo
template <typename A, typename B>
class DuoValue<2, Duo<A, B> > {
public:
static B& get(Duo<A, B> &d) {
return d.v2();
}
static B const& get(Duo<A, B> const &d) {
return d.v2();
}
};
// specialization for Nth field of recursive duo
template <int N, typename A, typename B, typename C>
struct DuoValue<N, Duo<A, Duo<B,C> > > {
static
typename TypeOp<typename DuoT<N-1, Duo<B,C> >::ResultT>::RefT
get(Duo<A, Duo<B,C> > &d) {
return DuoValue<N-1, Duo<B,C> >::get(d.v2());
}
static typename TypeOp<typename DuoT<N-1, Duo<B,C>
>::ResultT>::RefConstT
get(Duo<A, Duo<B,C> > const &d) {
return DuoValue<N-1, Duo<B,C> >::get(d.v2());
}
};
// specialization for 1st field of recursive duo
template <typename A, typename B, typename C>
class DuoValue<1, Duo<A, Duo<B,C> > > {
public:
static A& get(Duo<A, Duo<B,C> > &d) {
return d.v1();
}
static A const& get(Duo<A, Duo<B,C> > const &d) {
return d.v1();
}
};
// specialization for 2nd field of recursive duo
template <typename A, typename B, typename C>
class DuoValue<2, Duo<A, Duo<B,C> > > {
public:
static B& get(Duo<A, Duo<B,C> > &d) {
return d.v2().v1();
}
static B const& get(Duo<A, Duo<B,C> > const &d) {
return d.v2().v1();
}
};
As with DuoT, we provide a generic definition of DuoValue that maps to functions that return void. Because function templates can return void expressions, this makes the application of val() to nonduos or out-of-range values of N valid (although useless, but it can simplify the implementation of certain templates):
// primary template for value of Nth field of (duo) T
template <int N, typename T>
class DuoValue {
public:
static void get(T&) { // in general, we have no value
}
static void get(T const&) {
}
};
As before, we first specialize for nonrecursive duos:
// specialization for 1st field of a plain duo
template <typename A, typename B>
class DuoValue<1, Duo<A, B> > {
public:
static A& get(Duo<A, B> &d) {
return d.v1();
}
static A const& get(Duo<A, B> const& d) {
return d.v1();
}
};
…
Then we specialize for recursive duos (again DuoT comes in handy):
template <int N, typename A, typename B, typename C>
class DuoValue<N, Duo<A, Duo<B, C> > > {
public:
static
typename TypeOp<typename DuoT<N-1, Duo<B, C> >::ResultT>::RefT
get(Duo<A, Duo<B, C> > &d) {
return DuoValue<N-1, Duo<B, C> >::get(d.v2());
}
…
};
// specialization for 1st field of recursive duo
template <typename A, typename B, typename C>
class DuoValue<1, Duo<A, Duo<B, C> > > {
public:
static A& get(Duo<A, Duo<B, C> > &d) {
return d.v1();
}
…
};
// specialization for 2nd field of recursive duo
template <typename A, typename B, typename C>
class DuoValue<2, Duo<A, Duo<B, C> > > {
public:
static B& get(Duo<A, Duo<B, C> > &d) {
return d.v2().v1();
}
…
};
The following program shows how to use duos:
// tuples/duo5.cpp
#include "duo1.hpp"
#include "duo2.hpp"
#include "duo3.hpp"
#include "duo4.hpp"
#include "duo5.hpp"
#include <iostream>
int main()
{
// create and use simple duo
Duo<bool,int> d;
std::cout << d.v1() << std::endl;
std::cout << val<1>(d) << std::endl;
// create and use triple
Duo<bool,Duo<int,float> > t;
val<1>(t) = true;
val<2>(t) = 42;
val<3>(t) = 0.2;
std::cout << val<1>(t) << std::endl;
std::cout << val<2>(t) << std::endl;
std::cout << val<3>(t) << std::endl;
}
The call of
val<3>(t)
ends up in the call of
t.v2().v2()
Because the recursion is unwrapped at compile time during the template instantiation process and the functions are simple inline accessors, these facilities end up being quite efficient. A good compiler reduces this to the same code as a simple structure field access.
However, it is still cumbersome to declare and construct recursive Duo objects. The next section addresses this challenge.
|
21.3 Tuple Construction
The nested structure of recursive duos is convenient to apply template metaprogramming techniques to them. However, for a human programmer it is more pleasing to have a flat interface to this structure. To obtain this, we can define a recursive Tuple template with many parameters and have it be a derivation from a recursive duo type of appropriate size. We show the code here for tuples up to five fields, but it is not significantly harder to provide for a dozen fields or so. You can find the code in tuples/tuple1.hpp.
To allow for tuples of varying sizes, we have unused type parameters that default to a null type, NullT, which we define as a placeholder for that purpose. We use NullT rather than void because we will create parameters of that type (void cannot be a parameter type):
// type that represents unused type parameters
class NullT {
};
Tuple is defined as a template that derives from a Duo having one more type parameter with NullT defined:
// Tuple<> in general derives from Tuple<> with one more NullT
template<typename P1,
typename P2 = NullT,
typename P3 = NullT,
typename P4 = NullT,
typename P5 = NullT>
class Tuple
: public Duo<P1, typename Tuple<P2,P3,P4,P5,NullT>::BaseT> {
public:
typedef Duo<P1, typename Tuple<P2,P3,P4,P5,NullT>::BaseT>
BaseT;
// constructors:
Tuple() {}
Tuple(TypeOp<P1>::RefConstT a1,
TypeOp<P2>::RefConstT a2,
TypeOp<P3>::RefConstT a3 = NullT(),
TypeOp<P4>::RefConstT a4 = NullT(),
TypeOp<P5>::RefConstT a5 = NullT())
: BaseT(a1, Tuple<P2,P3,P4,P5,NullT>(a2,a3,a4,a5)) {
}
};
Note the shifting pattern when passing the parameters to the recursive step. Because we derive from a base type that defines member types T1 and T2, we used template parameter names of the form Pn instead of the usual Tn.
We need a partial specialization to end this recursion with the derivation from a nonrecursive duo:
// specialization to end deriving recursion
template <typename P1, typename P2>
class Tuple<P1,P2,NullT,NullT,NullT> : public Duo<P1,P2> {
public:
typedef Duo<P1,P2> BaseT;
Tuple() {}
Tuple(TypeOp<P1>::RefConstT a1,
TypeOp<P2>::RefConstT a2,
TypeOp<NullT>::RefConstT = NullT(),
TypeOp<NullT>::RefConstT = NullT(),
TypeOp<NullT>::RefConstT = NullT())
: BaseT(a1, a2) {
}
};
A declaration such as
Tuple<bool,int,float,double> t4(true,42,13,1.95583);
ends up in the hierarchy shown in Figure 21.1.
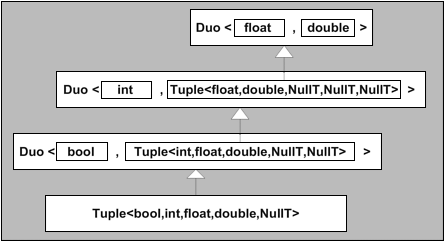
The other specialization takes care of the case when the tuple is really a singleton:
// specialization for singletons
template <typename P1>
class Tuple<P1,NullT,NullT,NullT,NullT> : public Duo<P1,void> {
public:
typedef Duo<P1,void> BaseT;
Tuple() {}
Tuple(TypeOp<P1>::RefConstT a1,
TypeOp<NullT>::RefConstT = NullT(),
TypeOp<NullT>::RefConstT = NullT(),
TypeOp<NullT>::RefConstT = NullT(),
TypeOp<NullT>::RefConstT = NullT())
: BaseT(a1) {
}
};
Finally, it is natural to desire functions like make_duo() in Section 21.1 on page 396 to deduce the template parameters automatically. Unfortunately, a different function template declaration is needed for each tuple size that must be supported because function templates cannot have default template arguments,
nor are their default function call arguments considered in the template parameter deduction process. The functions are defined as follows:
// convenience function for 1 argument
template <typename T1>
inline
Tuple<T1> make_tuple(T1 const &a1)
{
return Tuple<T1>(a1);
}
// convenience function for 2 arguments
template <typename T1, typename T2>
inline
Tuple<T1,T2> make_tuple(T1 const &a1, T2 const &a2)
{
return Tuple<T1,T2>(a1,a2);
}
// convenience function for 3 arguments
template <typename T1, typename T2, typename T3>
inline
Tuple<T1,T2,T3> make_tuple(T1 const &a1, T2 const &a2,
T3 const &a3)
{
return Tuple<T1,T2,T3>(a1,a2,a3);
}
// convenience function for 4 arguments
template <typename T1, typename T2, typename T3, typename T4>
inline
Tuple<T1,T2,T3,T4> make_tuple(T1 const &a1, T2 const &a2,
T3 const &a3, T4 const &a4)
{
return Tuple<T1,T2,T3,T4>(a1,a2,a3,a4);
}
// convenience function for 5 arguments
template <typename T1, typename T2, typename T3,
typename T4, typename T5>
inline
Tuple<T1,T2,T3,T4,T5> make_tuple(T1 const &a1, T2 const &a2,
T3 const &a3, T4 const &a4,
T5 const &a5)
{
return Tuple<T1,T2,T3,T4,T5>(a1,a2,a3,a4,a5);
}
The following program shows how to use Tuples:
// tuples/tuple1.cpp
#include "tuple1.hpp"
#include <iostream>
int main()
{
// create and use tuple with only one field
Tuple<int> t1;
val<1>(t1) += 42;
std::cout << t1.v1() << std::endl;
// create and use duo
Tuple<bool,int> t2;
std::cout << val<1>(t2) << ", ";
std::cout << t2.v1() << std::endl;
// create and use triple
Tuple<bool,int,double> t3;
val<1>(t3) = true;
val<2>(t3) = 42;
val<3>(t3) = 0.2;
std::cout << val<1>(t3) << ", ";
std::cout << val<2>(t3) << ", ";
std::cout << val<3>(t3) << std::endl;
t3 = make_tuple(false, 23, 13.13);
std::cout << val<1>(t3) << ", ";
std::cout << val<2>(t3) << ", ";
std::cout << val<3>(t3) << std::endl;
// create and use quadruple
Tuple<bool,int,float,double> t4(true,42,13,1.95583);
std::cout << val<4>(t4) << std::endl;
std::cout << t4.v2().v2().v2() << std::endl;
}
An industrial-strength implementation would complete the code we presented so far with various extensions. For example, we could define assignment operator templates to facilitate tuple conversions; otherwise, the types have to match exactly:
Tuple<bool,int,float> t3;
t3 = make_tuple(false, 23, 13.13); // ERROR: 13.13 has type double

|
21.4 Afternotes
Tuple construction is one of those template applications that appears to have been independently attempted by many programmers. The details of these attempts vary widely, but many are based on the idea of a recursive pair structure (such as our recursive duos). One interesting alternative was developed by Andrei Alexandrescu in [AlexandrescuDesign]. He cleanly separates the list of types from the list of fields in the tuple. This leads to the concept of a type list that has various applications of its own (one of which is the construction of a tuple with the encapsulated types).
Section 13.13 on page 222 discusses the concept of template list parameters, which are a language extension that makes the implementation of tuples almost trivial.
|
Chapter 22. Function Objects and Callbacks
A function object (also called a functor) is any object that can be called using the function call syntax. In the C programming language, three kinds of entities can lead to syntax that looks like a function call: functions, function-like macros, and pointers to functions. Because functions and macros are not objects, this implies that only pointers to functions are available as functors in C. In C++, additional possibilities are added: The function call operator can be overloaded for class types, a concept of references to functions exists, and member functions and pointer-to-member functions have a call syntax of their own. Not all of these concepts are equally useful, but the combination of the concept of a functor with the compile-time parameterization offered by templates leads to powerful programming techniques.
Besides developing functor types, this chapter also delves into some usage idioms for functors. Nearly all uses end up being a form of callback: The client of a library wants that library to call back some function of the client code. The classic example is a sorting routine that needs a function to compare two elements in the set being sorted. The comparison routine is passed as a functor in this case. Traditionally, the term callback has been reserved for functors that are passed as function call arguments (as opposed to, for example, template arguments), and we maintain this tradition.
The terms function object and functor are unfortunately a little fuzzy in the sense that different members of the C++ programming community may give slightly different meanings to these terms. A common variation of the definition we have given is to include only objects of class types in the functor or function object concept; function pointers are then excluded. In addition, it is not uncommon to read or hear discussions referring to the class type of a function object as a "function object." In other words, the phrase "class of function objects so and so …" is shortened to "function objects so and so …." Although we sometimes handle this terminology somewhat sloppily in our own daily work, we have made it a point to stick to our initial definitions in this chapter.
Before digging into the use of templates to implement useful functors, we discuss some properties of function calls that motivate some of the advantages of template-based functors.

|
22.1 Direct, Indirect, and Inline Calls
Typically, when a C or C++ compiler encounters the definition of a noninline function, it generates and stores machine code for that function in an object file. It also creates a name associated with the machine code; in C, this name is typically the function name itself, but in C++ the name is usually extended with an encoding of the parameter types to allow for unique names even when a function is overloaded (the resulting name is usually called a mangled name, although the term decorated name is also used). Similarly, when the compiler encounters a call site like
f();
it generates machine code for a call to a function of that type. For most machine languages, the call instruction itself necessitates the starting address of the routine. This address can be part of the instruction (in which case the instruction is called a direct call), or it may reside somewhere in memory or in a machine register (indirect call). Almost all modern computer architectures provide both types of routine calling instructions, but (for reasons that are beyond the scope of this book) direct calls are executed more efficiently than indirect calls. In fact, as computer architectures get more sophisticated, it appears that the performance gap between direct calls and indirect calls increases. Hence, compilers generally attempt to generate a direct call instruction when possible.
In general, a compiler does not know at which address a function is located (the function could, for example, be in another translation unit). However, if the compiler knows the name of the function, it generates a direct call instruction with a dummy address. In addition, it generates an entry in the generated object file directing the linker to update that instruction to point to the address of a function with the given name. Because the linker sees the object files created from all the translation units, it knows the call sites as well as the definition sites and hence is able to patch up all the direct call sites.
Unfortunately, when the name of the function is not available, an indirect call must be used. This is usually the case for calls through pointers to functions:
void foo (void (*pf)())
{
pf(); // indirect call through pointer to function pf
}
In this example it is, in general, not possible for a compiler to know to which function the parameter pf points (after all, it is most likely different for a different invocation of foo()). Hence, the technique of having the linker match names does not work. The call destination is not known until the code is actually executed.
Although a modern computer can often execute a direct call instruction about as quickly as other common instructions (for example, an instruction to add two integers), function calls can still be a serious performance impediment. The following example shows this:
int f1(int const & r)
{
return ++(int&)r; // not reasonable, but legal
}
int f2(int const & r)
{
return r;
}
int f3()
{
return 42;
}
int foo()
{
int param = 0;
int answer = 0;
answer = f1(param);
f2(param);
f3();
return answer + param;
}
Function f1() takes a const int reference argument. Ordinarily, this means that the function does not modify the object that is passed by reference. However, if the object passed in is a modifiable value, a C++ program can legally cast away the const property and change the value of the object anyway. (You could argue that this is not reasonable; however, it is standard C++.) Function f1() does exactly this. Because of this possibility, a compiler that optimizes generated code on a perfunction basis (and most compilers do) has to assume that every function that takes references or pointers to objects may modify those objects. Note that in general a compiler sees only the declaration of a function because the definition (the implementation) is in another translation unit.
In the code example, most compilers therefore assume that f2() can modify answer too (even though it does not). In fact, the compiler cannot even assume that f3() does not modify the local variable param. Indeed, the functions f1() and f2() had an opportunity to store the address of param in a globally accessible pointer. From the limited perspective of the compiler, it is therefore not impossible for f3() to use such a globally accessible pointer to modify param. The net effect is that ordinary function calls confuse most compilers regarding what happened to various objects, forcing them often to store their intermediate values in main memory instead of keeping them in fast registers and preventing many optimizations that involve the movement of machine code (the function call often forms a barrier for code motion).
Advanced C++ compilation systems exist that are capable of tracking many instances of such potential aliasing (in the scope of f1(), the expression r is an alias for the object named param in the scope of foo()). However, this ability comes at a price: compilation speed, resource usage, and code reliability. Projects that otherwise build in minutes sometimes take hours or even days to be compiled (provided the necessary gigabytes of memory are available to the compiler). Furthermore, such compilation systems are typically much more complex and are therefore more often prone to generating wrong code. Even when a superoptimizing compiler generates correct code, the source code may contain unintended violations of subtle C and C++ aliasing rules.
Some of these violations are fairly harmless with ordinary optimizers, but superoptimizers may turn them into true bugs.
However, ordinary optimizers can be helped tremendously by the process of inlining. Suppose f1(), f2(), and f3() are declared inline. The compiler can then transform the code of foo() to something essentially equivalent to
int foo'()
{
int param = 0;
int answer = 0;
answer = ++(int&)param;
return answer + param;
}
which a very ordinary optimizer can turn into
int foo''()
{
return 2;
}
This illustrates that the benefit of inlining lies not only in the avoidance of executing machine code for a calling sequence but also (and often more important) in making visible to an optimizer what happens to the variables passed to the function.
What does this have to do with templates? Well, as we see later, it is sometimes possible using template-based callbacks to generate code that involves direct or even inline calls when more traditional callbacks would result in indirect calls. The savings in running time can be considerable.
|
22.2 Pointers and References to Functions
Consider the following fairly trivial definition of a function foo():
extern "C++" void foo() throw()
{
}
The type of this function ought to be "function with C++ linkage that takes no arguments, returns no value, and does not throw any exceptions." For historical reasons, the formal definition of the C++ language does not actually make the exception specification part of a function type.
However, that may change in the future. It is a good idea to make sure that when you create code in which function types must match, the exception specifications also match. Name linkage (usually for "C" and "C++") is properly a part of the type system, but some C++ implementations are a little lax in enforcing it. Specifically, they allow a pointer to a function with C linkage to be assigned to a pointer to a function with C++ linkage and vice versa. This is a consequence of the fact that, on most platforms, calling conventions for C and C++ functions are identical as far as the common subset of parameter and return types is concerned.
In most contexts, the expression foo undergoes an implicit conversion to a pointer to the function foo(). Note that foo itself does not denote the pointer, just as the expression ia after the declaration
int ia[10];
does not denote a pointer to the array (or to the first element of the array). The implicit conversion from a function (or array) to a pointer is often called decay. To illustrate this, we can write the following complete C++ program:
// functors/funcptr.cpp
#include <iostream>
#include <typeinfo>
void foo()
{
std::cout << "foo() called" << std::endl;
}
typedef void FooT(); // FooT is a function type,
// the same type as that of function foo()
int main()
{
foo(); // direct call
// print types of foo and FooT
std::cout << "Types of foo: " << typeid(foo).name()
<< '\n';
std::cout << "Types of FooT: " << typeid(FooT).name()
<< '\n';
FooT* pf = foo; // implicit conversion (decay)
pf(); // indirect call through pointer
(*pf)(); // equivalent to pf()
// print type of pf
std::cout << "Types of pf: " << typeid(pf).name()
<< '\n';
FooT& rf = foo; // no implicit conversion
rf(); // indirect call through reference
// print type of rf
std::cout << "Types of rf: " << typeid(rf).name()
<< '\n';
}
This example shows various uses of function types, including some unusual ones.
The example uses the typeid operator, which returns a static type std::type_info, for which name() shows the types of some expressions (see Section 5.6 on page 58). No type decay occurs when typeid is applied to a function type.
Here is the output produced by one of our C++ implementations:
foo() called
Types of foo: void ()
Types of FooT: void ()
foo() called
foo() called
Types of pf: FooT *
foo() called
Types of rf: void ()
As you can see, this implementation keeps typedef names in the string returned by name() (for example, FooT * instead of its expanded form void (*)()), but this is certainly not a language requirement.
This example also shows that references to functions exist as a language concept, but pointers to functions are almost always used instead (and to avoid confusion, it is probably best to keep with this use). Observe that the expression foo is in fact a so-called lvalue because it can be bound to a reference to a non-const type. However, it is not possible to modify that lvalue.
Note that the name of a pointer to a function (like pf) or the name of a reference to a function (like rf) can be used in a function call exactly like the name of a function itself. Hence, a pointer to a function is a functoran object that can be used in place of a function name in function call syntax. On the other hand, because a reference is not an object, a reference to a function is not a functor. Recall from our discussion of direct and indirect calls that behind these identical notations can be considerably different performance characteristics.
|
22.3 Pointer-to-Member Functions
To understand why a distinction is made between pointers to ordinary functions and pointers to member functions, it is useful to study the typical C++ implementation of a call to a member function. Such a call could take the form p->mf() or a close variation of this syntax. Here, p is a pointer to an object or to a subobject. It is passed in some form as a hidden parameter to mf(), where it is known as the this pointer.
The member function mf() may have been defined for the subobject pointed to by p, or it may be inherited by the subobject. For example:
class B1 {
private:
int b1;
public:
void mf1();
};
void B1::mf1()
{
std::cout << "b1="<<b1<<std::endl;
}
As a member function, mf1() expects to be called for an object of type B1. Thus, this refers to to an object of type B1.
Let's add some more code to this:
class B2 {
private:
int b2;
public:
void mf2();
};
void B1::mf2()
{
std::cout << "b2="<<b2<<std::endl;
}
The member mf2() similarly expects the hidden parameter this to point to a B2 subobject.
Now let's derive a class from both B1 and B2:
class D: public B1, public B2 {
private:
int d;
};
With this declaration, an object of type D can behave as an object of type B1 or an object of type B2. For this to work, a D object contains both a B1 subobject and a B2 subobject. On nearly all 32-bit implementations we know of today, a D object will be organized as shown in Figure 22.1. That is, if the size of the int members is 4 bytes, member b1 has the address of this, member b2 has the address of this plus 4 bytes, and member d has the address of this plus 8 bytes. Note how the B1 subobject shares its origin with the origin of the D subobject, but the B2 subobject does not.
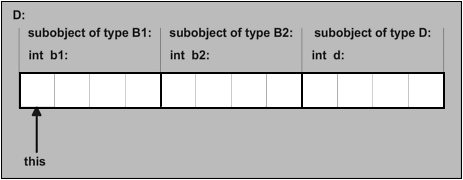
Consider now the following elementary member function calls:
int main()
{
D obj;
obj.mf1();
obj.mf2();
}
The call obj.mf2() requires the address of the subobject of type B2 in obj to be passed to mf2(). Assuming the typical implementation described, this is the address of obj plus 4 bytes. It is not at all hard for a C++ compiler to generate code to perform this adjustment. Note that for the call to mf1(), this adjustment should not be done because the address of obj is also the address of the subobject of type B1 within obj.
However, with pointer-to-member functions the compiler does not know what adjustment is needed. To see this, replace the previous main() routine with the following:
void call_memfun (D obj, void D::*pmf())
{
obj.*pmf();
}
int main()
{
D obj;
call_memfun(obj, &D::mf1);
call_memfun(obj, &D::mf2);
}
To make the situation even more opaque to a C++ compiler, the call_memfun() and main() may be placed in different translation units.
The conclusion is that in addition to the address of the function, a pointer to a member function also needs to track the this pointer adjustment needed for a particular member function. This adjustment may change when a pointer-to-member function is casted. With our example:
void D::*pmf_a() = &D::mf2; // adjustment of +4 recorded
void B2::*pmf_b() = (void (B2::*)())pmf_a; // adjustment changed to 0
The main purpose of this discussion is to illustrate the intrinsic difference between a pointer to a member function and a pointer to a function. However, the outline is not sufficient when it comes to virtual functions, and in practice many implementations use a three-word structure for pointers to member functions:
The address of the member function, or NULL if it is a virtual function The required this adjustment A virtual function index
The details are beyond the scope of this book. If you're curious about this topic, a good introduction can be found in Stan Lippman's Inside the C++ Object Model (see [LippmanObjMod]). There you will also find that pointers to data members are typically not pointers at all, but the offsets needed to get from this to a given field (a single word of storage is sufficient for their representation).
Finally, note how "getting to a member function through a pointer-to-member function" is really a binary operation involving not only the pointer but also the object to which the pointer is applied. Hence, special pointer-to-member dereferencing operators .* and ->* were introduced into the language:
obj.*pmf(… ) // call member function, to which pmf refers, for obj
ptr->*pmf(… ) // call member function, to which pmf refers, for object,
// to which ptr refers
In contrast, "getting to an ordinary function through a pointer" is a unary operation:
(*ptr)()
The dereferencing operator can be left out because it is implicit in the function call operator. The previous expression is therefore usually written as
ptr()
There is no such implicit form for pointers to member functions.

|
22.4 Class Type Functors
Although pointers to functions are functors directly available in the language, there are many situations in which it is advantageous to use a class type object with an overloaded function call operator. Doing so can lead to added flexibility, added performance, or both.
22.4.1 A First Example of Class Type Functors
Here is a very simple example of a class type functor:
// functors/functor1.cpp
#include <iostream>
// class for function objects that return constant value
class ConstantIntFunctor {
private:
int value; // value to return on ''function call''
public:
// constructor: initialize value to return
ConstantIntFunctor (int c) : value(c) {
}
// ''function call''
int operator() () const {
return value;
}
};
// client function that uses the function object
void client (ConstantIntFunctor const& cif)
{
std::cout << "calling back functor yields " << cif() << '\n';
}
int main()
{
ConstantIntFunctor seven(7);
ConstantIntFunctor fortytwo(42);
client(seven);
client(fortytwo);
}
ConstantIntFunctor is a class type from which functors can be generated. That is, if you create an object with
ConstantIntFunctor seven(7); // create function object
the expression
seven(); // call operator () for function object
is a call of operator () for the object seven rather than a call of function seven(). We achieve the same effect (indirectly) when passing the function objects seven and fortytwo through parameter cif to client().
This example illustrates what is in practice perhaps the most important advantage of class type functors over pointers to functions: the ability to associate some state (data) with the function. This is a fundamental improvement in capabilities for callback mechanisms. We can have multiple "instances" of a function with behavior that is (in a sense) parameterized.
22.4.2 Type of Class Type Functors
There is more to class type functors than the addition of state information, however. In fact, if a class type functor does not encapsulate any state, its behavior is entirely subsumed by its type, and it is sufficient to pass the type as a template argument to customize a library component's behavior.
A classic illustration of this special case includes container classes that maintain their elements in some sorted order. The sorting criterion becomes a template argument, and because it is part of the container's type, accidental mixing of containers with different sorting criteria (for example, in an assignment) is caught by the type system.
The set and map containers of the C++ standard library are parameterized this way. For example, if we define two different sets using the same element type, Person, but different sorting criteria, a comparison of the sets results in a compile-time error:
#include <set>
class Person {
…
};
class PersonSortCriterion {
public:
bool operator() (Person const& p1, Person const& p2) const {
// returns whether p1 is ''less than'' p2
…
}
};
void foo()
{
std::set<Person, std::less<Person> > c0, c1; // sort with operator <
std::set<Person, std::greater<Person> > c2; // sort with operator >
std::set<Person, PersonSortCriterion> c3; // sort with user-
… // defined criterion
c0 = c1; // OK: identical types
c1 = c2; // ERROR: different types
…
if (c1 == c3) { // ERROR: different types
…
}
}
For all three declarations of a set, the element type and the sorting criterion are passed as template arguments. The standard function object type template std::less is defined to return the result of operator < as a result of a "function call." The following simplified implementation of std::less clarifies the idea
:
namespace std {
template <typename T>
class less {
public:
bool operator() (T const& x, T const& y) const {
returnx<y;
}
};
}
The std::greater template is similar.
Because all three sorting criteria have different types, the resulting sets also have different types. Therefore, any attempt to assign or to compare two of these sets fails at compile time (the comparison operator requires the same type). This may seem straightforward, but prior to templates, the sorting criterion might have been maintained as a function pointer field of the container. Any mismatch would likely not have been detected until run time (and perhaps not without much frustrating detective work).
|
22.5 Specifying Functors
Our previous example of the standard set class shows only one way to handle the selection of functors. A number of different approaches are discussed in this section.
22.5.1 Functors as Template Type Arguments
One way to pass a functor is to make its type a template argument. A type by itself is not a functor, however, so the client function or class must create a functor object with the given type. This, of course, is possible only for class type functors, and it rules out function pointer types. A function pointer type does not by itself specify any behavior. Along the same lines of thought, this is not an appropriate mechanism to pass a class type functor that encapsulates some state information (because no particular state is encapsulated by the type alone; a specific object of that type is needed).
Here is an outline of a function template that takes a functor class type as a sorting criterion:
template <typename FO>
void my_sort (… )
{
FO cmp; // create function object
…
if (cmp(x,y)) { // use function object to compare two values
…
}
…
}
// call function with functor
my_sort<std::less<… > > (… );
With this approach, the selection of the comparison code has become a compile-time affair. And because the comparison can be "inlined," a good optimizing compiler should be able to produce code that is essentially equivalent to replacing the functor calls by direct applications of the resulting operations. To be entirely perfect, an optimizer must also be able to elide the storage used by the cmp functor object. In practice, however, only a few compilers are capable of such features.
22.5.2 Functors as Function Call Arguments
Another way to pass functors is to pass them as function call arguments. This allows the caller to construct the function object (possibly using a nontrivial constructor) at run time.
The efficiency argument is essentially similar to that of having just a functor type parameter, except that we must now copy a functor object as it is passed into the routine. This cost is usually low and can in fact be reduced to zero if the functor object has no data members (which is often the case). Indeed, consider this variation of our my_sort example:
template <typename F>
void my_sort (… , F cmp)
{
…
if (cmp(x,y)) { // use function object to compare two values
…
}
…
}
// call function with functor
my_sort (… , std::less<… >());
Within the my_sort() function, we are dealing with a copy cmp of the value passed in. When this value is an empty class object, there is no state to distinguish a locally constructed functor object from a copy passed in. Therefore, instead of actually passing the "empty functor" as a function call argument, the compiler could just use it for overload resolution and then elide the parameter/argument altogether. Inside the instantiated function, a dummy local object can then serve as the functor.
This almost works, except that the copy constructor of the "empty functor" must also be free of side effects. In practice this means that any functor with a user-defined copy constructor should not be optimized this way.
As written, the advantage of this functor specification technique is that it is also possible to pass an ordinary function pointer as argument. For example:
bool my_criterion () (T const& x, T const& y);
// call function with function object
my_sort (… , my_criterion);
Many programmers also prefer the function call syntax over the syntax involving a template type argument.
22.5.3 Combining Function Call Parameters and Template Type Parameters
It is possible to combine the two previous forms of passing functors to functions and classes by defining default function call arguments:
template <typename F>
void my_sort (… , F cmp = F())
{
…
if (cmp(x,y)) { // use function object to compare two values
…
}
…
}
bool my_criterion () (T const& x, T const& y);
// call function with functor passed as template argument
my_sort<std::less<… > > (… );
// call function with functor passed as value argument
my_sort (… , std::less<… >());
// call function with function pointer passed as value argument
my_sort (… , my_criterion);
The ordered collection classes of the C++ standard library are defined in this way: The sorting criterion can be passed as a constructor argument at run time:
class RuntimeCmp {
…
};
// pass sorting criterion as a compile-time template argument
// (uses default constructor of sorting criterion)
set<int,RuntimeCmp> c1;
// pass sorting criterion as a run-time constructor argument
set<int,RuntimeCmp> c2(RuntimeCmp(… ));
For details, see pages 178 and 197 of [JosuttisStdLib].
22.5.4 Functors as Nontype Template Arguments
Functors can also be provided through nontype template arguments. However, as mentioned in Section 4.3 on page 40 and Section 8.3.3 on page 109, a class type functor (and, in general, a class type object) is never a valid nontype template argument. For example, the following is invalid:
class MyCriterion {
public:
bool operator() (SomeType const&, SomeType const&) const;
};
template <MyCriterion F> // ERROR: MyCriterion is a class type
void my_sort (… );
However, it is possible to have a pointer or reference to a class type object as a nontype argument. This might inspire us to write the following:
class MyCriterion {
public:
virtual bool operator() (SomeType const&,
SomeType const&) const = 0;
};
class LessThan : public MyCriterion {
public:
virtual bool operator() (SomeType const&,
SomeType const&) const;
};
template<MyCriterion& F>
void sort (… );
LessThan order;
sort<order> (… ); // ERROR: requires derived-to-base
// conversion
sort<(MyCriterion&)order> (… ); // ERROR: reference nontype argument
// must be simple name
// (without a cast)
Our idea in the previous example is to capture the interface of the sorting criterion in an abstract base class type and use that type for the nontype template parameter. In an ideal world, we could then just plug in derived classes (such as LessThan) to request a specific implementation of the base class interface (MyCriterion). Unfortunately, C++ does not permit such an approach: Nontype arguments with reference or pointer types must match the parameter type exactly. An implicit derived-to-base conversion is not considered, and making the conversion explicit also invalidates the argument.
In light of our previous examples, we conclude that class type functors are not conveniently passed as nontype template arguments. In contrast, pointers (and references) to functions can be valid nontype template arguments. The following section explores some of the possibilities offered by this concept.
22.5.5 Function Pointer Encapsulation
Suppose we have a framework that expects functors like the sorting criteria of the examples in the previous sections. Furthermore, we may have some functions from an older (nontemplate) library that we'd like to act as such a functor.
To solve this problem, we can simply wrap the function call. For example:
class CriterionWrapper {
public:
bool operator() (… ) {
return wrapped_function(… );
}
};
Here, wrapped_
function() is a legacy function that we like to fit in our more general functor framework.
Often, the need to integrate legacy functions in a framework of class type functors is not an isolated event. Therefore, it can be convenient to define a template that concisely integrates such functions:
template<int (*FP)()>
class FunctionReturningIntWrapper {
public:
int operator() () {
return FP();
}
};
Here is a complete example:
// functors/funcwrap.cpp
#include <vector>
#include <iostream>
#include <cstdlib>
// wrapper for function pointers to function objects
template<int (*FP)()>
class FunctionReturningIntWrapper {
public:
int operator() () {
return FP();
}
};
// example function to wrap
int random_int()
{
return std::rand(); // call standard C function
}
// client that uses function object type as template parameter
template <typename FO>
void initialize (std::vector<int>& coll)
{
FO fo; // create function object
for (std::vector<int>::size_type i=0; i<coll.size(); ++i) {
coll[i] = fo(); // call function for function object
}
}
int main()
{
// create vector with 10 elements
std::vector<int> v(10);
// (re)initialize values with wrapped function
initialize<FunctionReturningIntWrapper<random_int> >(v);
// output elements
for (std::vector<int>::size_type i=0; i<v.size(); ++i) {
std::cout << "coll[" << i << "]: " << v[i] << std::endl;
}
}
The expression
FunctionReturningIntWrapper<random_int>
inside the call of initialize() wraps the function pointer random_int so that it can be passed as a template type parameter.
Note that we can't pass a function pointer with C linkage to this template. For example,
initialize<FunctionReturningIntWrapper<std::rand> >(v);
may not work because the std::rand() function comes from the C standard library (and may therefore have C linkage
). Instead, we can introduce a typedef for a function pointer type with the appropriate linkage:
// type for function pointer with C linkage
extern "C" typedef int (*C_int_FP)();
// wrapper for function pointers to function objects
template<C_int_FP FP>
class FunctionReturningIntWrapper {
public:
int operator() () {
return FP();
}
};
It may be worthwhile to reemphasize at this point that templates correspond to a compile-time mechanism. This means that the compiler knows which value is substituted for the nontype parameter FP of the template FunctionReturningIntWrapper. Because of this, most C++ implementations should be able to convert what at first may look like an indirect call to a direct call. Indeed, if the function were inline and its definition visible at the point of the functor invocation, it would be reasonable to expect the call to be inline.

|
22.6 Introspection
In the context of programming, the term introspection refers to the ability of a program to inspect itself. For example, in Chapter 15 we designed templates that can inspect a type and determine what kind of type it is. For functors, it is often useful to be able to tell, for example, how many arguments the functor accepts, the return type of the functor, or the nth parameter type of the functor type.
Introspection is not easily achieved for an arbitrary functor. For example, how would we write a type function that evaluates to the type of the second parameter in a functor like the following?
class SuperFunc {
public:
void operator() (int, char**);
};
Some C++ compilers provide a special type function known as typeof. It evaluates to the type of its argument expression (but doesn't actually evaluate the expression, much like the sizeof operator). With such an operator, the previous problem can be solved to a large extent, albeit not easily. The typeof concept is discussed in Section 13.8 on page 215.
Alternatively, we can develop a functor framework that requires participating functors to provide some extra information to enable some level of introspection. This is the approach we use in the remainder of this chapter.
22.6.1 Analyzing a Functor Type
In our framework, we handle only class type functors
and require them to provide the following information:
The number of parameters of the functor (as a member enumerator constant NumParams) The type of each parameter (through member typedefs Param1T, Param2T, Param3T,...) The return type of the functor (through a member typedef ReturnT)
For example, we could rewrite our PersonSortCriterion as follows to fit this framework:
class PersonSortCriterion {
public:
enum { NumParams = 2 };
typedef bool ReturnT;
typedef Person const& Param1T;
typedef Person const& Param2T;
bool operator() (Person const& p1, Person const& p2) const {
// returns whether p1 is ''less than'' p2
…
}
};
These conventions are sufficient for our purposes. They allow us to write templates to create new functors from existing ones (for example, through composition).
There are other properties of a functor that can be worth representing in this manner. For example, we could decide to encode the fact that a functor has no side effects and use this information to optimize certain generic templates. Such functors are sometimes called pure functors. It would also be useful to enable introspection of this property to enforce the need for a pure functor at compile time. For example, usually a sorting criterion should be pure
; otherwise, the results of the sorting operation could be meaningless.
22.6.2 Accessing Parameter Types
A functor can have an arbitrary number of parameters. With our conventions it is relatively straightforward to access, say, the eighth parameter type: Param8T. However, when dealing with templates it is always useful to plan for maximum flexibility. In this case, how do we write a type function that produces the Nth parameter type given the functor type and a constant N? We can do this by writing partial specializations of the following class template:
template<typename FunctorType, int N>
class FunctorParam;
We can provide partial specializations for values of N from one to some reasonably large number (say 20; functors rarely have more than 20 parameters). Each of these partial specializations can then define a member typedef Type that reflects the corresponding parameter type.
This presents one difficulty: To what should FunctorParam<F, N>::Type evaluate when N is larger than the number of parameters of the functor F? One possibility is to let such situations result in a compilation error. Although this is easily accomplished, it makes the FunctorParam type function much less useful than it could be. A second possibility is to default to type void. The disadvantage of this approach is that there are some unfortunate restrictions on type void; for example, a function cannot have a parameter type of type void, nor can we create references to void. Therefore, we opt for a third possibility: a private member class type. Objects of such a type are not easily constructed, but there are few syntactic constraints on their use. Here is an implementation of this idea:
// functors/functorparam1.hpp
#include "ifthenelse.hpp"
template <typename F, int N>
class UsedFunctorParam;
template <typename F, int N>
class FunctorParam {
private:
class Unused {
private:
class Private {};
public:
typedef Private Type;
};
public:
typedef typename IfThenElse<F::NumParams>=N,
UsedFunctorParam<F,N>,
Unused>::ResultT::Type
Type;
};
template <typename F>
class UsedFunctorParam<F, 1> {
public:
typedef typename F::Param1T Type;
};
The IfThenElse template was introduced in Section 15.2.4 on page 272. Note that we introduced a helper template UsedFunctorParam, and it is this template that needs to be partially specialized for specific values of N. A concise way to do this is to use a macro:
// functors/functorparam2.hpp
#define FunctorParamSpec(N) \
template<typename F> \
class UsedFunctorParam<F, N> { \
public: \
typedef typename F::Param##N##T Type; \
}
…
FunctorParamSpec(2);
FunctorParamSpec(3);
…
FunctorParamSpec(20);
#undef FunctorParamSpec
22.6.3 Encapsulating Function Pointers
Requiring that functor types support some introspection in the form of member typedefs excludes the use of function pointers in our framework. As discussed earlier, we can mitigate this limitation by encapsulating the function pointer. Let's develop a small tool that enables us to encapsulate functions with as many as two parameters (a larger number of parameters are handled in the same way, but let's keep the number small in the interest of clarity). We cover only the case of functions with C++ linkage; C linkage can be done in a similar way.
The solution presented here has two main components: a class template FunctionPtr with instances that are functor types encapsulating a function pointer, and an overloaded function template func_ptr() that takes a function pointer and returns a corresponding functor that fits our framework. The class template is parameterized with the return type and the parameter types:
template<typename RT, typename P1 = void, typename P2 = void>
class FunctionPtr;
Substituting a parameter with type void amounts to saying that the parameter isn't actually available. Hence, our template is able to handle multiple numbers of functor call arguments.
Because we need to encapsulate a function pointer, we need a tool to create the type of the function pointer from the parameter types. This is achieved through partial specialization as follows:
// functors/functionptrt.hpp
// primary template handles maximum number of parameters:
template<typename RT, typename P1 = void,
typename P2 = void,
typename P3 = void>
class FunctionPtrT {
public:
enum { NumParams = 3 };
typedef RT (*Type)(P1,P2,P3);
};
// partial specialization for two parameters:
template<typename RT, typename P1,
typename P2>
class FunctionPtrT<RT, P1, P2, void> {
public:
enum { NumParams = 2 };
typedef RT (*Type)(P1,P2);
};
// partial specialization for one parameter:
template<typename RT, typename P1>
class FunctionPtrT<RT, P1, void, void> {
public:
enum { NumParams = 1 };
typedef RT (*Type)(P1);
};
// partial specialization for no parameters:
template<typename RT>
class FunctionPtrT<RT, void, void, void> {
public:
enum { NumParams = 0 };
typedef RT (*Type)();
};
Notice how we used the same template to "count" the number of parameters.
The functor type we are developing passes its parameters to the function pointer it encapsulates. Passing a function call argument can have side effects: If the corresponding parameter has a class type (and not a reference to a class type), its copy constructor is invoked. To avoid this extra cost, it is useful to have a type function that leaves its argument type unchanged, except if it is a class type, in which case a reference to the corresponding const class type is produced. With the TypeT template developed in Chapter 15 and our IfThenElse utility template, this is achieved fairly concisely:
// functors/forwardparam.hpp
#ifndef FORWARD_HPP
#define FORWARD_HPP
#include "ifthenelse.hpp"
#include "typet.hpp"
#include "typeop.hpp"
// ForwardParamT<T>::Type is
// - constant reference for class types
// - plain type for almost all other types
// - a dummy type (Unused) for type void
template<typename T>
class ForwardParamT {
public:
typedef typename IfThenElse<TypeT<T>::IsClassT,
typename TypeOp<T>::RefConstT,
typename TypeOp<T>::ArgT
>::ResultT
Type;
};
template<>
class ForwardParamT<void> {
private:
class Unused {};
public:
typedef Unused Type;
};
#endif // FORWARD_HPP
Note the similarity of this template with the RParam template developed in Section 15.3.1 on page 276. The difference is that we need to map the type void (which, as mentioned earlier, is used to denote an unused parameter type) to a type that can validly appear as a parameter type.
We are now ready to define the FunctionPtr template. Because we don't know a priori how many parameters it will take, we overload the function call operator for every number of parameters (up to three in our case):
// functors/functionptr.hpp
#include "forwardparam.hpp"
#include "functionptrt.hpp"
template<typename RT, typename P1 = void,
typename P2 = void,
typename P3 = void>
class FunctionPtr {
private:
typedef typename FunctionPtrT<RT,P1,P2,P3>::Type FuncPtr;
// the encapsulated pointer:
FuncPtr fptr;
public:
// to fit in our framework:
enum { NumParams = FunctionPtrT<RT,P1,P2,P3>::NumParams };
typedef RT ReturnT;
typedef P1 Param1T;
typedef P2 Param2T;
typedef P3 Param3T;
// constructor:
FunctionPtr(FuncPtr ptr)
: fptr(ptr) {
}
// ''function calls'':
RT operator()() {
return fptr();
}
RT operator()(typename ForwardParamT<P1>::Type a1) {
return fptr(a1);
}
RT operator()(typename ForwardParamT<P1>::Type a1,
typename ForwardParamT<P2>::Type a2) {
return fptr(a1, a2);
}
RT operator()(typename ForwardParamT<P1>::Type a1,
typename ForwardParamT<P2>::Type a2,
typename ForwardParamT<P2>::Type a3) {
return fptr(a1, a2, a3);
}
};
This class template works well, but using it directly can be cumbersome. A few (inline) function templates allow us to exploit the template argument deduction mechanism to alleviate this burden:
// functors/funcptr.hpp
#include "functionptr.hpp"
template<typename RT> inline
FunctionPtr<RT> func_ptr (RT (*fp)())
{
return FunctionPtr<RT>(fp);
}
template<typename RT, typename P1> inline
FunctionPtr<RT,P1> func_ptr (RT (*fp)(P1))
{
return FunctionPtr<RT,P1>(fp);
}
template<typename RT, typename P1, typename P2> inline
FunctionPtr<RT,P1,P2> func_ptr (RT (*fp)(P1,P2))
{
return FunctionPtr<RT,P1,P2>(fp);
}
template<typename RT, typename P1, typename P2, typename P3> inline
FunctionPtr<RT,P1,P2,P3> func_ptr (RT (*fp)(P1,P2,P3))
{
return FunctionPtr<RT,P1,P2,P3>(fp);
}
All there is left to do is to try the advanced template tool we just developed with the following little demonstration program:
// functors/functordemo.cpp
#include <iostream>
#include <string>
#include <typeinfo>
#include "funcptr.hpp"
double seven()
{
return 7.0;
}
std::string more()
{
return std::string("more");
}
template <typename FunctorT>
void demo (FunctorT func)
{
std::cout << "Functor returns type "
<< typeid(typename FunctorT::ReturnT).name() << '\n'
<< "Functor returns value "
<< func() << '\n';
}
int main()
{
demo(func_ptr(seven));
demo(func_ptr(more));
}

|
22.7 Function Object Composition
Let's assume we have the following two simple mathematical functors in our framework:
// functors/math1.hpp
#include <cmath>
#include <cstdlib>
class Abs {
public:
// ''function call'':
double operator() (double v) const {
return std::abs(v);
}
};
class Sine {
public:
// ''function call'':
double operator() (double a) const {
return std::sin(a);
}
};
However, the functor we really want is the one that computes the absolute value of the sine of a given angle. Writing the new functor is not hard:
class AbsSine {
public:
double operator() (double a) {
return std::abs(std::sin(a));
}
};
Nevertheless, it is inconvenient to write new declarations for every new combination of functors. Instead, we may prefer to write a functor utility that composes two other functors. In this section we develop some templates that enable us to do this. Along the way, we introduce various concepts that prove useful in the remainder of this chapter.
22.7.1 Simple Composition
Let's start with a first cut at an implementation of a composition tool:
// functors/compose1.hpp
template <typename FO1, typename FO2>
class Composer {
private:
FO1 fo1; // first/inner function object to call
FO2 fo2; // second/outer function object to call
public:
// constructor: initialize function objects
Composer (FO1 f1, FO2 f2)
: fo1(f1), fo2(f2) {
}
// ''function call'': nested call of function objects
double operator() (double v) {
return fo2(fo1(v));
}
};
Note that when describing the composition of two functions, the function that is applied first is listed first. This means that the notation Composer<Abs, Sine> corresponds to the function sin
(abs
(x
)) (note the reversal of order). To test our little template, we can use the following program:
// functors/compose1.cpp
#include <iostream>
#include "math1.hpp"
#include "compose1.hpp"
template<typename FO>
void print_values (FO fo)
{
for (int i=-2; i<3; ++i) {
std::cout << "f(" << i*0.1
<< ") = " << fo(i*0.1)
<< "\n";
}
}
int main()
{
// print sin(abs(-0.5))
std::cout << Composer<Abs,Sine>(Abs(),Sine())(0.5) << "\n\n";
// print abs() of some values
print_values(Abs());
std::cout << '\n';
// print sin() of some values
print_values(Sine());
std::cout << '\n';
// print sin(abs()) of some values
print_values(Composer<Abs, Sine>(Abs(), Sine()));
std::cout << '\n';
// print abs(sin()) of some values
print_values(Composer<Sine, Abs>(Sine(), Abs()));
}
This demonstrates the general principle, but there is room for various improvements.
A usability improvement is achieved by introducing a small inline helper function so that the template arguments for Composer may be deduced (by now, this is a rather common technique):
// functors/composeconv.hpp
template <typename FO1, typename FO2>
inline
Composer<FO1,FO2> compose (FO1 f1, FO2 f2) {
return Composer<FO1,FO2> (f1, f2);
}
With this in place, our sample program can now be rewritten as follows:
// functors/compose2.cpp
#include <iostream>
#include "math1.hpp"
#include "compose1.hpp"
#include "composeconv.hpp"
template<typename FO>
void print_values (FO fo)
{
for (int i=-2; i<3; ++i) {
std::cout << "f(" << i*0.1
<< ") = " << fo(i*0.1)
<< "\n";
}
}
int main()
{
// print sin(abs(-0.5))
std::cout << compose(Abs(),Sine())(0.5) << "\n\n";
// print abs() of some values
print_values(Abs());
std::cout << '\n';
// print sin() of some values
print_values(Sine());
std::cout << '\n';
// print sin(abs()) of some values
print_values(compose(Abs(),Sine()));
std::cout << '\n';
// print abs(sin()) of some values
print_values(compose(Sine(),Abs()));
}
Instead of
Composer<Abs, Sine>(Abs(), Sine())
we can now use the more concise
compose(Abs(), Sine())
The next refinement is driven by a desire to optimize the Composer class template itself. More specifically, we want to avoid having to allocate any space for the members functors first and second if these functors are themselves empty classes (that is, when they are stateless), which is a common special case. This may seem to be a modest savings in storage, but remember that empty classes can undergo a special optimization when passed as function call parameters. The standard technique for our purpose is the empty base class optimization (see Section 16.2 on page 289), which turns the members into base classes:
// functors/compose3.hpp
template <typename FO1, typename FO2>
class Composer : private FO1, private FO2 {
public:
// constructor: initialize function objects
Composer(FO1 f1, FO2 f2)
: FO1(f1), FO2(f2) {
}
// ''function call'': nested call of function objects
double operator() (double v) {
return FO2::operator()(FO1::operator()(v));
}
};
This approach, however, is not really commendable. It prevents us from composing a function with itself. Indeed, the call of
// print sin(sin()) of some values
print_values(compose(Sine(),Sine())); // ERROR: duplicate base class name
leads to the instantiation of Composer such that it derives twice from class Sine, which is invalid.
This duplicate base problem can be easily avoided by adding an additional level of inheritance:
// functors/compose4.hpp
template <typename C, int N>
class BaseMem : public C {
public:
BaseMem(C& c) : C(c) { }
BaseMem(C const& c) : C(c) { }
};
template <typename FO1, typename FO2>
class Composer : private BaseMem<FO1,1>,
private BaseMem<FO2,2> {
public:
// constructor: initialize function objects
Composer(FO1 f1, FO2 f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
// ''function call'': nested call of function objects
double operator() (double v) {
return BaseMem<FO2,2>::operator()
(BaseMem<FO1,1>::operator()(v));
}
};
Clearly, the latter implementation is messier than the original, but this may be an acceptable cost if it helps an optimizer realize that the resulting functor is "empty."
Interestingly, the function call operator can be declared virtual. Doing so in a functor that participates in a composition makes the function call operator of the resulting Composer object virtual too. This can lead to some strange results. We will therefore assume that the function call operator is nonvirtual in the remainder of this section.
22.7.2 Mixed Type Composition
A more crucial improvement to the simple Composer template is to allow for more flexibility in the types involved. With the previous implementation, we allow only functors that take a double value and return another double value. Life would be more elegant if we could compose any matching type of functor. For example, we should be able to compose a functor that takes an int and returns a bool with one that takes a bool and returns a double. This is a situation in which our decision to require member typedefs in functor types comes in handy.
With the conventions assumed by our framework, the composition template can be rewritten as follows:
// functors/compose5.hpp
#include "forwardparam.hpp"
template <typename C, int N>
class BaseMem : public C {
public:
BaseMem(C& c) : C(c) { }
BaseMem(C const& c) : C(c) { }
};
template <typename FO1, typename FO2>
class Composer : private BaseMem<FO1,1>,
private BaseMem<FO2,2> {
public:
// to let it fit in our framework:
enum { NumParams = FO1::NumParams };
typedef typename FO2::ReturnT ReturnT;
typedef typename FO1::Param1T Param1T;
// constructor: initialize function objects
Composer(FO1 f1, FO2 f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
// ''function call'': nested call of function objects
ReturnT operator() (typename ForwardParamT<Param1T>::Type v) {
return BaseMem<FO2,2>::operator()
(BaseMem<FO1,1>::operator()(v));
}
};
We reused the ForwardParamT template (seeSection 22.6.3 on page 440) to avoid unnecessary copies of functor call arguments.
To use the composition template with our Abs and Sine functors, they have to be rewritten to include the appropriate type information. This is done as follows:
// functors/math2.hpp
#include <cmath>
#include <cstdlib>
class Abs {
public:
// to fit in the framework:
enum { NumParams = 1 };
typedef double ReturnT;
typedef double Param1T;
// ''function call'':
double operator() (double v) const {
return std::abs(v);
}
};
class Sine {
public:
// to fit in the framework:
enum { NumParams = 1 };
typedef double ReturnT;
typedef double Param1T;
// ''function call'':
double operator() (double a) const {
return std::sin(a);
}
};
Alternatively, we can implement Abs and Sine as templates:
// functors/math3.hpp
#include <cmath>
#include <cstdlib>
template <typename T>
class Abs {
public:
// to fit in the framework:
enum { NumParams = 1 };
typedef T ReturnT;
typedef T Param1T;
// ''function call'':
T operator() (T v) const {
return std::abs(v);
}
};
template <typename T>
class Sine {
public:
// to fit in the framework:
enum { NumParams = 1 };
typedef T ReturnT;
typedef T Param1T;
// ''function call'':
T operator() (T a) const {
return std::sin(a);
}
};
With the latter approach, using these functors requires the argument types to be provided explicitly as template arguments. The following adaptation of our sample use illustrates the slightly more cumbersome syntax:
// functors/compose5.cpp
#include <iostream>
#include "math3.hpp"
#include "compose5.hpp"
#include "composeconv.hpp"
template<typename FO>
void print_values (FO fo)
{
for (int i=-2; i<3; ++i) {
std::cout << "f(" << i*0.1
<< ") = " << fo(i*0.1)
<< "\n";
}
}
int main()
{
// print sin(abs(-0.5))
std::cout << compose(Abs<double>(),Sine<double>())(0.5)
<< "\n\n";
// print abs() of some values
print_values(Abs<double>());
std::cout << '\n';
// print sin() of some values
print_values(Sine<double>());
std::cout << '\n';
// print sin(abs()) of some values
print_values(compose(Abs<double>(),Sine<double>()));
std::cout << '\n';
// print abs(sin()) of some values
print_values(compose(Sine<double>(),Abs<double>()));
std::cout << '\n';
// print sin(sin()) of some values
print_values(compose(Sine<double>(),Sine<double>()));
}
22.7.3 Reducing the Number of Parameters
So far we have looked at a simple form of functor composition where one functor takes one argument, and that argument is another functor invocation which itself has one parameter. Clearly, functors can have multiple arguments, and therefore it is useful to allow for the composition of functors with multiple parameters. In this section we discuss the implication of allowing the first argument of Composer to be a functor with multiple parameters.
If the first functor argument of Composer takes multiple arguments, the resulting Composer class must accept multiple arguments too. This means that we have to define multiple ParamNT member types and we need to provide a function call operator (operator ()) with the appropriate number of parameters. The latter problem is not as hard to solve as it may seem. Function call operators can be overloaded; hence we can just provide function call operators for every number of parameters up to a reasonably high number (an industrial-strength functor library may go as high as 20 parameters). Any attempt to call an overloaded operator with a number of parameters that does not match the number of parameters of the first composed functor results in a translation (compilation) error, which is perfectly all right. The code might look as follows:
template <typename FO1, typename FO2>
class Composer : private BaseMem<FO1,1>,
private BaseMem<FO2,2> {
public:
…
// ''function call'' for no arguments:
ReturnT operator() () {
return BaseMem<FO2,2>::operator()
(BaseMem<FO1,1>::operator()());
}
// ''function call'' for one argument:
ReturnT operator() (typename ForwardParamT<Param1T>::Type v1) {
return BaseMem<FO2,2>::operator()
(BaseMem<FO1,1>::operator()(v1));
}
// ''function call'' for two arguments:
ReturnT operator() (typename ForwardParamT<Param1T>::Type v1,
typename ForwardParamT<Param2T>::Type v2) {
return BaseMem<FO2,2>::operator()
(BaseMem<FO1,1>::operator()(v1, v2));
}
…
};
We are now left with the task of defining members Param1T, Param2T, and so on. This task is made more complicated by the fact that these types are used in the declaration of the various function call operators: These must be valid even though the composed functors do not have corresponding parameters.
For example, if we compose two single-parameter functors, we must still come up with a Param2T type that makes a valid parameter type. Preferably, this type should not accidentally match another type used in a client program. Fortunately, we already solved this problem with FunctorParam template. The Compose template can therefore be equipped with its various member typedefs as follows:
template <typename FO1, typename FO2>
class Composer : private BaseMem<FO1,1>,
private BaseMem<FO2,2> {
public:
// the return type is straightforward:
typedef typename FO2::ReturnT ReturnT;
// define Param1T, Param2T, and so on
// - use a macro to ease the replication of the parameter type construct
#define ComposeParamT(N) \
typedef typename FunctorParam<FO1, N>::Type Param##N##T
ComposeParamT(1);
ComposeParamT(2);
…
ComposeParamT(20);
#undef ComposeParamT
…
};
Finally, we need to add the Composer constructors. They take the two functors being composed, but we allow for the various combinations of const and non-const functors:
template <typename FO1, typename FO2>
class Composer : private BaseMem<FO1,1>,
private BaseMem<FO2,2> {
public:
…
// constructors:
Composer(FO1 const& f1, FO2 const& f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
Composer(FO1 const& f1, FO2& f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
Composer(FO1& f1, FO2 const& f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
Composer(FO1& f1, FO2& f2)
: BaseMem<FO1,1>(f1), BaseMem<FO2,2>(f2) {
}
…
};
With all this library code in place, a program can now use simple constructs, as illustrated in the following example:
// functors/compose6.cpp
#include <iostream>
#include "funcptr.hpp"
#include "compose6.hpp"
#include "composeconv.hpp"
double add(double a, double b)
{
return a+b;
}
double twice(double a)
{
return 2*a;
}
int main()
{
std::cout << "compute (20+7)*2: "
<< compose(func_ptr(add),func_ptr(twice))(20,7)
<< '\n';
}
These tools can still be refined in various ways. For example, it is useful to extend the compose template to handle function pointers directly (making the use of func_ptr in our last example unnecessary). However, in the interest of brevity, we prefer to leave such improvements to the interested reader.
|
22.8 Value Binders
Often, a functor with multiple parameters remains useful when one of the parameters is bound to a specific value. For example, a simple Min functor template such as
// functors/min.hpp
template <typename T>
class Min {
public:
typedef T ReturnT;
typedef T Param1T;
typedef T Param2T;
enum { NumParams = 2 };
ReturnT operator() (Param1T a, Param2T b) {
return a<b ? b : a;
}
};
can be used to build a new Clamp functor that behaves like Min with one of its parameters bound to a certain constant. The constant could be specified as a template argument or as a run-time argument. For example, we can write the new functor as follows:
// functors/clamp.hpp
template <typename T, T max_result>
class Clamp : private Min<T> {
public:
typedef T ReturnT;
typedef T Param1T;
enum { NumParams = 1 };
ReturnT operator() (Param1T a) {
return Min<T>::operator() (a, max_result);
}
};
As with composition, it is very convenient to have some template that automates the task of binding a functor parameter available, even though it doesn't take very much code to do so manually.
22.8.1 Selecting the Binding
A binder binds a particular parameter of a particular functor to a particular value. Each of these aspects can be selected at run time (using function call arguments) or at compile time (using template arguments).
For example, the following template selects everything statically (that is, at compile time):
template<typename F, int P, int V>
class BindIntStatically;
// F is the functor type
// P is the parameter to bind
// V is the value to be bound
Each of the three binding aspects (functor, bound parameter, and bound value) can instead be selected dynamically with various degrees of convenience.
Perhaps the least convenient is to make the selection of which parameter to bind dynamic. Presumably this would involve large switch statements that delegate the functor call to different calls to the underlying functor depending on a run-time value. This may, for example look as follows:
…
switch (this->param_num) {
case 1:
return F::operator()(v, p1, p2);
case 2:
return F::operator()(p1, v, p2);
case 3:
return F::operator()(p1, p2, v);
default:
return F::operator()(p1, p2); // or an error?
}
Of the three binding aspects, this is probably the one that needs to become dynamic the least. In what follows, we therefore keep this as a template parameter so that it is a static selection.
To make the selection of the functor dynamic, it is sufficient to add a constructor that accepts a functor to our binder. Similarly, we can also pass the bound value to the constructor, but this requires us to provide storage in the binder to hold the bound value. The following two helper templates can be used to hold bound values at compile time and run time respectively:
// functors/boundval.hpp
#include "typeop.hpp"
template <typename T>
class BoundVal {
private:
T value;
public:
typedef T ValueT;
BoundVal(T v) : value(v) {
}
typename TypeOp<T>::RefT get() {
return value;
}
};
template <typename T, T Val>
class StaticBoundVal {
public:
typedef T ValueT;
T get() {
return Val;
}
};
Again, we rely on the empty base class optimization (see Section 16.2 on page 289) to avoid unnecessary overhead if the functor or the bound value representation is stateless. The beginning of our Binder template design therefore looks as follows:
// functors/binder1.hpp
template <typename FO, int P, typename V>
class Binder : private FO, private V {
public:
// constructors:
Binder(FO& f): FO(f) {}
Binder(FO& f, V& v): FO(f), V(v) {}
Binder(FO& f, V const& v): FO(f), V(v) {}
Binder(FO const& f): FO(f) {}
Binder(FO const& f, V& v): FO(f), V(v) {}
Binder(FO const& f, V const& v): FO(f), V(v) {}
template<class T>
Binder(FO& f, T& v): FO(f), V(BoundVal<T>(v)) {}
template<class T>
Binder(FO& f, T const& v): FO(f), V(BoundVal<T const>(v)) {}
…
};
Note that, in addition to constructors taking instances of our helper templates, we also provide constructor templates that automatically wrap a given bound value in a BoundVal object.
22.8.2 Bound Signature
Determining the ParamNT types for the Binder template is harder than it was for the Composer template because we cannot just take over the types of the functor on which we build. Instead, because the parameter that is bound is no longer a parameter in the new functor, we must drop the corresponding ParamNT and shift the subsequent types by one position.
To keep things modular, we can introduce a separate template that performs the selective shifting operation:
// functors/binderparams.hpp
#include "ifthenelse.hpp"
template<typename F, int P>
class BinderParams {
public:
// there is one less parameter because one is bound:
enum { NumParams = F::NumParams-1 };
#define ComposeParamT(N) \
typedef typename IfThenElse<(N<P), FunctorParam<F, N>, \
FunctorParam<F, N+1> \
>::ResultT::Type \
Param##N##T
ComposeParamT(1);
ComposeParamT(2);
ComposeParamT(3);
…
#undef ComposeParamT
};
This can be used in the Binder template as follows:
// functors/binder2.hpp
template <typename FO, int P, typename V>
class Binder : private FO, private V {
public:
// there is one less parameter because one is bound:
enum { NumParams = FO::NumParams-1 };
// the return type is straightforward:
typedef typename FO::ReturnT ReturnT;
// the parameter types:
typedef BinderParams<FO, P> Params;
#define ComposeParamT(N) \
typedef typename \
ForwardParamT<typename Params::Param##N##T>::Type \
Param##N##T
ComposeParamT(1);
ComposeParamT(2);
ComposeParamT(3);
…
#undef ComposeParamT
…
};
As usual, we use the ForwardParamT template to avoid unnecessary copying of arguments.
22.8.3 Argument Selection
To complete the Binder template we are left with the problem of implementing the function call operator. As with Composer we are going to overload this operator for varying numbers of functor call arguments. However, the problem here is considerably harder than for composition because the argument to be passed to the underlying functor can be one of three different values:
Which of the three values we select depends on the value of P and the position of the argument we are selecting.
Our idea to achieve the desired result is to write a private inline member function that accepts (by reference) the three possible values but returns (still by reference) the one that is appropriate for that argument position. Because this member function depends on which argument we're selecting, we introduce it as a static member of a nested class template. This approach enables us to write a function call operator as follows (here shown for binding a four-parameter functor; others are similar):
// functors/binder3.hpp
template <typename FO, int P, typename V>
class Binder : private FO, private V {
public:
…
ReturnT operator() (Param1T v1, Param2T v2, Param3T v3) {
return FO::operator()(ArgSelect<1>::from(v1,v1,V::get()),
ArgSelect<2>::from(v1,v2,V::get()),
ArgSelect<3>::from(v2,v3,V::get()),
ArgSelect<4>::from(v3,v3,V::get()));
}
…
};
Note that for the first and last argument, only two argument values are possible: the first or last parameter of the operator, or the bound value. If A is the position of the argument in the call to the underlying functor (1 through 3 in the example), then the corresponding parameter is selected when A-P is less than zero, the bound value is selected when A-P is equal to zero, and a parameter to the left of the argument position is selected when A-P is strictly positive. This observation justifies the definition of a helper template that selects one of three types based on the sign of a nontype template argument:
// functors/signselect.hpp
#include "ifthenelse.hpp"
template <int S, typename NegT, typename ZeroT, typename PosT>
struct SignSelectT {
typedef typename
IfThenElse<(S<0),
NegT,
typename IfThenElse<(S>0),
PosT,
ZeroT
>::ResultT
>::ResultT
ResultT;
};
With this in place, we are ready to define the member class template ArgSelect:
// functors/binder4.hpp
template <typename FO, int P, typename V>
class Binder : private FO, private V {
…
private:
template<int A>
class ArgSelect {
public:
// type if we haven't passed the bound argument yet:
typedef typename TypeOp<
typename IfThenElse<(A<=Params::NumParams),
FunctorParam<Params, A>,
FunctorParam<Params, A-1>
>::ResultT::Type>::RefT
NoSkipT;
// type if we're past the bound argument:
typedef typename TypeOp<
typename IfThenElse<(A>1),
FunctorParam<Params, A-1>,
FunctorParam<Params, A>
>::ResultT::Type>::RefT
SkipT;
// type of bound argument:
typedef typename TypeOp<typename V::ValueT>::RefT BindT;
// three selection cases implemented through different classes:
class NoSkip {
public:
static NoSkipT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return arg;
}
};
class Skip {
public:
static SkipT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return prev_arg;
}
};
class Bind {
public:
static BindT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return bound_val;
}
};
// the actual selection function:
typedef typename SignSelectT<A-P, NoSkipT,
BindT, SkipT>::ResultT
ReturnT;
typedef typename SignSelectT<A-P, NoSkip,
Bind, Skip>::ResultT
SelectedT;
static ReturnT from (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return SelectedT::select (prev_arg, arg, bound_val);
}
};
};
This is admittedly among the most complicated code segments in this book. The from member function is the one called from the functor call operators. Part of the difficulty lies in the selection of the right parameter types from which the argument is selected: SkipT and NoSkipT also incorporate the convention we use for the first and last argument (that is, repeating v1 and v4 in the operator illustrated earlier). We use the TypeOp<>::RefT construct to define these types: We could just create a reference type using the & symbol, but most compilers cannot handle "references to references" yet. The selection functions themselves are rather trivial, but they were encapsulated in member types NoSkip, Skip, and Bind to dispatch statically the appropriate function easily. Because these functions are themselves simple inline forwarding functions, a good optimizing compiler should be able to "see through" it all and generate near-optimimal code. In practice, only the best optimizers available at the time of this writing perform entirely satifactorily in the performance area. However, most other compilers still do a reasonable job of optimizing uses of Binder.
Putting it all together, our complete Binder template is implemented as follows:
// functors/binder5.hpp
#include "ifthenelse.hpp"
#include "boundval.hpp"
#include "forwardparam.hpp"
#include "functorparam.hpp"
#include "binderparams.hpp"
#include "signselect.hpp"
template <typename FO, int P, typename V>
class Binder : private FO, private V {
public:
// there is one less parameter because one is bound:
enum { NumParams = FO::NumParams-1 };
// the return type is straightforward:
typedef typename FO::ReturnT ReturnT;
// the parameter types:
typedef BinderParams<FO, P> Params;
#define ComposeParamT(N) \
typedef typename \
ForwardParamT<typename Params::Param##N##T>::Type \
Param##N##T
ComposeParamT(1);
ComposeParamT(2);
ComposeParamT(3);
…
#undef ComposeParamT
// constructors:
Binder(FO& f): FO(f) {}
Binder(FO& f, V& v): FO(f), V(v) {}
Binder(FO& f, V const& v): FO(f), V(v) {}
Binder(FO const& f): FO(f) {}
Binder(FO const& f, V& v): FO(f), V(v) {}
Binder(FO const& f, V const& v): FO(f), V(v) {}
template<class T>
Binder(FO& f, T& v): FO(f), V(BoundVal<T>(v)) {}
template<class T>
Binder(FO& f, T const& v): FO(f), V(BoundVal<T const>(v)) {}
// ''function calls'':
ReturnT operator() () {
return FO::operator()(V::get());
}
ReturnT operator() (Param1T v1) {
return FO::operator()(ArgSelect<1>::from(v1,v1,V::get()),
ArgSelect<2>::from(v1,v1,V::get()));
}
ReturnT operator() (Param1T v1, Param2T v2) {
return FO::operator()(ArgSelect<1>::from(v1,v1,V::get()),
ArgSelect<2>::from(v1,v2,V::get()),
ArgSelect<3>::from(v2,v2,V::get()));
}
ReturnT operator() (Param1T v1, Param2T v2, Param3T v3) {
return FO::operator()(ArgSelect<1>::from(v1,v1,V::get()),
ArgSelect<2>::from(v1,v2,V::get()),
ArgSelect<3>::from(v2,v3,V::get()),
ArgSelect<4>::from(v3,v3,V::get()));
}
…
private:
template<int A>
class ArgSelect {
public:
// type if we haven't passed the bound argument yet:
typedef typename TypeOp<
typename IfThenElse<(A<=Params::NumParams),
FunctorParam<Params, A>,
FunctorParam<Params, A-1>
>::ResultT::Type>::RefT
NoSkipT;
// type if we're past the bound argument:
typedef typename TypeOp<
typename IfThenElse<(A>1),
FunctorParam<Params, A-1>,
FunctorParam<Params, A>
>::ResultT::Type>::RefT
SkipT;
// type of bound argument:
typedef typename TypeOp<typename V::ValueT>::RefT BindT;
// three selection cases implemented through different classes:
class NoSkip {
public:
static NoSkipT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return arg;
}
};
class Skip {
public:
static SkipT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return prev_arg;
}
};
class Bind {
public:
static BindT select (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return bound_val;
}
};
// the actual selection function:
typedef typename SignSelectT<A-P, NoSkipT,
BindT, SkipT>::ResultT
ReturnT;
typedef typename SignSelectT<A-P, NoSkip,
Bind, Skip>::ResultT
SelectedT;
static ReturnT from (SkipT prev_arg, NoSkipT arg,
BindT bound_val) {
return SelectedT::select (prev_arg, arg, bound_val);
}
};
};
22.8.4 Convenience Functions
As with the composition templates, it is useful to write function templates that make it easier to express the binding of a value to a functor parameter. The definition of such a template is made a little harder by the need to express the type of the bound value:
// functors/bindconv.hpp
#include "forwardparam.hpp"
#include "functorparam.hpp"
template <int P, // position of the bound parameter
typename FO> // functor whose parameter is bound
inline
Binder<FO,P,BoundVal<typename FunctorParam<FO,P>::Type> >
bind (FO const& fo,
typename ForwardParamT
<typename FunctorParam<FO,P>::Type>::Type val)
{
return Binder<FO,
P,
BoundVal<typename FunctorParam<FO,P>::Type>
>(fo,
BoundVal<typename FunctorParam<FO,P>::Type>(val)
);
}
The first template parameter is not deducible: It must be specified explicitly when using the bind() template. The following example illustrates this:
// functors/bindtest.cpp
#include <string>
#include <iostream>
#include "funcptr.hpp"
#include "binder5.hpp"
#include "bindconv.hpp"
bool func (std::string const& str, double d, float f)
{
std::cout << str << ": "
<< d << (d<f? "<": ">=")
<< f << '\n';
return d<f;
}
int main()
{
bool result = bind<1>(func_ptr(func), "Comparing")(1.0, 2.0);
std::cout << "bound function returned " << result << '\n';
}
It may be tempting to simplify the bind template by adding a deducible template parameter for the bound value, thereby avoiding the cumbersome expression of the type, as done here. However, this often leads to difficulties in situations like this example, in which a literal of type double (2.0) is passed to a parameter of a compatible but different type float.
It is also often convenient to be able to bind a function (passed as a function pointer) directly. The definitions of the resulting bindfp() templates is only slightly more complicated than that of the bind template. Here is the code for the case of a function with two parameters:
// functors/bindfp2.hpp
// convenience function to bind a function pointer with two parameters
template<int PNum, typename RT, typename P1, typename P2>
inline
Binder<FunctionPtr<RT,P1,P2>,
PNum,
BoundVal<typename FunctorParam<FunctionPtr<RT,P1,P2>,
PNum
>::Type
>
>
bindfp (RT (*fp)(P1,P2),
typename ForwardParamT
<typename FunctorParam<FunctionPtr<RT,P1,P2>,
PNum
>::Type
>::Type val)
{
return Binder<FunctionPtr<RT,P1,P2>,
PNum,
BoundVal
<typename FunctorParam<FunctionPtr<RT,P1,P2>,
PNum
>::Type
>
>(func_ptr(fp),
BoundVal<typename FunctorParam
<FunctionPtr<RT,P1,P2>,
PNum
>::Type
>(val)
);
}

|
Functor Operations: A Complete Implementation
To illustrate the overall effect achieved by our sophisticated treatment of functor composition and value binding, we provide here a complete implementation of these operations for functors with up to three parameters. (It is straightforward to extend this to a dozen parameters or so, but we prefer to keep the printed code relatively concise.)
Let's first look at some sample client code:
// functors/functorops.cpp
#include <iostream>
#include <string>
#include <typeinfo>
#include "functorops.hpp"
bool compare (std::string debugstr, double v1, float v2)
{
if (debugstr != "") {
std::cout << debugstr << ": " << v1
<< (v1<v2? '<' : '>')
<< v2 << '\n';
}
return v1<v2;
}
void print_name_value (std::string name, double value)
{
std::cout << name << ": " << value << '\n';
}
double sub (double a, double b)
{
return a-b;
}
double twice (double a)
{
return 2*a;
}
int main()
{
using std::cout;
// demonstrate composition:
cout << "Composition result: "
<< compose(func_ptr(sub), func_ptr(twice))(3.0, 7.0)
<< '\n';
// demonstrate binding:
cout << "Binding result: "
<< bindfp<1>(compare, "main()->compare()")(1.02, 1.03)
<< '\n';
cout << "Binding output: ";
bindfp<1>(print_name_value,
"the ultimate answer to life")(42);
// combine composition and binding:
cout << "Mixing composition and binding (bind<1>): "
<< bind<1>(compose(func_ptr(sub),func_ptr(twice)),
7.0)(3.0)
<< '\n';
cout << "Mixing composition and binding (bind<2>): "
<< bind<2>(compose(func_ptr(sub),func_ptr(twice)),
7.0)(3.0)
<< '\n';
}
The program has the following output:
Composition result: -8
Binding result: main()->compare(): 1.02<1.03
1
Binding output: the ultimate answer to life: 42
Mixing composition and binding (bind<1>): 8
Mixing composition and binding (bind<2>): -8
The main conclusion that can be drawn from this little program is that using the functor operations developed in this section is very simple (even though implementing them was no easy task).
Note also how the binding and the composing templates interoperate seemlessly. The core facility that enables this is the small set of conventions we established for functors in Section 22.6.1 on page 436. This is not unlike the requirements established for iterators in the C++ standard library. Functors that do not follow our conventions are easily wrapped in adapter classes (as illustrated by our func_ptr() adaptation templates). Furthermore, our design allows state-of-the-art compilers to avoid any unnecessary run-time penalty compared to hand-coded functors.
Finally, the contents of functorops.hpp, which shows which header files are necessary to be able to compile the previous example, looks as follows:
// functors/functorops.hpp
#ifndef FUNCTOROPS_HPP
#define FUNCTOROPS_HPP
// define func_ptr(), FunctionPtr, and FunctionPtrT
#include "funcptr.hpp"
// define Composer<>
#include "compose6.hpp"
// define convenience function compose()
#include "composeconv.hpp"
// define Binder<>
// - includes boundval.hpp to define BoundVal<> and StaticBoundVal<>
// - includes forwardparam.hpp to define ForwardParamT<>
// - includes functorparam.hpp to define FunctorParam<>
// - includes binderparams.hpp to define BinderParams<>
// - includes signselect.hpp to define SignSelectT<>
#include "binder5.hpp"
// define convenience functions bind() and bindfp()
#include "bindconv.hpp"
#include "bindfp1.hpp"
#include "bindfp2.hpp"
#include "bindfp3.hpp"
#endif // FUNCTOROPS_HPP

|
|
|
|
